EBSILON®Professional Online Documentation
EBSILON Professional Components / Components - General and Categories / Heat Exchanger / Component 7: Steam Turbine Condenser
In This Topic
    Component 7: Steam Turbine Condenser
    In This Topic

    Component 7: Steam Turbine Condenser

     

    Specifications

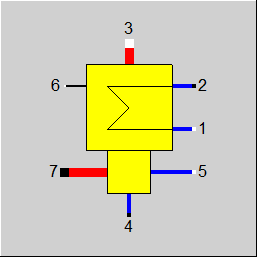
    Line connections

    1

    Cooling medium inlet

    2

    Cooling medium outlet

    3

    Exhaust steam inlet

    4

    Condensate outlet

    5

    Auxiliary condensate inlet

    6

    Control inlet for KAN or CLTUBE, Design Heat Transfer Capability or Cleanliness factor (as H)

    7

    Bypass steam outlet

     

    General       User Input Values       Characteristic Lines (if FHEI=0)       Calculation method according to HEI 6 (if FHEI=1)       Calculation method according to HEI 10 (if FHEI=10 or FHEI=-1)       Physics Used       Displays       Example

    General

    Contrary to component 10, the amount of steam to be condensed and the enthalpy of the steam have to be defined external to component 7.

    In design mode, the incoming steam pressure (as start or measurement value on line 3) and the upper terminal temperature difference (as specification value DT3S2N see Heat Exchanger General ) have to be provided. Ebsilon then calculates the cooling water flow rate M1N and the nominal value KAN for k*A (Design Heat Transfer Capability)

     In off-design mode, there are several types of calculations, which can be set by  specifying FSPEC and FHEI.

    Component 7 is expanded by the HEI 10 method. The previous HEI implementation is renamed to “HEI 6“.
    The expansion relates to the calculation of the heat transfer (k and k*A respectively) as well as of the primary pressure drop.
    Besides “HEI 6“ and “HEI 10“ it is possible to implement other HEI versions (FHEI = “user-defined“) via user-defined
    specification matrices     (see below)

    First, a differentiation must be made between normal off-design mode and the so-called identification mode.  In the normal off-design mode, it is assumed that the performance of the component (i.e. k*A as a function of other influencing parameters) is known and is either specified as a characteristic line, as an adaptation polynomial, or is given by a calculation method known as "Heat Exchange Institute" method. The pressure is calculated in such a way that complete condensation occurs.

    In identification mode the measured exhaust pressure is used to identify the component at the particular load point, i.e. to calculate k*A. If the "Heat Exchange Institute" method is chosen, the cleanliness factor of the condenser tubes will be calculated in identification mode.

    Irrespective of these different calculation modes, there are also alternatives for specifying the properties of the coolant: if the cooling water flow rate is specified, then Ebsilon calculates the cooling water outlet temperature. In case the cooling water outlet temperature is specified, Ebsilon then calculates the cooling water flow rate. The cooling water flow rate can either be specified as a start value or measurement value on line 1, or it can be assumed as fixed and specified by the specification value M1N. The flag FSPECD allows for the following design options:

    As the amount of heat to be transferred is fixed due to the specification of the steam parameters, in the first three cases the cooling water mass flow and in the latter case the outlet temperature of the cooling water is calculated.  

    Sub Cooling of the condensate is not included. However, it can be modelled by using an after-cooler (component 27).  Heat losses to the surroundings can be set with a loss factor..

    As, in practice, the condenser pressure is limited not only by the cooling water parameters but also by the evacuating system, specifying a minimum condenser pressure makes sense. This can be effected with the help of the flag FP3MIN, optionally

    As an alternative to the adaptation polynomial, an EbsScript function in the specification field EADAPT can be used (see Kernel expressions, chapter 3.2).

    When using the HEI method, a validation of the specification value for tube cleanliness (parameter CLTUBE) is possible.

     

    For more information on general notes applicable to most common heat exchangers, see Heat Exchanger General Equations, and a comparison of heat exchanger types in EBSILON can be found in the chapter Heat Exchanger General Components.

     

    Flag FSPECPD:

    In Release 13 it is possible specify the design pressure (and also the start value for the internal iteration in off-design) in the component as specification value P3N.
    The specification is controlled via the flag FSPECPD.

    Flag FDQLR

    It is possible, you can use the FDQLR flag to define how DQLR (factor for modeling heat losses) should be interpreted.

     

    External Specification of the Pressure of the Auxiliary Condensate

    Since the auxiliary condensate is at the same pressure level as the condensate, it is necessary during modeling to install a control valve or a condensate valve on the auxiliary condensate line in to decrease  the pressure to the condenser level.

    To simplify the modeling, there is now a mode “P5 given externally“ that can be set by means of the flag FP5. This mode allows to connect a line with a higher pressure on
    Pin 5. Within the component, the auxiliary condensate is then reduced to the condenser pressure. The result is the same as with an external control valve.

    This mode is the default setting for newly inserted components. For existing models, FP5 is set to “P5=P3“.

     

    Bypass mode

    The condenser also contains a flag FFU that allows to turn off the component. While in the case of other heat exchangers “turning off“ means that no heat is transferred, this is not that easily possible for the condenser as here a certain steam quantity is injected that cannot be condensed without heat dissipation. An off-state condenser therefore requires an additional outlet for the uncondensed steam (bypass steam). For this reason, a Pin 7 has been added to the condenser for the bypass steam.

    For FFU=0 (“off“) the entire incoming steam is then output unchanged (without pressure and heat loss) via this bypass. The condensate quantity is 0. There is no heat injection on the cold side. The pressure drop, however, is considered. Designing the condenser in bypass operation is not possible, and nor is specifying the cooling water outlet temperature (FSPEC=1). In bypass operation, the condenser pressure is not calculated by the condenser but has to be given externally. The specification can be effected on the bypass line, the steam feed line or the condensate line.

     

    Identification mode

    A flag FIDENT for activating the identification mode has been implemented in analogy to other components (obsolete: there was a common flag FSPEC, with which both the identification mode (P3 specification) and the cooling water specification was controlled).

     

    The flag FIDENT has the setting:

    For the cooling water specification there is a flag FSPECM with the following settings:

    To prevent the behaviour of existing models from changing, the flag FSPEC can still be used. In this case, the settings for FIDENT and FSPECM are ignored.

     

    Logic inlet (Connection point 6) for controlling component properties

    (see also : Editing components  --> Ports)

    To make component properties like efficiencies or heat transfer coefficients (variation quantity) accessible from the outside (for control or reconciliation) it is possible to place the respective value on an auxiliary line as an indexed measured value (specification value FIND). In the component, the same index must then be entered as specification value IPS.

    It is also possible to place this value on a logic line that is directly connected to the component (please see FVALKA=2, Variation variable: KAN, Dimension: Enthalpy).

    The advantage is that the allocation is graphically visible, and errors (e.g. when copying) are thus avoided.

     

    Treatment of mixtures

    As it is also possible to select mixtures (in the Refprop library) when using Component 7 with a line of the type “Two-phase fluid“, Component 7 has been upgraded to treat mixtures correctly. Previously, this feature was only available in Component 107 (Steam turbine condenser for binary mixtures).

    As this has made Component 107 redundant, it has been labeled “obsolete“. For reasons of compatibility, of course, it will remain available, so that old models can still be calculated with component 107. Possible future expansions, however, will only be implemented in Component 7, therefore the use of Component 7 is recommended.

    Please note for the case of a superheated hot fluid:

    This component assumes that the fluid to be condensed does not need to be desuperheated any more and that the impact of the desuperheating on the temperature conditions can be neglected respectively. In the case of admission of a superheated fluid, the energy balance continues to be treated correctly. However, the dew point temperature is used as the temperature relevant for Fourier’s law.

    Specifying a negative terminal temperature difference is possible, but then KAN cannot be calculated correctly any more. A warning will be output in this case. If the negative terminal temperature difference is so high that the second law of thermodynamics would be violated, an error message will be output.

    In order to achieve a more precise modeling of the condensation of a superheated fluid, the desuperheater has been upgraded for the use of binary mixtures (see Component 43).

    Universal fluid

    It is possible to use the line type Universal fluid for the fluid to be condensed too. Then, however, an admixture of auxiliary condensate is only possible if it conforms with the fluid to be condensed in terms of composition and used libraries.

     

    Note: A thermo liquid or flue gas can be used as cooling agent for the steam turbine condenser as well.

    Note about the result values:

    Performance factor RPFHX

    The quotient from the current value for k*A (result value KA) and the k*A expected in the respective load point due to the component physics and characteristic lines respectively (result value KACL) serves to assess the condition of a heat exchanger.

    The quotient KA / KACL is displayed as a result value RPFHX.

     

    Transient Modeling

    Component 7 also allows to model the turbine condenser in the transient case. The flag FINST can be used for this purpose. A thermodynamic equilibrium between the liquid and the gaseous phase in the condensate hot well is assumed.

    The transient calculation requires the specification of the geometric details of the heat exchanger.　The information on the geometry of the pipes already exists for the HEI method. In addition, the transient modeling requires the geometric details on the shell. The fluid volume, wall storage mass, and exchange surface area between wall and fluid are calculated from the geometric details. The properties of the wall material like density, thermal conductivity, and heat capacity can either be specified from the stored library (flags FMTUBE, FMSHELL) or by the user.

    The heat exchange between the fluid and the pipe wall / shell wall and the temperature development in the walls over time respectively are also considered. For this purpose, the numerical and analytical algorithm from　Component 126　is used. The combined analytic and numeric method like in comp. 119  is used for the computation of the heat exchanger wall temperature.

    For the calculation of the convective heat transfer coefficients (ALPH12, ALPH34), the user can choose between the formulae available in the VDI Heat Atlas and own specifications, also e.g. in the form of a user function (EALPH12, EALPH34).

    Having the convective heat transfer coefficients (ALPH12, ALPH34) and the heat conductivity of the tube material (LAMBDA) the value of the overall heat transfer coefficient Ktheo can be computed as

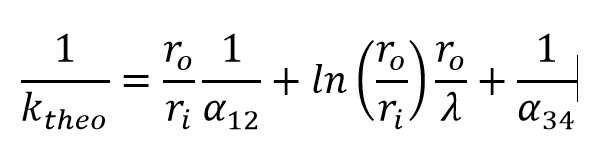
    With ro, ri being the outer and the inner tube radius respectively. From the overall heat transfer coefficient Ktheo, the heat transfer area A and the heat capacity flow W computed as the product of the mass flow m times heat capacity value CP the value of the NTU can be computed as

     

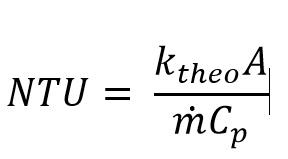
    Assuming the stirrer vessel model (VDI Heat Atlas, Edition 11, Chapter C1) for the condenser and applying the NTU-effectiveness method one can compute the heat transferred in the condenser as

     

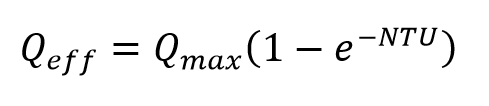
    To finally apply the Heat Exchangers Equation (5) the calculation of the heat transfer must be corrected by means of a NTU-effectiveness correction factor CORCF (value < 1) and the cleanliness factor CLTUBE as 

     

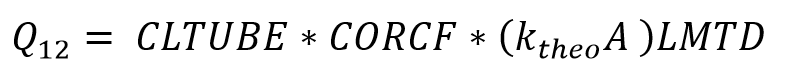
    The factor CORCF is determined in the design calculation as

     

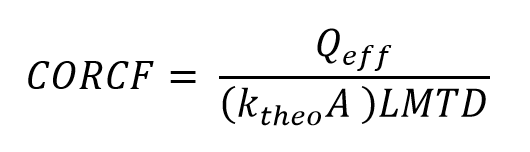
    and saved as nominal value CORCFN for the off-design calculation.

    For the steady-state solution of the heat exchange, Component 7 allows to choose between the analytical and the numerical solution (flag FALG). In the case of the numerical solution, the result depends on the number of points in flow direction (NFLOW).

    The transient mass balance considers a change of the filling level of the condensate hot well during the time step. For the mass balance, the user can decide between the specification of the filling level or of the mass flow M4 by means of the flag FSPIN. The calculated filling level is output as the volume fraction of the liquid phase of the volume between the values of VMIN and VMAX to Pin 6 as mass flow M6.

     

    The temperatures in the outer wall and inner wall and in both fluids are stored in the matrices MXTSTO and RXTSTO. The distribution of the values in the walls and in the fluids is stored in both matrices (default matrix MXTSTO for time step t-1 and result matrix RXTSTO for time step t).

    Structure of the matrices see matrices of component 7.

    The division in Y-direction in the matrix corresponds to the number NFLOW (confusing, actually the flow direction is the X-direction). Due to the fact that in BT 7 only the reduced model is used (no 2-D grid with Crank Nicolson), there is only one cell in wall normal direction (corresponds to X-direction in the matrix). Therefore, there are exactly 

    four cells in X direction: Fluid12, Bridge wall (tube wall), Fluid34, Outer wall (shell).

    User Input Values

    FINST

    Transient mode:

    0: Transient solution (time series or single calculation)

    1: Always steady state solution

    FFU

    Flag Component On / Component Off

    =0: Off (hot side bypass, cold side with pressure loss)
    =1: On

    FIDENT

    Component identification

    =0: No Identification
    =3: Identification of KA by specification the vapour pressure P3

    FSPECD

    Specification (for design)

    =0: use DT3S2N

    =1: use DT21N

    =2: T2 externally specified

    =3: M1 externally specified

    DT3S2N

    Upper terminal temperature difference (nominal) T3s-T2

    DT21N

    Cooling medium temperature rise (nominal)

    FSPECPD

    Design specification for vapour pressure

    =0:  Design vapour pressure given by specification value P3N
           (The specification value P3N is used as condenser pressure in the design case and as start value for the pressure calculation in off-design.
           If, additionally, a pressure specification is effected on the line, a double entry will be reported.)

    =1:  Design vapour pressure given externally
           (In the design case, the pressure given on the line will be used as condenser pressure and saved in P3N when the reference values are subsequently
           taken over.
           In off-design, P3N is then used as start value for the pressure calculation. If, additionally, a pressure specification is effected on the line in off-design,
           a double entry will be reported.)

    =-1: Design vapour pressure given externally (in off-design as start value)
            (The pressure given on the line is used as condenser pressure in the design case and as start value for the pressure calculation in off-design. 
            No double entry will be reported due to the specification on the line even if the pressure is defined by the condenser.
            This case corresponds to the behaviour up to Release 12.)

    P3N

    Steam pressure (nominal)

    FSPECM

    Off-design method for cooling water    

    =0: M1=M1N (constant), T2 calculated and P3 calculated (k*A used)
    =1: T2 given externally, M1 calculated und P3 calculated (k*A used)
    =2: M1 given externally, T2 calculated und P3 calculated ((k*A used)
    =3: M1 given externally, T2 validable calculated und P3 calculated ((k*A used)
    =4: like 3, with Fourier-equation LMTD*KAN-M1*(H2-H1)=0

    FDP12

    Cold side pressure drop calculation

    =0: DP12N (can also be combined with FHEI<>0)

    =1: Using HEI-method (can also be combined with FHEI=0)

    DP12N

    Cold side pressure drop line 1 to 2 (nominal)

    DP34N

    Hot side pressure drop line 3 to 4 (nominal)
    FDPNUM

    Pressure loss handling in the numerical solution

    =0: Using the average fluid pressure between inlet and outlet
    =1: Use of a linear pressure distribution between inlet and outlet, corresponding pressure values in the individual NFLOW fluid elements

    FP5

    Throttling of secondary condensate

    =0: No throttling (P5=P3)
    =1: Throttling at pin5 (P5 given externally)

    FP3MIN

    Minimal condenser pressure definition

    =0: Definition specification value (P3MIN)
    =1: Adaptation function (EP3MIN)

    P3MIN

    Minimal condenser pressure

    EP3MIN

    Adaptation function for minimal condenser pressure

    TOL

    Precision of the energy balance

    FDQLR

    Heat loss handling

    =0: Constant  (DQLR*QN in all load cases)
          DQLR refers to the design value QN (which equals the heat quantity given off by the hot flow in the design case) in all load cases, i.e. it has a constant 
          value in all load cases.
          If, however, this value exceeds 10 percent of the heat quantity given off by the hot flow, the heat loss will be limited to this value, and a warning will
          be output.
    =1: Relative to actual heat input (DQLR*Q354)
          DQLR refers to the heat quantity given off by the hot flow. If the corresponding warning is ignored, losses of more than 10 percent can be modelled
          here too.

    DQLR

    Heat loss to the environment by radiation
    (relative to the radiating current)

    FHEI

    Flag for calculation mode "Characteristic line or adaptation polynomial" or according to the "Heat Exchange Institute"

    =0: No, calculation with specified characteristic line or with adaptation polynomial
    =1: HEI 6, calculation according to the "Heat Exchange Institute" 6 method ("VDI Energietechnischen Arbeitsmappe 2000, Kapitel 8.2" )
    =10: HEI 10, calculation according to the "Heat Exchange Institute" 10th Edition
    =20: Use alpha, lambda values according to FALPH, FMTUBE specifications. The heat transfer coefficient K is computed using individual heat transfer coefficients (alpha values for cold and hot side) and lambda value for the tube material. 
    =-1: calculation according to the "Heat Exchange Institute" with user defined look-up tables

    FMODE

    Flag for calculation mode Design/Off-design

    =0: global
    =1: local off-design (i.e. always off-design mode, even if global design mode was selected)
    =2: special local off-design (special case for compatibility with earlier Ebsilon versions, should not be used in newer models, because the results of the real off-design calculations are not consistent)
    =-1: local design (d.h. always design mode, even if global off-design mode was selected)

    FFLOW

    Direction of flow (at present not used)

    FSPEC

    (deprecated)

    Flag for the setting, which parameters are specified and which have to be calculated (concerns only off-design)

    Normal calculation modes (characteristic line or adaptation polynomial / adaptation function is used):

    =0: not specified, M1=M1N, T2 and P3 calculated (using k*A)
    =1: T2 given, M1 and P3 calculated (using k*A)
    =2: M1 given, T2 and P3 calculated (using k*A)
    =6: M1 given (validable), T2 and P3 calculated (using k*A)
    =7: Like 6, with Fourier-equation LMTD*KAN-M1*(H2-H1)=0

    Identification modes (characteristic line and adaptation polynomial are ignored, k*A is calculated from measurement values):

    =3: T2 and P3 given, M1 calculated, identification of k*A or cleanliness factor CLTUBE (HEI)
    =4: P3 given, M1=M1N, identification of k*A or cleanliness factor CLTUBE (HEI)
    =5: M1 and P3 given, T2 calculated, identification of k*A or cleanliness factor CLTUBE (HEI)

    This flag is ignored in the design mode.

    The mode FSPEC=6 offers a better transfer of uncertainties ("error propagation") in validation mode by consideration of additional partial derivatives in the system of equations. Especially, a partial derivate with respect  to KAN is integrated if KAN is given externally on a logical pipe via a pseudo measurement point.

    FADAPT

    Flag for adaptation polynomial / adaptation function

    =0: Off
    =1: Correction factor for k*A [KA = KAN * char line factor (or HEI result) *polynomial]
    =2: Calculation of k*A [KA = KAN * polynomial]
    =3: Calculation of P3 [P3=P3N * polynomial]
    =1000:Not used but ADAPT evaluated as RADAPT (Reduction of the computing time)
    = -1: Correction factor for k*A [KA = KAN * char line factor (or HEI result) *adaptation function]
    = -2: Calculation of k*A [KA = KAN * adaptation function]
    = -3: Calculation of P3 [P3=P3N * adaptation function]
    = -1000: Not used, but EADAPT evaluated as RADAPT (Reduction of the computing time)

    The specified minimum pressure (P3MIN) is also adhered to in the mode FADAPT=3 and -3 respectively.

    EADAPT

    Adaptation function (input)

    FVALKA

    Validation of k*A

    =0: KAN used without validation
    =1: Deprecated: KAN used from pseudo measurement point given by IPS (can be validated)
    =2: KAN (or CLTUBE)  given by enthalpy on control inlet 6

    FTUBGEOM

    Tube geometry specification (HEI)

    =0: DTUBEIN and DTUBEOU
    =1: DTUBEIN and BWG
    =2: DTUBEOU and BWG
    =3: DTUBEIN and DWALL
    =4: DTUBEOU and DWALL

    FTUBMAT

    Tube material, selection from list  (HEI)

    0:   CuZn28Sn
    1:   SB-Cu
    2:   Aluminium
    3:   CuZn20Al
    4:   CuAl5As
    5:   Muntz metal
    6:   CuNi10Fe
    7:   CuNi30Fe
    8:   Carbon steel
    9:   X10Cr13
    10: X5CrNi189
    11: X5CrNiMo1812
    12: X8Cr17
    13: Titanium

    FTUBMAT10

    Tube material, selection from list (HEI)

    0:   Cu Fe 194
    1:   Arsenical Cu
    2:   Admirality
    3:   Al Brass
    4:   Al Bronze
    5:   Carbon Steel
    6:   Cu Ni 90-10
    7:   Cu Ni 70-30
    8:   SS (UNS S43035)
    9: Titanium Grades 1 & 2
    10:   SS (UNS S44660)
    11:   SS (UNS S44735)
    12: SS TP 304
    13: SS TP 316/317
    14: SS (UNS N08367)

    NTUBE

    Total number of tubes (HEI)

    ATUBE

    Total outer surface of tubes (HEI)

    DWALL

    Tube wall thickness (HEI)

    BWG

    Dimensionless specification of the tube wall thickness (wall gauge) in BWG (HEI)

    DTUBEIN

    Tube inner diameter (HEI)

    DTUBEOU

    Tube outer diameter (HEI)

    NPASS

    Number of water passes (HEI)

    TUBEVEL

    Averaged flow velocity in the tube HEI, Design only)

    TUBELEN

    Tube length per pass (if FDP12=1)

    CLTUBE

    Cleanliness factor (FHEI)

    IPS

    Index for pseudo measurement point

    KAN

    k*A (nominal) , Design Heat Transfer Capability

    M1N

    Primary stream  mass flow  (nominal)

    M3N

    Secondary stream mass flow (nominal)

    QN

    Generated quantity of heat at nominal load (nominal)

    AN

    Total surface area (nominal, if FHEI=10 or FHEI=-1)

    VM12N

    Primary averaged volume flow (if FHEI<>0)
    CORCFN NTU-Effectiveness correction factor (re-computed in design only)
    FALG

    Heat exchange calculation algorithm (steady state solution)

    0: analytic

    1: numeric
    FBUNDL

    Tube bundle specification

    =0: Use NTUBE, NPASS and ATUBE
    =1: Use NTUBE, NPASS and TUBELEN
    FSURF

    Surface area treatment (Design only)

    0: use given or computed ATUBE, compute CLTUBE

    1: use CLTUBE, compute AN
    FVEL

    Tube velocity treatment

    =0: UW computed from tube geometry and current volume flow
    =1: UW computed from TUBEVEL, VM12N and current volume flow
    FINIT

    Flag: Initializing state

    =0: Global, which is controlled via global variable "Transient mode" under Model Options
          "Extras" ->"Model Options" -> "Simulation" -> "Transient" -> Combo Box "Transient mode"
            (See -> Used Physics / equations -> Global Initialization of Transient Components )

    =1: First run -> Initializing while calculating steady state values
    =2: Continuation run -> Values from previous time step are input for the present ones
    SHEIG Shell height
    SLENG Shell length
    SWIDT Shell width
    SWALLT Shell wall thickness
    THISO Thickness of insulation
    FMTUBE

    Steel grade for the tubes see Material Properties of Steel

    =-1 : Properties calculated by kernel expression ERHOT, ELAMT, ECPT
    ERHOT Function for tube material density
    ELAMT Function for tube material heat conductivity
    ECPT Function for tube material heat capacity
    FMSHELL

    Steel grade for the shell see Material Properties of Steel

    =-1 : Properties calculated by kernel expression ERHOS, ELAMS, ECPS
    ERHOS Function for shell material density
    ELAMS Function for shell material heat conductivity
    ECPS Function for shell material heat capacity
    LAMISO Thermal conductivity insulation
    FALPH12

    Determination of alpha fluid12 to wall

    0: Using internal formulas from VDI Wärmeatlas Edition 11 Chapter G1

    1: from constant value AL12N

    2: from kernel expression EALPH12
    AL12N Cold side convective heat transfer coefficient (nom.)
    EALPH12 Function for ALPH12
    FALPH34

    Determination of alpha fluid34 to wall

    0: Using internal formulas from VDI Wärmeatlas Edition 11 Chapter J1

    1: from constant value AL34N

    2: from kernel expression EALPH34
    AL34N Hot side convective heat transfer coefficient (nom.)
    EALPH34 Function for ALPH34
    FALPHO

    Determination of alpha outside

    0: from specification value ALPHO

    1: from function EALPHO
    ALPHO Outer heat transfer coefficient (to ambient)
    EALPHO Function for alpha outside
    FSPIN

    Transient balance calculation mode

    0: Liquid level given, mass flows computed

    1: Mass flows given, liquid level computed
    VF Averaged liquid volume fraction (liquid level) during the time step
    VMIN Volume at liquid volume fraction 0
    VMAX Volume at liquid volume fraction 1
    FLVCALC

    Liquid volume calculation mode

    0: linear between VMIN and VMAX

    1: Using ELV
    ELV Function for the liquid volume computation
    NFLOW Number of points in flow direction (max. 100)
    FNUMSC

    Numeric scheme

    0: Upwind (highest stability)

    1: Central differences (high accuracy)
    TMIN Lower limit for storage temperature
    TMAX Upper limit for storage temperature
    FSTAMB

    Definition of ambient temperature

    0: by specification value TAMB

    1: defined by reference temperature (comp. 46)
    TAMB Ambient temperature

     

    The parameters marked in blue are reference parameters for off-design, which are calculated by Ebsilon in the design mode. The actual off-design values refer to these parameters in the equations used .

    Generally, all inputs that are visible are required. But, often default values are provided.

    For more information on colour of the input fields and their descriptions see Edit Component\Specification values

    For more information on design vs. off-design and nominal values see General\Accept Nominal values  

     

    Result value  (new Release 11)

    KOHEI                       The uncorrected heat transfer coefficient (k-value) according to the HEI method

    Characteristic Lines (if FHEI=0)

    There are two characteristic lines, which describe the effect of the primary mass flow or of the secondary mass flow respectively on k*A.

    The complete correction factor for k*A results from the multiplication of both the influencing factors.

    1st Characteristic line  CKAM1 FK1 = f (M1/M1N)
    2nd Characteristic line CKAM3 FK2 = f (M3/M3N)
     
    Total: (k*A) / KAN = FK1 * FK2
     

    These two cases have to be distinguished:

    1. One dimensional state control
    This case is characterized by the fact, that there is one M3 assigned to each M1.
    In this case you do not need to use the second characteristic line (CKAM3) - thus all values of CKAM3 or FK2 resp. have to be set to 1.0 .

    2. More complex states
    Different values of M3 are assigned to one M1.
    Here you have to use both characteristic lines (CKAM1 und CKAM3).

    Characteristic line 1:  (k*A)-Characteristic line CKAM1:  (k*A)1/(k*A)N = f (M1/M1N)

         X-Axis      1        M1/M1N                 1st point
                        2        M1/M1N                 2nd point
                        .
                        N        M1/M1N                 last point
        Y-Axis      1        (k*A)1/(k*A)N          1st point
                        2        (k*A)1/(k*A)N          2nd point
                        .
                        N        (k*A)1/(k*A)N          last poin

    Characteristic line 2:  (k*A)-Characteristic line CKAM3:  (k*A)2/(k*A)N = f (M3/M3N)

         X-Axis      1        M3/M3N                 1st point
                        2        M3/M3N                 2nd point
                        .
                        N        M3/M3N                 last point
        Y-Axis      1        (k*A)2/(k*A)N          1st point
                        2        (k*A)2/(k*A)N          2nd point
                        .
                        N        (k*A)2/(k*A)N          last point

    Specification value matrices

    MXHTCOEFF :     Heat transfer coefficient (k-value) depending on the flow velocity in the tube and on the tube diameter according to HEI 10

    MXTCORR :          Correction factor for the heat transfer coefficient depending on the cooling water inlet temperature according to HEI 10

    MSMCORR:          Correction factor for the heat transfer coefficient depending on the tube material and gauge according to HEI 10

    MXHTCOEFFUD:  Heat transfer coefficient (k-value) depending on the flow velocity in the tube and on the tube diameter – user-defined

    MXTCORRUD:      Correction factor for the heat transfer coefficient depending on the cooling water inlet temperature – user-defined

    MSMCORRUD:     Correction factor for the heat transfer coefficient depending on the tube material and gauge – user-defined

    Calculation method according to "Heat Exchange Institute 6th Edition (if FHEI=1)

    The calculation of KA is based on the method of the "Heat Exchange Institute", which is described in the "VDI Energietechnischen Arbeitsmappe 2000, Chapter 8.2".

    Calculation of KA (Heat Transfer Capability):
    KA = k * ATUBE

    Calculation of overall heat transfer coefficient k:  
    k = 6.47878 * (441.325mm-DTUBEAU)*SQRT(UW)*CT*CM*CLTUBE     in W/(m * K * mm)

    Calculation of flow velocity of the cooling water:
    UW = DX(1)/(RHOW*NTUBE*3.141592*(DTUBEIN/2)**2)  

    Calculation of specific density of the cooling water from the specific volume:
    RHOW = 1./ SPEZVOL(PX(1),TX(1))

    Correction factor for cooling water temperatures which differ from 21 °C:
    CT = 1.395-EXP(-TX(1)/22.61°C) - (TX(1)-21°C)/166°C     (for 5°C<TX(1)<40°C)

    Correction factor for pipe thickness other than 1.24 mm and raw materials other than CuZn28Sn :
    CM (as per the table given in the VDI Energietechnischen Arbeitsmappe)

    Effective cooling tube length:
    LTUBEFF = (RHOW*CPW*UW*DTUBEIN**2 ) / (4*ZW*k*DTUBEOU)
                      * LOG((TSAT(3)-TX(1))/(TSAT(3)-TX(2)))

    Calculation of the specific heat of the cooling water:
    CPW = CPW(PX(1),TX(1))

     

     

    Calculation method according to "Heat Exchange Institute 10th Edition" (if FHEI=10 or FHEI=-1)

    The calculation of KA is based on the method of the "Heat Exchange Institute", which is described in the  "HEI Steam Surface Condensers 10th Edition Chapter 4 Condenser Performance"

    Calculation of KA (Heat Transfer Capability):
    KA = k * AN


    Calculation of heat transfer coefficient k :  
    k = K0HEI*CT*CM*CLTUBE     

    The base value of k, K0HEI, is determined from the look-up matrix MXHTCOEFF (FHEI=10) or MXHTCOEFFUD (FHEI=-1) depending on the tube diameter and the flow velocity:
    K0HEI = f(DTUBEAU,TUBEVEL)  

    The correction factor for the cooling water temperature is determined from the look-up matrix MXTCORR (FHEI=10) or MXTCORRUD (FHEI=-1):
    CT = f(T1)

    The correction factor for the tube material and the wall thickness is determined from the look-up matrix MXMCORR (FHEI=10) or MXMCORRUD (FHEI=-1):
    CM = f(FTUBMAT10, DWALL or BWG)

    The primary pressure drop (FDP12=1) is computed depending on the flow velocity in the tube, the tube length per pass and the number of passes:
    DP12 = f(TUBEVEL,TUBELEN,NPASS)      
    This computation is activated using the flag FDP12 and can be used independently of FHEI flag (FDP12=1 works also if  FHEI=0)

     

    Physics Used

    Equations

    Design case (Simulation flag: GLOBAL= design case and FMODE = GLOBAL)

     

    		 P2 = P1 - DP12N                                           
    P4 = P3 - DP3N                                            
    P5 = P3                                                         

    M2 = M1                                                      
    M4 = M3 + M5                                             

    T3S = fsat (P3)
    T2 = T3S - DT3S2N
    H2 = H(P3, T3S)                                            

    T4S = fsat(P4)
    T4 = T4S
    H4 = fsat(P4)                                                 
    Q3 = M3*H3
    Q4 = M4*H4
    Q5 = M5*H5
    DQ = (Q3 + Q5 - Q4)*(1-DQLR)
    M1*(H2 - H1) = DQ                                       

    DTL = T4 - T1
    DTU = T3 - T2
    LMTD = (DTU - DTL)/(ln(DTU) - ln(DTL))

    KAN = DQ/LMTD                

    if FHEI<1, then {>

         Calculation of the cleanliness factor CLTUBE according to the method of the "Heat Exchange Institute" by specifying KA

    } 

     

    Off-design case (Simulation flag: GLOBAL = off-design or FMODE = local off-design)
      F1 = (M1/M1N) ** 2     
    P2 = P1 - DP12N * F1                                    

    F3 = (M3/M3N) ** 2
    P3 = P4 + DP34N * F3                                  
    P5 = P3                                                         

    M2 = M1                                                      
    M4 = M3 + M5                                            

    If FHEI=0, then {
      Fk1   = f (M1/M1N)  from characteristic line 1
      Fk2   = f (M3/M3N)  from characteristic line 2
            KA = KAN * Fk1 * Fk2
    }
    If FHEI<>1, then
            k / KA according to "Heat Exchange Institute"
    }

    Start ofiteration
     

    T4  = fsat(P4)
    H4  = fsat(P4)                                             
    Q12 = (Q3 + Q5 - M4*H4) * (1-DQLR)        
     

    If FSPEC = 0,2,  then {  

                        H2 = H1 + Q12/M2
                        T2 = f(P2,H2) }

    If FSPEC = 1,  then {  T2 from input }

    DTL = T4 - T1
    DTU = T3 - T2
    LMTD = (DTU - DTL)/(ln(DTU) - ln(DTL))
     
    QQ = KA * LMTD
    DQQ = Q12 - QQ
     
    Start of the Regula Falsi method
    grad = (P4- P4old)/(DQQ - DQQold)
    P4   = P4  - DQQ * grad                           
    End of the Regula Falsi method     
     
    DQ = | DQQ/((Q12+QQ)*.5) |

    If DQ < TOL, then end the iteration
                          else continue the iteration

    If FSPEC = 0,  then { M2 = M1 = M1N }                          
    If FSPEC = 1,   then {  M2 = Q12/(H2 - H1)      }           
    If FSPEC = 2,  then {  M2 = M1 from start value setter   }

    		  

    Component Displays

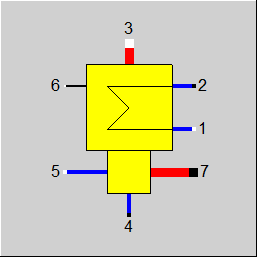    Display Option 1

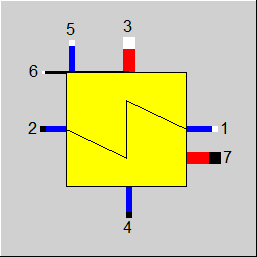    Display Option 2

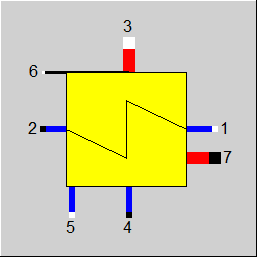    Display Option 3

    Display Option 4

    Example

    Click here >> Component 7 Demo << to load an example.

    See Also
    Heat Exchanger

     

     

    Copyright Iqony Solutions GmbH 2024 Built at 05.09.2024

    Impressum Disclaimer