Bauteil 10: Speisewasservorwärmer / Heizkondensator

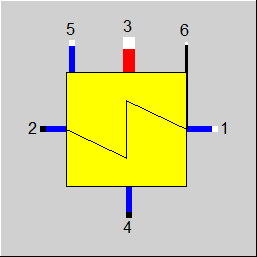
Leitungsanschlüsse

1

Eintritt (kaltes Fluid, fließt in den Rohren)

2

Austritt (kaltes Fluid, fließt in den Rohren)

3

Eintritt (warmes Fluid, fließt außerhalb der Rohre)

4

Austritt (warmes Fluid, fließt außerhalb der Rohre)

5

Nebenkondensateintritt (ohne Drossel)

6

Regeleingang für KAN (als H)

Schalter Instationaritätsmodus

0: instationäre Lösung (Zeitreihe oder Einzelberechnung)

1: immer stationäre Lösung

FMODE

Schalter für Berechnungsmodus Auslegung/Teillast

=0: global
=1: lokale Teillast (d.h. immer Teillast-Modus, auch wenn global eine Auslegungsrechnung durchgeführt wird)
=2: spezielle lokale Teillast (Sonderfall zur Kompatibilität mit früheren Ebsilon-Versionen, sollte in neuen Schaltungen nicht verwendet werden, da Ergebnisse zu echten Teillastrechnungen nicht konsistent sind)
= -1: lokale Auslegung

FFU

Schalter zum Aktivieren des Bauteils

= 1: Wärmetauscher eingeschaltet
= 0: Keine Aufwärmung des kalten Stroms. In diesem Modus wird lediglich eine Aufwärmung des Speisewassers unterbunden. Der Kondensataustritt wird aber trotzdem auf Sattwasserbedingungen gehalten. Wenn unterkühltes Nebenkondensat zugeführt wird, wird soviel Dampf gezogen, dass dieses auf Sattwassertemperatur erwärmt werden kann.

=-1: Die Dampfzufuhr wird komplett unterbunden. Wenn unterkühltes Nebenkondensat zugeführt wird, tritt dieses auch unterkühlt aus.

Der Druckverlust für die kalten Seite wird in allen Fällen gleich behandelt.

FIDENT

Komponentenidentifikation

=0:   keine Identifikation
=2:   T2 (Austrittstemperatur es kalten Stromes) von außen gegeben in Teillast, KA berechnet
=-11:nur Massen-und Energiebilanz und H4=H4'
=11: Massen-und Energiebilanz und Fourier-Gleichung LMTD*KAN-M1*(H2-H1)=0

FSPECD

Berechnungsmethode im Design-Fall

=0:   Auslegung mit DT3S2N
=1:   Auslegung mit T2-Vorgabe von außen

DT3S2N

Obere Grädigkeit T3S-T2 (Vorgabe nur im Auslegungsfall)

FDP12

Behandlung des Druckverlustes - kalte Seite

=1: Berechnung des Druckverlusts aus dem Nominalwert DP12N
=-1: P2 Druckvorgabe von außen

DP12N

Vorgabe Druckverlust 1/2 (nominal) - kalte Seite

FDP34

Behandlung des Druckverlustes - warme Seite

=1: Berechnung des Druckverlusts aus dem Nominalwert DP34N
=-1: P4 Druckvorgabe von außen

DP34N

Vorgabe Druckverlust 3/4 (nominal) - warme Seite

Druckverlusthandhabung in der numerischen Lösung

= 0: Benutzen des mittleren Fluiddruckes zwischen Ein- und Austritt
= 1: Benutzen einer linearen Druckverteilung zwischen Ein- und Austritt,  entsprechende Druckwerte in den einzelnen NFLOW Fluidelementen

Drosselung des Nebenkondensats

=0: keine Drosselung (P5=P3)
=1: Drosselung an Anschluss 5 - P5 von außen gegeben

FDQLR

Schalter für Wärmeverlust - Handhabung

=0: konstant (DQLR*QN in allen Lastfällen)
      DQLR wird in allen Lastfällen auf den Auslegungswert QN bezogen (der im Auslegungsfall gleich der vom warmen Strom abgegebenen Wärmemenge ist),    
      hat also in allen Lastfällen einen konstanten Wert.
      Wenn dieser Wert allerdings 10% der vom warmen Strom abgegebenen Wärmemenge überschreitet, wird der Wärmeverlust auf diesen Wert begrenzt und
      eine Warnung ausgegeben.

=1: relativ zum tatsächlichen Wärmeeintrag (DQLR*Q354)
      DQLR wird auf die vom warmen Strom abgegebenen Wärmemenge bezogen. Wenn man die entsprechende Warnung ignoriert, können hier auch Verluste
      von mehr als 10% modelliert werden.

DQLR

Relativer Wärmeverlust an die Umgebung

TOL

Genauigkeit der Energiebilanz für die interne Iteration

FRABEK

Berechnung nach der Methode von Rabek

=0: Nein (stattdessen Verwendung der Kennlinien)
=1: Ja (Kennlinien werden ignoriert)

FFLOW

Strömungsrichtung

=0: (zur Zeit ohne Funktion)

FSPEC
(veraltet)

= -999:  nicht verwendet (stattdessen FSPECD und FIDENT verwendet)

veralte Werte:

=0:  Austrittstemperatur T2 berechnet (im Design aus DT3S2N, in Teillast aus Fourier-Gesetz)
       Dies ist der normale Berechnungsmodus des Bauteils.

=5:  Austrittstemperatur T2 im Design von außen gegeben, in Teillast berechnet

=-1: Austrittstemperatur T2 von außen gegeben in allen Lastfällen constant (Identifikationsmodus)

=-11: Nur Berücksichtigung von Massen- und Energiebilanzen und H4 = H'. Anmerkung: Wenn diese Methode in Teillast verwendet wird, werden die Massen- und Energiebilanzen befolgt, aber der Wärmetauscher wird neu dimensioniert. Benutzen Sie diese Methode nur in geeigneten Fällen wie etwa zur Datenvalidierung. Diese Methode könnte den zweiten Hauptsatz der Thermodynamik verletzen.

=11: Nur Berücksichtigung von Massen- und Energiebilanzen und Fourier-Gleichung LMTD * KAN - M1*(H2-H1)  = 0           

FADAPT

Schalter für Verwendung des Adaptionspolynoms /  Anpassungsfunktion

=0: Nicht verwendet und nicht ausgewertet
=1: Korrekturfaktor für k*A [KA = KAN * Kennlinienfaktor *Polynom]
=2: Berechnung des k*A [KA = KA * Polynom]
=1000: Nicht verwendet, aber ADAPT ausgewertet als RADAPT (Reduzierung der Rechenzeit)
= -1: Korrekturfaktor für k*A [KA = KAN * Kennlinienfaktor * Funktion]
= -2: Berechnung des k*A [KA = KA * Funktion]
= -1000: Nicht verwendet, aber EADAPT ausgewertet als RADAPT (Reduzierung der Rechenzeit)

EADAPT

Anpassungsfunktion (Eingabe) für KA

FVALKA

Validierung von k*A

=0: KAN verwendet ohne Validierung
=1: Durch IPS bezeichnete Pseudomessstelle verwendet (validierbar)
=2: KAN auf Logikleitung 6 (Enthalpie) gegeben

IPS

Index für Pseudomessstelle

KAN                    

k*A (nominal) - Wärmeübertragungsfähigkeit im Auslegungspunkt (bei Nennlast)

M1N                    

Massenstrom kalte Seite bei Nennlast (nominal)

M3N                    

Massenstrom warme Seite bei Nennlast (nominal)

QN

Abgegebene Wärmemenge bei Nennlast (nominal)

CORCFN

NTU-Effectiveness-Korrekturfaktor bei Nennlast (nur im Designfall neu berechnet)

Geometrie-basierten Ansatz (z.B. HEI, VDI) bei Wärmeübergangsberechnung verwenden

0: Nein

1: Alpha- und Lambda-Werte gemäß FALPH und FMTUBE verwenden. Der Wärmedurchgangskoeffizient k wird aus einzelnen Wärmeübergangskoeffizienten (Alpha kalte und warme Seite) und dem Lambda-Koeffizienten der Rohre berechnet. Die Flags FALPH und FMTUBE steuern die Berechnung der Koeffizienten

Vorgabe der Rohrgeometrie

0: DTUBEIN und DTUBEOU verwenden

1: DTUBEIN und DWALL verwenden

2: DTUBEOU und DWALL verwenden

Schalter Rohrbündelvorgabe

0: NTUBE, NPASS und ATUBE verwenden

1: NTUBE, NPASS und TUBELEN verwenden

Anfangszustand

=0: GLOBAL

=1: Erster Durchlauf

=2: Folgedurchlauf

Stahlsorte der Rohre siehe Stoffeigenschaften Stahl

=-1 : Eigenschaften berechnet aus Kernelexpression ERHOT, ELAMT, ECPT

Stahlsorte des Mantelmaterials siehe Stoffeigenschaften Stahl

=-1 : Eigenschaften berechnet aus Kernelexpression ERHOS, ELAMS, ECPS

Schalter Bestimmung Alpha von Fluid 12 zur Wand

0: Gemäß Formeln VDI Wärmeatlas Auflage 11 Kapitel G1

1: aus konstantem Wert AL12N

2: aus Kernelexpression EALPH12

Bestimmung von AL34D

0: aus konstantem Wert AL34DN

1: aus AL34DN und Massenstromexponent EX34D

Schalter Bestimmung Alpha von Fluid 34 zur Wand Kondensationszone

0: Gemäß Formeln VDI Wärmeatlas Auflage 11 Kapitel J1

1: aus konstantem Wert AL34N

2: aus Kernelexpression EALPH34

Ermittlung von alpha außen

0: aus Vorgabewert ALPHO

1: aus Funktion EALPHO

Schalter Instationärer Bilanzberechnungsmodus

0: Flüssigkeitslevel gegeben, Massenströme berechnet

1: Massenströme gegeben, Flüssigkeitslevel berechnet

Berechnungsmodus für Flüssigkeitsvolumen

0: linear zwischen VMIN und VMAX

1: ELV verwenden

Numerisches Schema

0: Upwind-Verfahren (höhere Stabilität)

1: Zentral-Differenzen (höhere Genauigkeit)

Definition der Umgebungstemperatur

0: durch Vorgabewert TAMB

1: durch Referenztemperatur (Bauteil 46) definiert

Q21

Wärmemenge, um die der kalte Strom (Anschluss 1 nach Anschluss 2) erwärmt wird.

QT

 Aus dem Produkt KA * logarithmische Temperaturdifferenz berechnete Wärmemenge            

QT354

Wärmemenge, die dem Haupt- und Nebenkondensat (Summe aus Anschluss 3 und 5 nach Anschluss 4) entnommen wurde

Die Werte von Q21, QT und QT354 sollten im Rahmen der Rechengenauigkeit übereinstimmen. Differenzen deuten auf Fehler bzw. unzureichende Konvergenz hin.

KA

Berechneter Wert für das Produkt Wärmeübergangskoeffizient * effektive Wärmetauscherfläche

KANR

Verwendeter Wert für nominales KAN

KANRAB

Fiktiver Wert für den Nominalwert KAN, der bei Verwendung der Rabek-Methode zu dem Wert für k*A führen würde, der sich aktuell (aufgrund der Temperaturvorgaben) eingestellt hat.
Dieser Wert dient dazu, um einen Gütegrad des Bauteils aus Messwerten zu bestimmen. Wegen der Nichtlinearität des Rabek-Formalismus kann dies nicht einfach aus dem Verhältnis KA/KACL geschehen, sondern es muss durch Rückrechnung des Rabek-Formalismus der Wert für KAN bestimmt werden, der im aktuellen Lastfall zum durch die Messwerte bestimmten KA führt.

KANRAB wird nur berechnet, wenn

• sich das Bauteil im Identifikationsmodus befindet
  (FSPEC = "Austrittstemperatur fest gegeben" oder
  FSPEC = "Austrittstemperatur validierbar gegeben"),
• FRABEK auf "Ja" gestellt wurde,
• am Sekundäreintritt überhitzter Dampf vorliegt.

RPFHX

Gütegrad für Wärmeübergang

DTM

Mittlere logarithmische Temperaturdifferenz.
Im Gegenstrombetrieb (was bei diesem Bauteil immer der Fall ist):
DTM = ((T3S-T2)-(T4S-T1))  /  LN ((T3S-T2)/(T4S-T1))
Dabei sind T3S bzw. T4S sind die Sättigungstemperaturen zu den Drücken P3 bzw. P4.

Da bei der Berechnungsmethode nach Rabek negative Grädigkeiten auftreten können, wird hier in diesem Fall ein effektives DTM aus dem Quotienten der ausgetauschten Wärmemenge und k*A ausgegeben.

DT4S1

Untere Grädigkeit
Im Gegenstrombetrieb (was bei diesem Bauteil immer der Fall ist):
DT4S1 = T4S-T1

DT3S2

Obere Grädigkeit
Im Gegenstrombetrieb (was bei diesem Bauteil immer der Fall ist):
DT3S2 = T3S-T2

X1

Dampfgehalt Austritt kalte Seite(Anschluss 2).
Aus Gründen der Kompatibilität mit der DOS-Version wurde dieser Wert noch als Ergebniswert erhalten, inzwischen ist der Dampfgehalt auch auf der Leitung bzw. über $._2.X zugänglich.

X2

Dampfgehalt Austritt warme Seite(Anschluss 4)
Aus Gründen der Kompatibilität mit der DOS-Version wurde dieser Wert noch als Ergebniswert erhalten, inzwischen ist der Dampfgehalt auch auf der Leitung bzw. über $._4.X zugänglich.

DP12

Berechnete primärseitige Druckdifferenz
DP12 = P1 - P2

DP34

Berechnete sekundärseitige Druckdifferenz
DP34 = P3 - P4

M1M1N                   

Verhältnis des aktuellen primärseitigen Massenstroms zu seinem Nominalwert:
M1M1N = M1 / M1N

M3M3N

Verhältnis des aktuellen sekundärseitigen Massenstroms zu seinem Nominalwert:
M3M3N = M3 / M3N

KAKAN

Verhältnis des aktuellen k*A zu seinem Nominalwert:
KAKAN = KA / KAN

KACL     

Fiktiver Wert von k*A, der sich ergeben würde, wenn die Berechnung nur mit den Kennlinien erfolgen würde:

• kein Identifikationsmodus, sondern FSPEC = "Austrittstemperatur T2 berechnet"
• keine Rabek-Methode, sondern FRABEK = "Nein"
• kein Anpassungspolynom, sondern FADAPT = "Nicht verwendet"

KACL ist gleich dem Produkt aus KAN und den beiden Faktoren aus der 1/2 und 3/4 KA-Kennlinie.

RADAPT

Verwendeter Wert des Anpassungspolynoms
Dieser Wert wird nur berechnet, wenn das Anpassungspolynom auch verwendet wird, ansonsten ist er 1.

PINP

Pinchpoint
Der Pinchpoint ist definiert als die Temperaturdifferenz im Übergangspunkt zwischen Enthitzungszone und Kondensationszone:

PINP = T3S - TP

wobei TP die Temperatur des kalten Medium ist, die sich einstellt, wenn man dem kalte Medium nur die Kondensationswärme zuführt (also ohne die Wärme aus der Enthitzung). Es gilt:
HP = H1 + ((H(T3S)-H4)/(H3-H4)) * (H2-H1)
TP ist dann die aus HP und P2 mit der Wasserdampftafel berechnete Temperatur.

HSAT

Sattdampfenthalpie warme Seite

TSAT

Sättigungstemperatur warme Seite

PSAT

Sättigungsdruck warme Seite

SSAT

Sattdampfentropie warme Seite

Kennlinie 1 CKAM1 :  (k*A)-Kennlinie :  (k*A)1/(k*A)N = f (M1/M1N)

     X-Achse   1        M1/M1N                 1. Punkt
                     2        M1/M1N                 2. Punkt
                     .
                     N        M1/M1N                 letzter Punkt
     Y-Achse   1        (k*A)1/(k*A)N             1. Punkt
                      2        (k*A)1/(k*A)N             2. Punkt
                       .
                      N        (k*A)1/(k*A)N          letzter Punkt

Kennlinie 2 CKAM3 :  (k*A)-Kennlinie :  (k*A)2/(k*A)N = f (M3/M3N)

    X-Achse   1        M3/M3N                 1. Punkt
                    2        M3/M3N                 2. Punkt
                    .
                    N        M3/M3N                 letzter Punkt
     Y-Achse    1        (k*A)2/(k*A)N                    1. Punkt
                      2        (k*A)2/(k*A)N                    2. Punkt
                      .
                      N        (k*A)2/(k*A)N         letzter Punkt

Nennlastfall  (Simulationsschalter: GLOBAL=Nennlast und FMODE=GLOBAL)

T3S = f'(P3)

P2  = P1 - DP12N                                             

T2  = T3S DT3S2

H2  = f(P2,T2)

M2  = M1                                                         

Q2  = M2 * H2

DQ  = M2 * H2 - M1 * H1                                

P4  = P3 - DP34N                                            

P4  = P5                                                           

Q4  = Q3 + Q5 - DQ/(1-DQLR)

M4  = M3 + M5                                                

H4  = Q4/M4                                                    

T4  = f(P4,H4)

DTL = T4 - T1

DTU = T3 - T2

LMTD = (DTU - DTL)/(ln(DTU) - ln(DTL))
(k*A) = DQ/LMTD

M3 = (DQ/(1-DQLR)-M5*(H5-H4S))/(H3-H4S) 
 

Teillastfall (Simulationsschalter: GLOBAL = Teillast oder FMODE = lokale Teillast)

F1 = (M1/M1N) ** 2 
P2 = P1 - DP12N * F1                                             (1)
M2 = M1                                                                   (7)
Fk1 =f(M1/M1N)  aus   Kennlinie 1
Fk2 =f(M3/M3N)  aus   Kennlinie 2
(k*A) = (k*A)N * Fk1 * Fk2
F3    = (M3/M3N) ** 2 
P4    = P3 - DP34N * F3                                          (2)
P4    = P5                                                                 (3)
M4    = M3 + M5                                                       (8)

Vorabschätzung vor Beginn der Iteration
T4     = f'(P4)
H4     = f'(P4)                                                          (4)
H2max  = f(P2,T3)
Q12max = M1 * (H2max - H1)
Q34max = Q3 + Q5 - M4 * H4
Qmax   = min(Q12max,Q34max)
Q12    = 0.5* Qmax

Beginn der Iteration
H2  = H1 - Q12/M2
T2  = f (P2,H2)
DTL = T4 - T1
DTU = T3 - T2
LMTD = (DTU - DTL)/(ln(DTU) - ln(DTL))
QQ  = (k*A) * LMTD
DQQ = Q12 QQ
Start der Regula Falsi Methode
grad = (Q12 - Q12old)/(DQQ - DQQold)
Q12  = Q12 - DQQ * grad
Ende der Regula Falsi Methode 

DQ = | DQQ/((Q12+QQ)/2.0) |
Wenn DQ < TOL, dann Ende der Iteration
                      sonst Fortsetzung der Iteration

M3=(Q12+QN*DQLR-M5*(H5-H4) )/(H3-H4)        (6)
Q4  = M4 * H4 
Q12 = (Q3 + Q5 - Q4 - QN*DQLR)
Q2  = Q1 + Q12
H2  = Q2 / M2
T2  = f (P2,H2)
DQ  = M2 * H2 - M1 * H1                                       (5)

Form 1

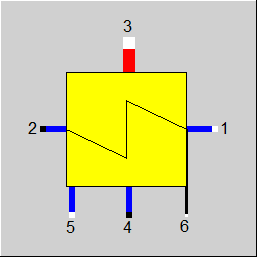Form 2