

|
Leitungsanschlüsse |
|
|
|
1 |
Eintritt Primärseite |
|
|
2 |
Austritt Primärseite |
|
|
3 |
Eintritt Sekundärseite |
|
|
4 |
Austritt Sekundärseite |
|
Allgemeines Vorgabewerte Ergebniswerte Kennlinien Verwendete Physik Bauteilform Beispiele
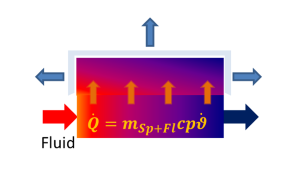
Das Bauteil 126 basiert im Wesentlichen auf dem Bauteil 119 (indirekter Speicher). Die Erweiterung besteht darin, dass ein 2. Fluid (Sekundärseite, Anschlüsse 3 & 4) in das Rechengitter eingeführt wird, welches mit dem Speicher und damit auch mit dem Fluid 1 (Primärseite, Anschlüsse 1 & 2) in thermischem Kontakt steht. Der Einfluss der Strömungsart und der Geometrie der realen Struktur auf den Wärmetransport wird durch Wärmeübergangskoeffizienten berücksichtigt. Sie werden spezifiziert für die Übergangsflächen der Fluid12-Zwischenwand-Fluid34 und Fluid34-Außenwand. Nachfolgende Abbildung verdeutlicht das dem Modell zugrunde liegende Schema.
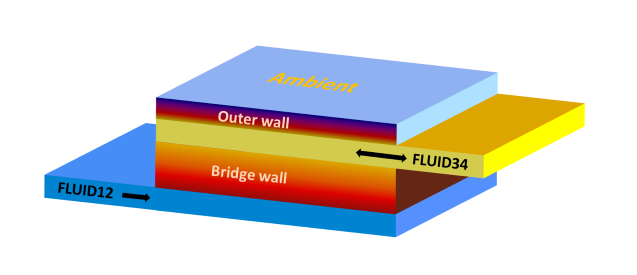 |
Eine dem Rohr äquivalente Modellierung hat den Vorzug, dass sich eine Vielzahl von technischen Anwendungen auf die Theorie des Wärmeübergangs in Rohren übertragen lässt. Ein weiterer Vorteil der Rohrgeometrie sind die kreissymmetrische Temperaturverteilung und Wärmeübertragung, so dass die Berechnung des Temperaturfelds auf eine radiale Komponente über die Querschnitte (Y-Achse des Rechengitters) und eine längs der Strömungsrichtung (X-Achse des Rechengitters) reduziert wird.
Die instationäre Wärmeleitung in der Trennwand zwischen den Fluiden sowie in der äußeren Begrenzungswand wird numerisch, analog zu Bauteil 119 mit dem Crank-Nicolson-Algorithmus berechnet. Die allgemeine Bilanzgleichung der übertragenen Wärmeströme erfährt gegenüber stationären Wärmeübertragern folgende Erweiterungen:
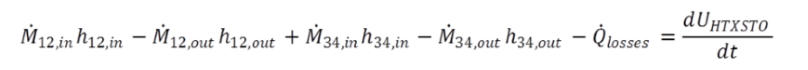 |
Nähere Erläuterungen dazu finden sich unter "Verwendete Physik/Gleichungen" 2.2.
Für t-> unendlich nähern sich die ausgetauschten Wärmemengen denen des stationären Wärmeübertragers an, damit gelten wieder die 3 charakteristischen Gleichungen für die Wärmeübertragung:
Dieses Gleichungssystem wird bei allen Berechnungen ebenfalls gelöst, damit die stationäre Lösung als Langzeitasymptote zur Verfügung steht und sich somit keine Widersprüche zu einer stationären Lösung ergeben können.
Das instationäre Bauteilverhalten wird analog zu dem Bauteil 119 über den Zeitreihendialog gesteuert.
Es gibt drei Makros (Teilmodelle), die die Verwendung dieser Komponente demonstrieren. Sie können diese in Ihr Modell einfügen, indem Sie auf den Menüeintrag "Einfügen --> Makro (Teilmodell) --> Einfügen..." klicken. Wählen Sie dann einen der Einträge "Transient heating surface", "Transient heating surface shape 2" oder "Transient heating surface shape 3". Nachdem Sie das Makro in Ihr Modell eingefügt haben, öffnen Sie das Makro, um seine Daten zu sehen. Um damit rechnen zu können, müssen noch Randwerte (Bauteile 1) an die offenen Leitungseingänge angeschlossen werden und eine Zeitreihe muss angelegt werden.
|
FMODE |
Schalter für Berechnungsmodus Auslegung/Teillast =0: wie global eingestellt =1: lokale Teillast (d.h. immer Teillast-Modus, auch wenn global eine Auslegungsrechnung durchgeführt wird) =2: spezielle lokale Teillast (Sonderfall zur Kompatibilität mit früheren Ebsilon-Versionen, sollte in neuen Schaltungen nicht verwendet werden, da Ergebnisse zu echten Teillastrechnungen nicht konsistent sind) = -1: lokale Auslegung (d.h. immer Auslegungs-Modus, auch wenn global eine Teillastrechnung durchgeführt wird) |
|
FINIT |
Schalter für Initialisierung der instationären Berechnungen =0: GLOBAL gesteuert durch die Variable "Instationärer Modus" in Modell-Einstellungen " Extras" -> "Modelleinstellungen" -> "Simulation" -> "Instationär" -> Kombobox "Instationärer Modus" |
|
FINST |
Schalter für Instationarität =0: instationäre Berechnung entsprechend der Vorgaben im Zeitreihendialog |
|
FFU |
Ein-/Aus-Schalter =0: Wärmetauscher AUS (Nur Berechnung der Druckverluste) =1: Wärmetauscher EIN |
|
AWF13 |
Wärmeübertragungsfläche Zwischenwand (Bridge wall) |
| FVOL |
Schalter für die Berücksichtigung der Abhängigkeit des Druckverlusts vom Volumen =0: ohne DP/DPN = (M/MN)**2 |
| FDPNUM |
Druckverlusthandhabung in der numerischen Lösung = 0: Benutzen des mittleren Fluiddruckes zwischen Ein- und Austritt |
|
FDP12RN |
Schalter für die Art der Vorgabe des primärseitigen Druckverlusts =1: absolut (DP12N=DP12RN) |
|
DP12RN |
Druckverlust 12 (nominal) [absolut oder relativ zu P1] |
|
FDP34RN |
Schalter für die Art der Vorgabe des sekundärseitigen Druckverlusts =1: absolut (DP34N=DP34RN) |
|
DP34RN |
Druckverlust 34 (nominal) [absolut oder relativ zu P3] |
|
FALPH12
|
Schalter für den Berechnungsmodus des primärseitigen Wärmeübergangskoeffizienten FLUID12 an den Speicher =0: immer konstanter Wert AL12N |
|
AL12N |
primärseitiger Wärmeübertragungskoeffizient (nominal, nur sichtbar wenn FALPH12 = 0|1) )
|
|
EX12 |
Massenstromexponent für die Berechnung von AL12 |
|
EALPH12 |
Funktion für die Berechnung von AL12, entspricht dem Rückgabewert evalexpr (typ real) |
|
FALPH34 |
Schalter für den Berechnungsmodus des sekundärseitigen Wärmeübergangskoeffizienten FLUID34 an den Speicher (gültig für den Wärmeübergang zur Zwischen- und Außenwand) =0: immer konstanter Wert AL34N |
|
AL34N
|
sekundärseitiger Wärmeübertragungskoeffizient (nominal, nur sichtbar wenn FALPH34 = 0|1) Als erste Annahme werden folgende Werte empfohlen:
|
|
EX34 |
Massenstromexponent für die Berechnung von AL34 |
|
EALPH34 |
Funktion für die Berechnung von AL34, entspricht dem Rückgabewert evalexpr (typ real) |
| DAL34DT | Zusätzlicher Teillast-Gradient für AL34 - siehe Bauteil 61 Die Temperaturabhängigkeit von AL34 kann damit beeinflusst werden - Standardwert bis Release 16: 0.0005 |
|
FALPHO
|
Schalter für den Berechnungsmodus des Wärmeübergangskoeffizienten der Speicher-Außenwand an die Umgebung =0: immer konstanter Wert ALPHO |
|
ALPHO |
außenseitiger Wärmeübertragungskoeffizient ( nur sichtbar wenn FALPHO = 0) |
|
EALPHO |
Funktion für die Berechnung von ALPHO, entspricht dem Rückgabewert evalexpr (typ real) |
|
THISO |
Dicke der Außenisolierung |
|
LAMISO |
Wärmeleitfähigkeit des Isoliermaterials |
|
FALGINST |
Schalter für instationären Berechnungsmodus =1: Crank-Nicolson-Algorithmus |
|
FFLOW |
Strömungsart =0: Gegenstrom |
|
TAUADBW |
Korrekturfaktor für Zeitkonstante der Zwischenwand (reduziertes physikalisches Modell) |
|
TAUADOW |
Korrekturfaktor für Zeitkonstante der Außenwand (reduziertes physikalisches Modell) |
|
LAMADJ |
Multiplikator zu 1/LAMBDA - Widerstand durch die Wärmeleitfähigkeit der Rohrwand (reduziertes physikalisches Modell) Setzen LAMADJ=0 ist äquivalent zum Vernachlässigen des Widerstands durch die Wärmeleitfähigkeit der Rohrwand: entspricht entweder einer unendlich dünnen Rohrwand oder einem unendlich hohen Lambda-Wert Setzen LAMADJ=1 is äquivalent zur Berechnung des Widerstands durch die Wärmeleitfähigkeit der Rohrwand mit den Originalwerten vom LAMBDA und von der Rohrwandstärke LAMADJ<1 führt zur Verkleinerung des Widerstands durch die Wärmeleitfähigkeit der Rohrwand LAMADJ>1 führt zur Vergrößerung des Widerstands durch die Wärmeleitfähigkeit der Rohrwand |
|
FADAPT |
Schalter für die Verwendung des Anpassungspolynoms ADAPT / Anpassungsfunktion EADAPT = 0: nicht verwendet und nicht ausgewertet |
|
EADAPT |
Eingabe der Anpassungsfunktion für KA |
|
TOLXECO |
Tolerierbarer Dampfgehalt am Economizer. Wenn der Dampfgehalt X am Austritt größer als TOLXECO ist, wird eine Warnung ausgegeben. Wenn er größer als 2*TOLXECO ist, wird eine Fehlermeldung ausgegeben. |
|
PINPMIN |
Mindestwert für den Pinchpoint (KA wird automatisch reduziert, wenn der Pinchpoint kleiner als dieser Wert wird) |
|
LSTO12 |
Strömungslänge primärseitig FLUID12 |
|
LSTO34 |
Strömungslänge sekundärseitig FLUID34 |
|
AWOUT |
Für den Wärmeaustausch relevante Fläche der Außenwand |
|
MWF13 |
Masse der Speicherwand (Bridge wall) zwischen den Fluiden 12 und 34 |
|
MWOUT |
Masse der äußeren Speicherwand |
|
FVFLUID |
Schalter für Berechnung des Fluidvolumens =0: gegeben durch die Spezwerte VFLUID12, VFLUID34 |
|
VFLUID12 |
Volumen des primärseitigen FLUID12 |
|
VFLUID34 |
Volumen des sekundärseitigen FLUID34 |
|
FDATABW |
Schalter für Berechnung der Materialparameter der Speicherzwischenwand =1: konstant aus den Vorgabewerten RHOBW, LAMBW und CPBW =2: linear interpoliert mit Hilfe von RHOBW/DRHOBW, LAMBW/DLAMBW und CPBW/DCPBW
=3: aus Kennlinien CRHOBW, CLAMBW, CCPBW |
|
RHOBW |
Dichte des Speichermaterials der Zwischenwand |
|
DRHOBW |
Änderung der Dichte des Speichermaterials mit der Temperatur |
|
LAMBW |
Wärmeleitfähigkeit des Speichermaterials der Zwischenwand |
|
DLAMBW |
Änderung der Wärmeleitfähigkeit des Speichermaterials mit der Temperatur |
|
CPBW |
Spezifische Wärmekapazität des Speichermaterials der Zwischenwand |
|
DCPBW |
Änderung der Wärmekapazität des Speichermaterials mit der Temperatur |
|
TREFBW |
Referenztemperatur für die Berechnung der Stoffdaten des Speichermaterials der Zwischenwand (relevant für FDATABW=2) |
|
FDATAOW |
Schalter für Berechnung der Materialparameter der Speicheraußenwand =1: konstant aus den Vorgabewerten RHOOW, LAMOW und CPOW
=3: aus Kennlinien CRHOOW, CLAMOW, CCPOW |
|
RHOOW |
Dichte des Speichermaterials der Außenwand |
|
DRHOOW |
Änderung der Dichte des Speichermaterials mit der Temperatur |
|
LAMOW |
Wärmeleitfähigkeit des Speichermaterials der Außenwand |
|
DLAMOW |
Änderung der Wärmeleitfähigkeit des Speichermaterials mit der Temperatur |
|
CPOW |
Spezifische Wärmekapazität des Speichermaterials der Außenwand |
|
DCPOW |
Änderung der Wärmekapazität des Speichermaterials mit der Temperatur |
|
TREFOW |
Referenztemperatur für die Berechnung der Stoffdaten des Speichermaterials der Außenwand (relevant für FDATAOW=2) |
|
FSPECM |
Schalter für Berücksichtigung der Masse in der Berechnung der fluidseitigen Enthalpiegleichung für FLUID12 und FLUID34 =0: Fluidmasse vernachlässigbar für thermisches Verhalten des Speichers |
|
FTTI |
Schalter für Steuerung der Interpolation der Stoffdaten =1: Ermittelt aus einfachem Mittelwert beim ersten internen Zeitschritt |
|
FTSTEPS |
Schalter für Steuerung der Zeitschrittweite =1: konstant mit Spezwert TISTEP |
|
ISUBMAX |
Maximale Anzahl der internen Iterationsschritte bei der Initialisierung |
|
IERRMAX |
Maximal erlaubter Fehler bei Initialisierungsrechnung |
|
TISTEP |
Vorgabewert für Zeitschrittweite bei FINIT = 1, abhängig von FTSTEPS immer gültig für FINIT = 2, bzw. global gesteuerten Folgedurchlauf (FTSTEPS ist dann ohne Auswirkung!) |
|
NFLOW |
Anzahl der Stützstellen im Rechengitter in X-Richtung (Strömungsrichtung), (max. 100) |
|
NRADBW |
Anzahl der radialen Punkte im Rechengitter in Y-Richtung in der Zwischenwand (bridge wall)), (heiße/kalte Fluidseite, max. 30) |
|
NRADOW |
Anzahl der radialen Punkte im Rechengitter in Y-Richtung in der Außenwand), (max. 30) |
|
FFREQ |
Schalter für Häufigkeit der instationären Berechnungen =1: bei jedem Iterationsschritt |
|
TMIN |
Untergrenze für die Speichertemperatur |
|
TMAX |
Obergrenze für die Speichertemperatur |
|
FSTAMB |
Schalter für Übernahme der Umgebungstemperatur =0: Übernahme konstanter Wert von TAMB |
|
AMB |
Umgebungstemperatur des Wärmetauschers |
|
ISUN |
Index für Solarparameter |
|
TIMETOT0 |
Verstrichene Gesamtzeit zu Beginn des instationären Rechenschrittes (vorletzte Position im Zeitreihendialog) |
|
FRELDIA |
=0: Wärmeaustauscherfläche Brückenwand AWF13 bezieht sich auf den Rohrinnendurchmesser DI =1: Wärmeaustauscherfläche Brückenwand AWF13 bezieht sich auf den Rohraußendurchmesser DA |
|
QN |
Wärmetauscherleistung (nominal) =Q34N |
|
M1N |
primärseitiger Massenstrom (nominal) |
|
M3N |
sekundärseitiger Massenstrom (nominal) |
|
V1N |
spezifisches Volumen für primärseitigen Eintritt (nominal) |
|
V3N |
spezifisches Volumen für sekundärseitigen Eintritt (nominal) |
|
P1N |
Druck für primärseitigen Eintritt (nominal) |
|
P3N |
Druck für sekundärseitigen Eintritt (nominal) |
|
TM34N |
Mittlere Rauchgastemperatur (nominal) TM34N=(T3N+T4N)/2 |
Die blau markierten Parameter sind Referenzgrößen für den Teillastmodus. Die Ist-Teillastwerte beziehen sich in den verwendeten Gleichungen auf diese Größen.
Generell sind alle sichtbaren Eingaben erforderlich. Häufig werden jedoch Standardwerte zur Verfügung gestellt.
Für weitere Informationen über die Farbe der Eingabefelder und ihre Beschreibungen siehe Komponenten bearbeiten\Vorgabewerte
Für weitere Informationen über Auslegung vs. Teillast und Nominalwerte siehe Allgemeines\Nominalwerte übernehmen
|
Q21 |
An das primärseitige FLUD12 übertragene Wärmemenge (bei stationärer Rechnung =QT und Q34, bei instationärer Rechnung die von der Wand aufgenommene Wärmemenge) |
|
QT |
Übertragene Wärmemenge (Achtung bei transienter Rechnung macht dieses Ergebnis keine Aussage mehr, sofern der Speicher noch Wärme aufnimmt oder abgibt!) |
|
Q34 |
Von sekundärseitigen FLUD34 übertragene Wärmemenge (bei stationärer Rechnung =QT und Q12, bei instationärer Rechnung die an die Wände abgegebene Wärmemenge) |
|
KA |
Wärmeübergangskoeffizient mal Fläche aus stationärer WT-Rechnung |
|
DTM |
Mittlere logarithmische Temperaturdifferenz aus stationärer Rechnung |
|
DTLO |
Untere Grädigkeit aus stationärer Rechnung |
|
DTUP |
Obere Grädigkeit aus stationärer Rechnung |
|
REFF |
Berechnete Effektivität (=tatsächlich übertragene Wärme zu theoretischem Maximum bei unendlicher Größe) |
|
X2 |
Dampfgehalt (X) am primärseitigen Austritt |
|
AL12 |
Berechneter Wärmeübergangskoeffizient FLUID12 zum Speicher |
|
AL34 |
Berechneter Wärmeübergangskoeffizient Speicher zu m FLUID34 |
|
DP12 |
Druckabfall primärseitig |
|
DPREF12 |
Nennlast Druckabfall primärseitig |
|
DP34 |
Druckabfall sekundärseitig |
|
DPREF34 |
Nennlast Druckabfall sekundärseitig |
|
VM1 |
Spezifisches Volumen FLUID12 eingangsseitig bei Nennlast |
|
VM3 |
Spezifisches Volumen FLUID34 eingangsseitig bei Nennlast |
|
RADAPT |
Ergebnis ADAPT / EADAPT |
|
M1M1N |
Bezogener Primärmassenstrom |
|
M3M3N |
Bezogener Sekundärmassenstrom |
|
KAKAN |
Bezogener kA-Wert |
|
KAN0 |
dem kA-Wert entsprechendes KAN |
|
TAVBREND |
Kalorisch gemittelte Temperatur der Zwischenwand am Ende des Zeitschrittes |
|
TAVWOEND |
Kalorisch gemittelte Temperatur der Außenwand am Ende des Zeitschrittes |
|
T2AV |
Gemittelte Austrittstemperatur FLUID12 |
|
T4AV |
Gemittelte Austrittstemperatur FLUID34 |
|
TX2BEG |
Temperatur T2 zu Beginn des Zeitschrittes |
|
TX2END |
Temperatur T2 am Ende des Zeitschrittes |
|
TX4BEG |
Temperatur T4 zu Beginn des Zeitschrittes |
|
TX4END |
Temperatur T4 am Ende des Zeitschrittes |
|
QSTO |
In allen Wänden während des Zeitschrittes gespeicherte Energie |
|
QAV12 |
Gemittelter Wärmestrom von der Zwischenwand zum FLUID12 |
|
QAV34 |
Gemittelter Wärmestrom vom FLUID34 zu den Wänden |
|
QAVLOSS |
Gemittelter Wärmestrom von den Wänden an die Umgebung |
|
QENDO |
Wärmestrom am Ende des Zeitschrittes von den Wänden an die Umgebung |
|
RALPHO |
Eingesetzter Wärmeübergangskoeffizient an die Umgebung |
|
THBRW |
Äquivalentdicke der Zwischenwand |
|
THOW |
Äquivalentdicke der Außenwand |
|
REDIA12 |
Primärseitiger Äquivalentdurchmesser FLUID12 |
|
REDIA34 |
Sekundärseitiger Äquivalentdurchmesser FLUID34 |
|
MFL12 |
Masse des FLUIDS12 auf der Primärseite |
|
MFL34 |
Masse des FLUIDS34 auf der Sekundärseite |
|
RELQQ |
Relaxation theoretischer/numerischer Wärmestrom |
|
TIMEINT |
Gesamte Integrationszeit des Zeitschrittes |
|
TIMETOT |
Gesamtzeit der Simulation (Summe der bis zur Auswahl gerechneten Zeitschritte des Zeitreihendialoges) |
|
TIMESUB |
Integrationszeit der Unterschritte (TIMEINT/ISUB) |
|
INSFRAC |
Anteil der instationären Rechenschritte gemäß Vorgabe FFREQ |
|
ISUB |
Anzahl der Unterzeitschritte |
|
TISUBREC |
Empfohlene Zeitschrittweite (aus Fourier- und Biotzahl) |
|
PREC |
Genauigkeitsindikator |
Zur Vorgabe temperaturabhängiger Materialparameter existieren 3 Kennlinien mit jeweils der Temperatur auf der X-Achse:
Die übrigen "Kennlinien" dienen der Koppelung der Zeitschritte untereinander und brauchen i.d.R. vom Anwender nicht beeinflusst werden.
Korrespondierend mit diesen "Kennlinien" gibt es zu jeder Ausgabegröße ein Ergebnisfeld.
Spezifikations-Matrix MXTSTO und Ergebnis-Matrix RXTSTO
Die Matrix MXTSTO ist mit der Ergebnismatrix RXTSTO auf die gleiche Weise verknüpft wie die oben genannten Kennlinien und Ergebnisfelder (bzw. Ergebniskurven). Die Verteilung der Werte im Speicher und den Fluiden wird in beiden Matrizen (Vorgabematrix MXTSTO für den Zeitschritt t-1 und Ergebnismatrix RXTSTO für den Zeitschritt t) abgelegt.
Aufbau der Matrizen siehe Matrizen bei BT 126.
|
|
Für komplexe Wärmetauscherstrukturen können die Speicher- oder Rohrmassen MWF13 (Trennwand zwischen den Fluiden), MWOUT (Außenwand des Speichers), die Wärmeaustauschfläche zwischen den Fluiden AWF13 und die Fläche der Außenwand AWOUT vorgegeben werden. Die Strömungslängen der beiden Fluide werden in LSTO12 und LSTO34 abgelegt.
Aus diesen Parametern wird eine Äquivalentgeometrie für die Wandstärken abgeleitet mit Hilfe der Gleichungen für Rohrgeometrien:
Fall FRELDIA = 0 (AWF13 bezogen auf Rohrinnendurchmesser DI)
DI = DI13 = AWF13 / (LSTO12 * p) und DIWOUT = AWOUT / (LSTO34*p)
|
|
Fall FRELDIA = 1 (AWF13 bezogen auf Rohraußendurchmesser DA)
DA = AWF13 / (LSTO12 * p)
Der zugehörige "Innendurchmesser" DI kann entsprechend angegeben werden :
|
|
Die beiden Wandstärken sind zugänglich mit s = 0.5 * (DA-DI).
Abhängig vom Schalter FVFLUID ist das durchströmte Volumen frei definierbar, oder kann aus den vorhandenen Daten als Volumen eines Rohres berechnet werden.
Für eine bestimmte Temperaturleitfähigkeit
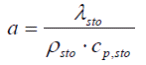 (2.1) (2.1) |
und gegebene Abstände dX und dY zu den Nachbarpunkten wird das Temperaturfeld Θ der Wärmetauscherwandungen berechnet, durch Lösen der Differentialgleichung (DGL) der Wärmeübertragung für jedes diskrete Speicherelement
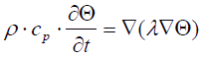 (2.2) (2.2) |
diese kann für die eingeführte Geometrie auf ein eine zweidimensionale Form vereinfacht werden:
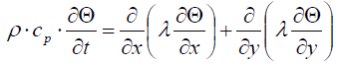 (2.3) (2.3) |
Änderungen des Temperaturfelds finden immer von einem Ausgangszustand aufgrund von Wärmefluss durch das Wandmaterial und seine Isolierungsoberfläche statt (s. 3 weiter unten).
Hinweis: Für bestimmte Berechnungen kann es erforderlich werden, die Außenwand thermisch "verschwinden" zu lassen. Dazu kann sowohl deren Fläche als auch Masse sehr klein gewählt werden mit Diskretisierung in Y-Richtung = 1. Eine Isolierung nach außen kann durch geeignete Wahl von THISO und LAMISO ausgeschaltet werden.
2 Verfahren stehen im Bauteil 126 zur Berechnung der Wandtemperatur zur Verfügung. Analog zum Bauteil 119 wird bei FALGINST=1 die Gleichung (2.3) mit dem Crank-Nicolson-Algorithmus numerisch gelöst. Bei FALGINST=4 wird dagegen das Kombinierte analytische und numerische Modell für die Berechnung der Wandtemperatur verwendet.
Der Wärmefluss zwischen den Speicherwänden und den Fluiden ist abhängig von Position und Zeit und wird für die wärmeübertragenden Wände beschrieben durch die Koppelung von konvektiven (2.4) und konduktiven Termen (2.5):
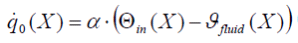 (2.4) (2.4) |
und
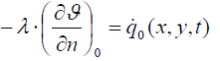 (2.5) (2.5) |
 die Temperatur auf der fluidseitigen Wandfläche bezeichnet.
die Temperatur auf der fluidseitigen Wandfläche bezeichnet. 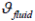 ist die Temperatur des Mediums, und
ist die Temperatur des Mediums, und 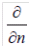 zeigt an, dass die Richtung des Wärmeflusses orthogonal zur Richtung des Medienflusses ist. Der Wärmefluss an der Außenseite der Isolierung wird auf die gleiche Weise berechnet.
zeigt an, dass die Richtung des Wärmeflusses orthogonal zur Richtung des Medienflusses ist. Der Wärmefluss an der Außenseite der Isolierung wird auf die gleiche Weise berechnet.
Der Wärmefluss an den Wänden bewirkt eine Änderung im Temperaturfeld der Arbeitsmedien, was nur durch eine eindimensionale Reihe von Gitterpunkten in Flussrichtung abgebildet wird. Temperaturgradienten, die senkrecht zur Flussrichtung verlaufen, werden wie auch die Strömungsdynamik etc. vernachlässigt, um das Modell einfach zu halten und Rechenzeit zu sparen. Zeitliche Änderungen der Temperaturprofile werden auf der Grundlage von Massen- und Energiebilanz für jedes Volumenelement der Medien berechnet:
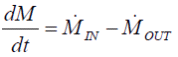 (2.6) (2.6) |
und
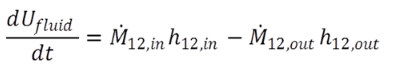 (2.7) (2.7) |
Die differentielle innere Energie eines Fluidelements entspricht 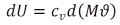 , eingesetzt in Gl 2.7 und umgestellt ergibt sich folgende Teil-Bilanzgleichung, die den Wärmestrom vom Fluid zum Speicher beschreibt:
, eingesetzt in Gl 2.7 und umgestellt ergibt sich folgende Teil-Bilanzgleichung, die den Wärmestrom vom Fluid zum Speicher beschreibt:
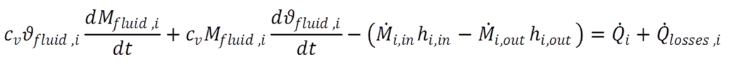 (2.8) (2.8) |
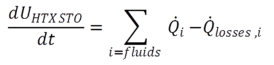 (2.9) (2.9) |
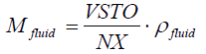 (2.10) (2.10) |
Die Medieneigenschaften werden von EBSILONs Medienbibliothek berechnet.
FSPECM=1: Bei kontinuierlicher Strömung und nicht berücksichtigter Fluidmasse, wird die linke Seite der Gleichung 2.8 zu Null gesetzt. Damit vereinfacht sich die Berechnung zu
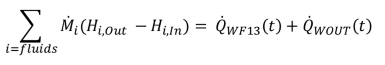 (2.11) (2.11) |
FSPECM=2: Bei kontinuierlicher Strömung oder einem Massenstrom MFluid = 0 findet keine Veränderung der Fluidmasse im inneren des Rohrs statt, jedoch ist die im Fluid gespeicherte Energie nicht vernachlässigbar und wird in der Berechnung beachtet. Gleichung 2.8 erhält folgendes Aussehen:
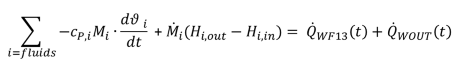 (2.12) (2.12) |
Anwendungsbeispiel: Auskühlen von stehendem Thermofluid in Leitung.
FSPECM=3: Die Fluidmasse im Inneren des Rohrs ist veränderlich, was durch Änderungen der Fluiddichte bei konstantem Volumen in Abhängigkeit von Druck und Temperatur des Fluids am Eintritt bedingt ist, dabei treten unterschiedliche Massenströme am Ein- und Austritt auf.
Anwendungsbeispiel: Ausdampfen eines Behälters nach Druckabfall oder sekundärseitigem Temperatursprung
Die Berechnung der einzelnen Wärmeströme erfolgt nach Gleichung (2.8) und wird ebenfalls mit FSPEM gesteuert. Für den Fall dass die Fluidmasse vernachlässigt werden kann, ergeben sich folgende Zusammenhänge, gültig für die beiden Fluide:
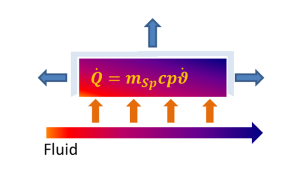 |
Die Speichermasse deren Temperaturänderung einen Wärmestrom (Q0(t)) bewirkt besteht nur aus den Elementen des Speichers. Die Fluide stehen in thermischem Kontakt mit dem Speicher über folgende Gleichung:
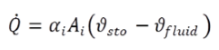 (2.13) (2.13) |
In gleicher Weise ergibt sich die Berechnung des Verlustwärmestroms an die Umgebung (blaue Pfeile), angezeigt mit den Werten QAVLOSS und QENDO. Der transiente Speicherterm wird, integral betrachtet gebildet durch:
 (2.14) (2.14) |
Die Bilanzierung aller Wärmeströme (entsprechend Gl.(11)) liefert mit einer weiteren Integration über den Zeitschritt die gespeicherte Wärmemenge, abgelegt in der Ergebnisvariable QSTO:
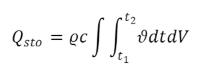 (2.15) (2.15) |
Dividiert man diesen Wert durch die Zeitschrittweite Dt, so ergibt sich die im Mittel ausgetauschte Wärmemenge QAV12 (Zwischenwand und FLUID12), bzw. QAV34 (Zwischenwand, Außenwand und FLUID34).
Hinweis: Je nachdem wie groß die Temperaturgradienten über den Zeitschritt ausfallen und wie die Zeitschrittweite gewählt wurde, kann die Bilanz nicht ganz geschlossen werden! Bei größeren Diskrepanzen empfiehlt sich die Wahl kleinerer Zeitintervalle, bzw. eine Verfeinerung der Berechnung mit FTSTEPS.
Wird die Fluidmasse (FSPEM = 2,3) bei den Berechnungen mit berücksichtigt, nimmt die Bilanzierung eine veränderte Form an:
 |
Die linke Seite von Gl. 2.8 ist nicht mehr 0, die Masse des Fluids wird zusätzlich Bestandteil dieser Gleichung. Fluid und Wandungen bilden nun das speichernde System.
Der Schalter FINST steuert das instationäre Verhalten des Bauteils
FINST=0: Die Zeitschrittweite der einzelnen Rechenschritte ist durch die Zeitreihe vorgegeben. Die Berechnung erfolgt ausschließlich mithilfe des Rechenbefehls im Zeitreihenmenü. Alle instationären Gleichungsterme, die ein Speicherverhalten beinhalten werden berechnet.
FINST=1: Die Berechnung ist stationär, das Bauteil wird wie ein stationärer Wärmeübertrager berechnet. Falls den Wärmeübergang betreffende Spezifikationswerte geändert werden, führen diese lediglich zu einer neuen stationären Lösung für das Bauteil. Sämtliche zeitabhängigen Speicherterme werden nicht berücksichtigt!
Initialisierung der Simulation mit dem Schalter FINIT
FINIT=1: Entsprechend den Spezifikationswerten wird der Wärmetauscher mit der stationären Lösung initialisiert. Eine erste transiente Rechnung wird ausgeführt mit dem Ziel den Zustand der Langzeitasymptote zu erreichen. Die Matrizen, die die Temperaturverteilungen beinhalten, erhalten dieses Ergebnis als Startwert für die transiente Rechnung.
Je nachdem, wie das Problem aufgesetzt ist, kann es zu sehr langen Rechenzeiten bei der Initialisierung kommen. Um dies zu steuern und optimieren zu können, kann der Anwender über folgende Vorgabewerte Einfluss auf die Simulation nehmen:
FTSTEPS, ISUBMAX, IERRMAX, TISTEP
Wie erwähnt, ist die Initialisierung der Simulation eine Berechnung der Lösung für t->inf. In der Praxis muss hier in Bezug auf Genauigkeit und Rechenzeit stets ein Kompromiss gefunden werden. Damit im Zeitreihendialog nicht unnötig viele Zeilen mit den Zeitschritten dieser Berechnungen auftauchen, werden diese Schritte modellintern durchgeführt und nur deren Endergebnis nach Erreichen der Abbruchkriterien angezeigt. Mit ISUBMAX kann die maximale Anzahl dieser Rechenschritte begrenzt werden (i.d.R. sollten nicht mehr als 1000 erforderlich sein.) und zusätzlich kann der numerische Fehler, dargestellt in der Ergebnisvariable PREC (Vergleich der von den Fluiden aufgenommenen, bzw. abgegebenen Wärmeströme mit denjenigen durch die Speicherwände -> konvergiert für die stationäre Lösung, beinhaltet aber stets einen numerischen "Restfehler"!) Über IERRMAX kann hierfür eine Grenze festgelegt werden, bei deren Unterschreiten (i.d.R. 10-6 ausreichend) die Rechnung abgebrochen wird.
Mit FTSTEPS und TISTEP kann das Konvergenzverhalten gesteuert werden. Zum einen kann die Zeitschrittweite über die Gitterkennzahlen bestimmt werden, zum anderen erlaubt eine Vorgabe des Zeitschrittes eine individuelle Anpassung. Bei der Wahl der Schrittweiten ist zu beachten, dass zu große Werte zu oszillierenden oder gar divergierenden Lösungen führen können, an dieser Stelle sei auf die Warnungen, bzw. Fehleranzeigen verwiesen, TSUBREC liefert hier einen zusätzlichen Anhaltspunkt.
Der Vorgabewert TISTEP wird immer auch in der eigentlichen instationären Rechnung verwendet. Ist dieser größer als die von Zeitreihendialog vorgegebene Schrittweite, so wird innerhalb der Komponente nur dieser eine Zeitschritt gerechnet. Ist TISTEP kleiner, führt dies ebenso, wie bei der Initialisierung zur Berechnung von modellinternen (Unter-)Zeitschritten (Ergebniswert ISUB), deren Zwischenergebnisse nicht angezeigt werden.
Hinweis: Mit der Angabe der Wärmeübergangskoeffizienten AL12N und AL34N sowie Lambda der Rohrwandung (Bridgewall) zwischen den Fluiden wird der k-Wert für den Wärmetauscher gemäß Gl 3.1 festgelegt. Di berechnet sich aus der Fläche AWF13/(LSTO12*p), der Außendurchmesser wird erhalten aus:
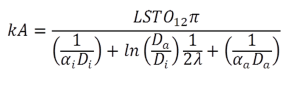 (3.1) (3.1) |
Die zusätzliche Spezifikation der Wärmetauscherfläche (AWF13), legt somit auch kA explizit fest. Mit den vorgegebenen Alpha-Werten weisen somit die stationäre und instationäre Simulation identischen Input auf. Designfälle, die einen kA-Wert berechnen sind hier nicht sinnvoll und im Gegensatz zu den rein stationären Wärmetauschermodellen nicht wählbar!
FINIT=2: Die Berechnung erfolgt entsprechend den Vorgaben des Zeitreihendialoges. Die Ergebnisse des vorangegangenen Zeitschrittes bilden die Eingabe für den darauf folgenden Schritt.
 |
Form 1 |
 |
Form 2 |
 |
Form 3 |
 |
Form 4 |
 |
Form 5 |
 |
Form 6 |
 |
Form 7 |
 |
Form 8 |
 |
Form 9 |
 |
Form 10 |
 |
Form 11 |
 |
Form 12 |
 |
Form 13 |
 |
Form 14 |
Klicken Sie hier >> Bauteil 126 Demo 1 << um ein Beispiel (Vorwärmer mit Kennlinien für Materialparameter) zu laden.
Klicken Sie hier >> Bauteil 126 Demo 2 << um ein Beispiel 2 (Allgemeiner WT mit Verlusten an die Umgebung) zu laden.
Klicken Sie hier >> Bauteil 126 Demo 3 << um ein Beispiel 3 (Überhitzer mit Ausdampfen) zu laden.