

|
Leitungsanschlüsse |
|
|
|
1 |
Einströmung |
|
|
2 |
Ausströmung |
|
|
3 |
Wärmeübertragung vom Fluid zum Speichermedium |
|
Allgemeines Vorgabewerte Verwendete Physik / Gleichungen Kennlinien und Matrizen Ergebniswerte Bauteilform Beispiel
Dieses Bauteil stellt einen Einstieg in die Abbildung instationärer Prozesse in Ebsilon dar. Obwohl Ebsilon vom Grundsatz her auf stationäre Lösungen beschränkt ist, weil die Bauteilgleichungen keine Zeitabhängigkeit enthalten und Ebsilon deshalb ein stationäres Gleichungssystem löst, ermöglicht dieses Bauteil durch Hinzunahme entsprechender Quell- und Senkenterme die Abbildung instationärer Vorgänge wie beispielsweise
Das Bauteil indirekter Speicher berechnet den instationären Wärmeaustausch des Materials mit dem es durchströmenden bzw. umströmenden Fluid. Dazu wird die durchströmte Struktur durch ein Rohrmodell gleicher Masse, Wärmetauscherfläche und Werkstoffkennwerte abgebildet. Der Einfluss der Strömungsart und der Geometrie der realen Struktur auf den Wärmeübergang wird durch den Wärmeübergangskoeffizienten an der Wärmeübergangsfläche im inneren des Rohrs berücksichtigt. Die Modellierung als Rohr hat den Vorteil, dass eine Vielzahl von technischen Anwendungen sich auf die Theorie des Wärmeübergangs in Rohren übertragen lässt. Ein weiterer Vorteil der Rohrgeometrie sind die kreissymmetrische Temperaturverteilung und Wärmeübertragung, so dass die Berechnung des Temperaturfelds auf einen Querschnitt längs der Strömungsrichtung reduziert wird. Die instationären Berechnungen fügen sich dabei als Wärmequellen- und Wärmesenkenterme in die klassischen stationären Iterationen ein. Im Hinblick auf eine Rohrleitung erweitert sich die Energiebilanz um die transienten Terme wie folgt:
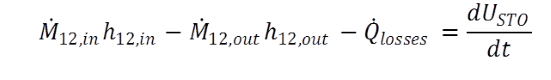 |
Von einem Ausgangszustand des Temperaturfelds aus berechnet das BT119 die Veränderung des Temperaturfelds des Rohrs infolge einer Veränderung der Rahmenbedingungen innerhalb eines definierten Zeitraums. Die Rahmenbedingungen sind durch die Spez-Werte des Bauteils sowie die Zustandsgrößen des Fluid am Bauteileingang definiert. Das Bauteil muss in Kombination mit der Zeitreihenrechnung verwendet werden, in welcher der Berechnungszeitraum definiert wird und mit dem die Rahmenbedingungen zu definierten Zeitpunkten verändert werden können. Während eines Berechnungsschritts der Zeitreihenrechnung bleiben die Spezifikationswerte und Zustandsgrößen der Schaltung konstant
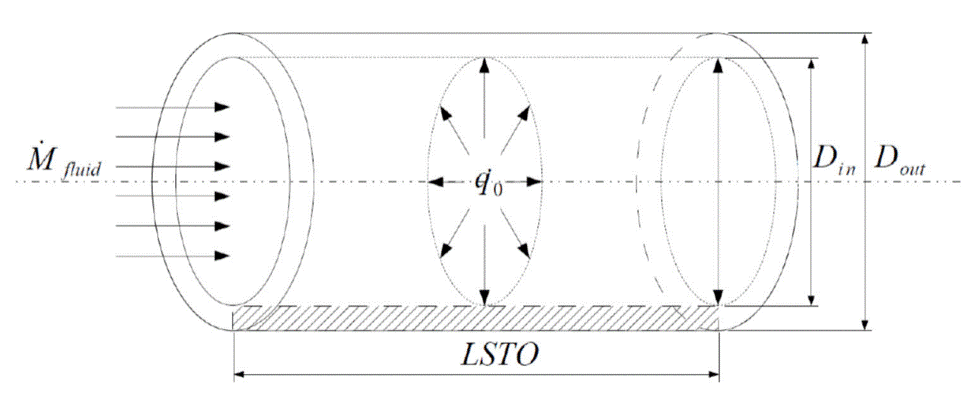
Abbildung 1: Geometrie des Rohrs
Dazu wurde der Schalter FDP eingeführt. Bei
Die Geometrie basierte Druckverlustberechnung ist nur dann sinnvoll, wenn das Bauteil 119 ein echtes Rohr modelliert. Zu Berechnung des Druckverlusts wird in diesem Fall außer dem Volumenstrom des Mediums der innere Durchmesser DIAI, die Rohrlänge LSTO sowie die Wandrauigkeit KS verwendet.
|
FMODE |
Vorgabe des Berechnungsmodus |
|
FINIT
|
Vorgabe des Anfangszustands =0: GLOBAL, die Steuerung erfolgt über die globale Variable "Instationärer Modus" unter Modell-Einstellungen: =1: erster Durchlauf, das Temperaturfeld wird gemäß FSTART initiiert |
|
FINST
|
Schalter zur Bestimmung des Instationaritätsmodus 0: Instationäre Lösung nach Zeitreihen- Dialog |
|
FALGINST |
Schalter für instationären Berechnungsmodus =1: Crank-Nicolson-Algorithmus |
|
FSTO |
Festlegung der Definition der Rohrgeometrie, die für die Masse sowie die Wärmetauscherfläche ausschlaggebend ist: =0: Vorgabe der Strömungslänge, der Wärmetauscherfläche und der Speichermasse |
|
LSTO |
Strömungslänge des Speichers |
|
DIAI |
Innendurchmesser des Rohrspeichers |
|
THSTO |
Wandstärke des Rohrspeichers |
|
ASTO |
Austauschfläche des Rohrspeichers |
|
MSTO |
Masse des Rohrspeichers |
|
FVFLUID |
Festlegung der Fluidvolumens, das die Fluidmasse bei gegebener Fluiddichte definiert =0: Fluidvolumen durch VFLUID definiert |
|
VFLUID |
Strömungsvolumen des Fluids |
| FMAT |
Materialkennzahl, siehe Stahlsorten |
|
FDATA
|
Vorgabe der Stoffwerte des Speichermaterials =1: konstant gemäß RHO, LAM, CP |
|
RHO |
Dichte des Speichermaterials bei TREF, oder konstant und unabhängig von TREF bei FDATA = 1 |
|
DRHO |
Dichteänderung pro Kelvin definiert die Steigung der linearen Funktion für FDATA=2 |
|
LAM |
Wärmeleitfähigkeit des Speichermaterials bei TREF, oder konstant und unabhängig von TREF bei FDATA = 1 |
|
DLAM |
Wärmeleitfähigkeitsänderung pro Kelvin definiert die Steigung der linearen Funktion für FDATA=2 |
|
CP |
Spezifische Wärmekapazität des Speichermaterials bei TREF, oder konstant und unabhängig von TREF bei FDATA = 1 |
|
DCP |
Äderung der spezifischen Wärmekapazität pro Kelvin definiert die Steigung der linearen Funktion für FDATA=2 |
| ERHO | Funktion für die Dichte des Materials |
| ELAM | Funktion für die Wärmeleitfähigkeit des Materials |
| ECP | Funktion für die Wärmekapazität des Materials |
|
TREF |
Referenztemperatur für FDATA=2 |
|
THISO |
Dicke der Isolierung |
|
LAMISO |
Wärmeleitfähigkeit der Isolierung |
|
TAUADJ |
Korrekturfaktor für die Zeitkonstante der Rohrwand (reduziertes physikalisches Modell) |
|
LAMADJ |
Multiplikator zu 1/LAMBDA - Widerstand durch die Wärmeleitfähigkeit der Rohrwand (reduziertes physikalisches Modell)
Setzen LAMADJ=0 ist äquivalent zum Vernachlässigen des Widerstands durch die Wärmeleitfähigkeit der Rohrwand: entspricht entweder einer unendlich dünnen Rohrwand oder einem unendlich hohen Lambda-Wert Setzen LAMADJ=1 is äquivalent zur Berechnung des Widerstands durch die Wärmeleitfähigkeit der Rohrwand mit den Originalwerten vom LAMBDA und von der Rohrwandstärke LAMADJ<1 führt zur Verkleinerung des Widerstands durch die Wärmeleitfähigkeit der Rohrwand LAMADJ>1 führt zur Vergrößerung des Widerstands durch die Wärmeleitfähigkeit der Rohrwand |
|
FSPECM |
Schalter zur Berücksichtigung der Fluidmasse =1: Fluidmasse vernachlässigbar, |
|
FTTI |
Schalter zur Interpolation der temperaturabhängigen Kenngrößen für die Stoffwerte CP, LAM, RHO =0: Temperatur am Ende des Zeitschrittes |
|
FTSTEPS |
Art der Vorgabe des Zeitschritts der zeitlichen Diskretisierung (Unterzeitschritt) =1: gemäß TISTEP |
|
ISUBMAX |
Maximale Anzahl der internen Iterationsschritte bei der Initialisierung |
|
IERRMAX |
Maximal erlaubter Fehler bei Initialisierungsrechnung |
|
TISTEP |
Wert des Unterzeitschritts bei FINIT = 1, abhängig von FTSTEPS, für FTSTEPS=1 -> Legt TIMESUB fest und damit ISUB immer gültig für FINIT = 2, bzw. global gesteuerten Folgedurchlauf (FTSTEPS ist dann ohne Auswirkung) |
| FNUMSC |
Numerisches Schema =0: Upwind Verfahren |
|
NFLOW |
Anzahl der Gitterpunkte des numerischen Gitters (räumliche Diskretisierung des Temperaturfelds) in Strömungsrichtung. Bei FSPECM=4 gilt NX=1. (max. 300) |
|
NRAD |
Anzahl der Gitterpunkte des numerischen Gitters (räumliche Diskretisierung des Temperaturfelds) in radialer Richtung (max. 30) |
|
TIMESING |
Dauer des Zeitschritts der Einzelrechnung bei FINST=2 |
|
FFREQ
|
Schalter für Häufigkeit instationärer Berechnungen: 1: In jedem Iterationsschritt |
|
FSTART
|
Definition der Initiierung des Temperaturfelds =1: jeder Gitterpunkt des Temperaturfelds entspricht TSTART |
|
TSTART |
Startemperatur des Temperaturfelds für FSTART=1 |
|
TMIN |
Untergrenze für Speichertemperatur |
|
TMAX |
Obergrenze für Speichertemperatur |
|
FSTAMB
|
Vorgabe der Umgebungstemperatur |
|
TAMB |
Umgebungstemperatur |
|
ISUN |
Index der übergeordneten Berechnung aus der die Umgebungstemperatur übernommen wird (z.B. BT 117) |
|
FALPHI
|
Vorgabe des Wärmeübergangskoeffizienten an der Rohrinnenseite =0: konstant gemäß ALPHI |
|
ALPHI |
Konstanter Wärmeübergangskoeffizient vom Fluid an die Rohrinnenseite für den Auslegungsfall bei FALPHI=0; |
|
EALPHI |
Parameterabhängige Funktion des Wärmeübergangskoeffizienten an der Rohrinnenseite - In der Expression können die Werte der Fluidtemperatur T_FLUID und der Wandtemperatur T_WALL als Argumente benutzt werden (z. B. Berechnung des Strahlungswärmeübergangs) |
|
FALPHO |
Vorgabe des Wärmeübergangskoeffizienten an der Rohraußenseite =0: konstant gemäß ALPHO |
|
ALPHO |
Konstanter Wärmeübergangskoeffizient an der Rohraußenseite für FALPHO=0 |
|
EALPHO |
Parameterabhängige Funktion des Wärmeübergangskoeffizienten an der Rohraußenseite |
|
EX12 |
Massenstromexponent des inneren Wärmeübergangskoeffizienten |
| FHC |
Berücksichtigung der Wärmeleitung im Fluid =0: vernachlässigt |
| CLMFL | Fluid-Wärmeleitungs-Korrekturfaktor für Lambda (z.B. wegen freier Konvektion) |
| FDP |
Methode für Druckverlustberechnung =0: Vorgabewert DP12N benutzen |
|
FVOL |
Schalter für die Berücksichtigung der Abhängigkeit des Druckverlusts =0: nur Massenstrom-abhängig DP/DPN = (M1/M1N)**2 |
| FDPNUM |
Druckverlusthandhabung in der numerischen Lösung =0: Benutzen des mittleren Fluiddruckes zwischen Ein- und Austritt |
| FDPBASE |
Druckverlustberechnung bei der Off-Design-Rechnung =0: als Bezugsgröße wird der Mittelwert des spezifischen Volumens zwischen Ein- und Austritt verwendet |
|
DP12N |
Druckabfall (nominal) |
| KS | Äquivalente Sandrauhigkeit |
|
TAVSTART |
Startwert für mittlere Mediumtemperatur |
|
HAVSTART |
Startwert für mittlere Fluidenthalpie |
|
PAVSTART |
Startwert für mittleren Fluiddruck / für Druck in Fall der Druckberechnung |
|
FDIR |
Schalter für die Behandlung der Strömungsrichtung des Fluids Umkehrung der Fließrichtung im durchströmten Rohr wird durch ein vertikales Spiegeln des numerischen Gitters erreicht (z.B. für die Realisierung von Rauchgas-LUVOs). Orientierung der Anschlüsse nach Ein- und Ausgang bleibt unverändert. =0: Normal, keine Änderung der Fließrichtung =1: Umgekehrt, vertikale Spiegelung (Achtung: Die Spiegelung findet jedes Mal bei dieser Schalterstellung statt!) |
|
TIMETOT0 |
Gesamtzeit zu Beginn der Berechnung (Summe vorangegangene Zeitschritte) |
|
M1N |
Massenstrom (nominal) |
|
V1N |
Spezifisches Volumen am Eintritt (nominal) |
|
V12N |
Spezifisches Volumen (Mittelwert zwischen Eintritt und Austritt) (nominal) - siehe auch FDPBASE |
|
TM12N |
Mittlere Temperatur zur Berechnung der Alphazahl (nominal) |
Die blau markierten Parameter sind Referenzgrößen für den Teillastmodus. Die Ist-Teillastwerte beziehen sich in den verwendeten Gleichungen auf diese Größen.
Generell sind alle sichtbaren Eingaben erforderlich. Häufig werden jedoch Standardwerte zur Verfügung gestellt.
Für weitere Informationen über die Farbe der Eingabefelder und ihre Beschreibungen siehe Komponenten bearbeiten\Vorgabewerte
Für weitere Informationen über Auslegung vs. Teillast und Nominalwerte siehe Allgemeines\Nominalwerte übernehmen
|
TAVBEG |
Kalorisch gemittelte Speichertemperatur zu Beginn des Zeitschrittes |
|
TAVEND |
Kalorisch gemittelte Speichertemperatur am Ende des Zeitschrittes |
|
T2BEG |
Austrittstemperatur des Fluids zu Beginn des Zeitschrittes |
|
T2END |
Austrittstemperatur des Fluids am Ende des Zeitschrittes |
|
RTAMB |
Umgebungstemperatur |
|
QSTO |
Während des Zeitschrittes gespeicherte Wärmemenge je nach Modus FSPECM =1: nur die Rohrmasse ist thermischer Speicher |
|
QAV |
Mittlerer Wärmestrom durch den Speicher (QSTO/TIMEINT) |
|
QEND |
Wärmestrom durch den Speicher am Ende des Zeitschrittes |
|
QAVI |
Mittlerer Wärmestrom vom Fluid zum Speicher |
|
QENDI |
Wärmestrom vom Fluid zum Speicher am Ende des Zeitschrittes |
|
QAVO |
Mittlerer Wärmestrom vom Speicher an die Umgebung |
|
QENDO |
Wärmestrom vom Speicher an die Umgebung am Ende des Zeitschrittes |
|
RALPHI |
Berechneter Wärmeübergangskoeffizient Fluid-Speicher |
|
RALPHO |
Berechneter Wärmeübergangskoeffizient Speicher-Umgebung |
|
RASTO |
Für Wärmeübergang relevante Fläche |
|
RMSTO |
Masse des Speichers (nur Speichermaterial ohne Fluid) |
|
RDIAI |
Rohrinnendurchmesser |
|
RTHSTO |
Wandstärke Speicherrohr |
|
RDIAO |
Rohraußendurchmesser |
|
RVFLUID |
Gesamtes Fluidvolumen im Speicher |
|
MFLUID |
Gesamte Fluidmasse im Speicher |
|
RHOFLAV |
Mittlere Fluiddichte |
|
PFLAV |
Mittlerer Fluiddruck |
|
HFLAV |
Mittlere Fluidenthalpie |
|
TFLAV |
Mittlere Fluidtemperatur |
|
BIOT |
Biotzahl |
|
FOUR |
Fourierzahl |
|
TIMEINT |
Integrationszeit des aktuellen Zeitschrittes (Übernahme aus dem Zeitreihendialog) |
|
TIMETOT |
Gesamtzeit am Ende der Berechnung (Summe aller Zeitschritte) |
|
TIMESUB |
Zeitintervall für die Sub-Zeitschritte (gemäß Vorgabe TISTEP und FTSTEPS) |
|
INSFRAC |
Anzahl der instationären Rechenschritte (abhängig vom Spez-Wert FFREQ) |
|
ISUB |
Anzahl der Sub-Zeitschritte (Es gilt: ISUB * TIMESUB = TIMEINT) |
|
TISUBREC |
Empfohlene Zeitsschrittweite, berechnet aus Kennzahlen (Fourierzahl, Temperaturleitfähigkeit und Gitterkonstante) |
|
PREC |
Genauigkeitsindikator |
FSTO=0: durch LSTO, ASTO und MSTO
Für komplexe Strukturen kann die Speicher- oder Rohrmasse MSTO, die Wärmeaustauschfläche ASTO und die Länge der Struktur LSTO vorgegeben werden. Aus diesen Parametern wird die Rohrgeometrie abgeleitet mit Hilfe der Gleichung für die Wärmeaustauschoberfläche und die Masse der Rohrs:
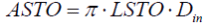 |
(1) |
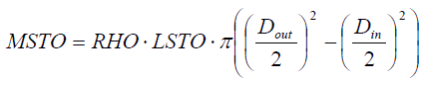 |
(2) |
wobei Dout und Din der innere und äußere Durchmesser des Rohrs sind und RHO die Materialdichte des Rohrs.
Die Rohrgeometrie wird dann definiert als:
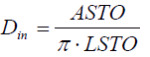 |
(3) |
 |
(4) |
Das mit Medium gefüllte Volumen kann durch die Geometrie des Rohrs definiert werden als:
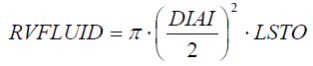 |
(5) |
oder durch einen spezifischen Wert VSTO, was wiederum nützlich ist im Fall einer komplexen Struktur, deren inneres Volumen von einem Rohrmodell abweicht. Daher ist das Speicherbauteil ein flexibler Ansatz für ein sehr großes Feld von Modellierungsanwendungen.
FSTO=1: durch LSTO, DIAI und THSTO
Alternativ kann die Geometrie des Speichers durch die Parameter als ein Rohr definiert werden:
LSTO: Rohrlänge
DIAI: Innerer Durchmesser des Rohrs
THSTO: Rohrwanddicke
Eine Off-Design-Druckverlustberechnung, die sich auf das spezifische Volumen am Eintritt des Bauteils bezieht, kann zu höheren Ungenauigkeiten führen, wenn die Temperaturänderung zwischen Ein- und Austritt hoch ist und das strömende Medium kompressibel / gasförmig ist.
Darum gibt es den Schalter FDPBASE, bei dem auch der Mittelwert des spezifischen Volumens zwischen Ein- und Austritt verwendet werden kann und als Bezugsgröße den Nominalwert V12N (das mittlere spezifische Volumen zwischen Ein- und Austritt).
Für eine bestimmte Temperaturleitfähigkeit:
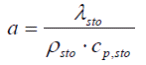 |
(6) |
und gegebene Abständen dX und dY zu den Nachbarpunkten wird das Temperaturfeld Θ des Rohrs berechnet, durch Lösen der Differentialgleichung (DGL) der Wärmeübertragung für jedes Speicherelement:
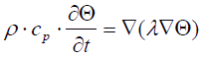 |
(7) |
was auf seine zweidimensionale Form vereinfacht werden kann:
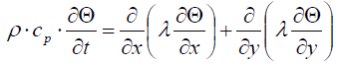 |
(8) |
Änderungen des Temperaturfelds finden immer von einem Ausgangszustand aufgrund von Wärmefluss durch das Rohrmaterial und seine Isolierungsoberfläche statt (s. 3 weiter unten).
Im Fall FALGINST=1 (2D-Gitter Crank-Nicolson-Algorithmus) wird de Gleichung (8) numerisch diskretisiert und gelöst. Die Anzahl der Gitterpunkte in X-Richtung (hier die Strömungsrichtung des Fluids) kann vom Benutzer in Vorgabewert NFLOW verändert werden. Die Anzahl der Gitterpunkte in Y-Richtung (hier die Rohrwandnormale Richtung) kann vom Benutzer in Vorgabewert NRAD verändert werden. Als Ergebnis entsteht eine 2-dimensionale Temperaturverteilung in Speicherwand, die in Matrix MXTSTO, RXTSTO (s. unten) gesichtet werden kann.
Im Fall FALGINST=4 (Modell verwendet kombinierte analytische und numerische Methoden) wird dagegen in wandnormaler Y-Richtung mit nur 1 Gitterpunkt (Zelle) diskretisiert. Für jede Wandzelle wird eine mittlere Wandtemperatur gesucht. Die Wärmeleitung in der Wand in der Strömungsrichtung wird hier vernachlässigt.
Damit lässt sich die Speicherwandtemperatur nach dem Zeitintervall Dt wie folgt berechnen
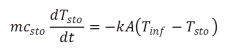 |
(8.1) |
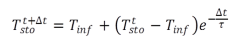 |
(8.2) |
Da innerhalb eines Diskretisierungselementes keine Temperaturgradienten auftreten, kann dieser Ansatz direkt integriert werden und man erhält die in Gleichung (8.2) dargestellte Form der Lösung für die Speichertemperatur in Abhängigkeit der Zeitschrittweite. Die beiden Temperaturen mit dem Index „sto“ bezeichnen den Zustand des Speichers vor und nach dem Zeitintervall Dt, Tinf bezeichnet hier als treibende Kraft die stationäre Endtemperatur des Speichers und t ist die Speicherzeitkonstante mc/kA.
Der Wärmefluss zwischen Speichermaterial und Fluid ist abhängig von Position und Zeit und wird für die Innenseite des Rohrs beschrieben durch:
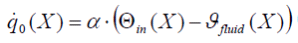 |
(9a) |
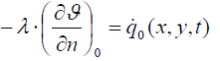 |
(9b) |
wobei Qin die Temperatur auf der Innenoberfläche des Rohrs ist, Jfluid die Temperatur des Mediums ist, und 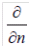 anzeigt, dass die Richtung des Wärmeflusses orthogonal zur Richtung des Medienflusses ist. Der Wärmefluss an der Außenseite der Isolierung wird auf die gleiche Weise berechnet.
anzeigt, dass die Richtung des Wärmeflusses orthogonal zur Richtung des Medienflusses ist. Der Wärmefluss an der Außenseite der Isolierung wird auf die gleiche Weise berechnet.
Der Wärmefluss an der Innenseite bewirkt eine Änderung im Temperaturfeld des Arbeitsmediums, was nur durch eine eindimensionale Reihe von Gitterpunkten in Flussrichtung abgebildet wird. Temperaturgradienten, die senkrecht zur Flussrichtung verlaufen, werden wie auch die Strömungsdynamik etc. vernachlässigt, um das Modell einfach zu halten und Rechenzeit zu sparen. Zeitliche Änderungen des Temperaturprofils werden auf der Grundlage von Massen- und Energiebilanz für jedes Volumenelement des Mediums berechnet:
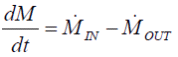 |
(10a) |
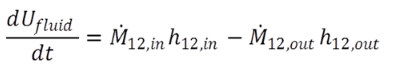 |
(10b) |
Die differentielle Änderung der innere Energie eines Fluidelements entspricht 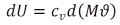 , eingesetzt in die linke Seite von (10b) und erweitert mit der inneren Energie des Rohr-Speichers ergibt sich:
, eingesetzt in die linke Seite von (10b) und erweitert mit der inneren Energie des Rohr-Speichers ergibt sich:
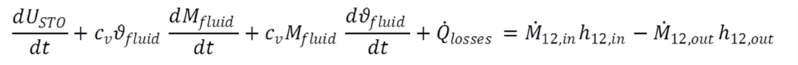 |
(11) |
Die ersten drei Terme der linken Gleichungsseite zeigen die in den Medien enthaltene innere Energie, die rechte Seite bilanziert den resultierenden Wärmestrom aufgrund von Massen- und Enthalpiedifferenz im Fluid. Die Ausgangsmasse eines Medienelements wird definiert durch:
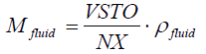 |
(12) |
Die Medieneigenschaften werden mit EBSILONs Stoffwertbibliothek berechnet.
Vor Release 17 war das numerische Schema für die Berechnung der Fluidtemperaturen vom Schalter FSPECM abhängig. Für FSPECM=1 (Fluidmasse vernachlässigt) wurde immer das Schema CDS (Zentraldifferenzen) verwendet. Für FSPECM>1 (Fluidmasse berücksichtigt) wurde das Upwind-Schema verwendet.
Das CDS-Schema hat eine höhere Genauigkeit gegenüber Upwind-Schema. Das Upwind-Schema ist dagegen stabiler für die Innere Konvergenz des Bauteils.
Ab Release 17 gibt es den Schalter FNUMSC. Damit hat der Benutzer die Möglichkeit, unabhängig vom FSPECM-Wert das numerische Schema zu wählen. FNUMSC=0 entspricht dem Upwind-Schema, FNUMSC=1 entspricht dem CDS-Schema.
Sollte in der inneren Iteration aufgrund von erkannten Konvergenz-Problemen vom CDS auf Upwind umgeschaltet werden, wird der Benutzer am Ende der Simulation davon gewarnt.
In den Schaltungen, die mit früheren EBSILON-Versionen als Release 17 gespeichert wurden, wird beim Laden der Wert von FNUMSC-Schalter in Abhängigkeit vom Schalter FSPECM gesetzt, um die alten Ergebnisse zu reproduzieren. Jedoch funktioniert dieses automatische Setzen des Schalters nicht, wenn FSPECM keinen einfachen gültigen numerischen Wert hat, sondern z.B. ein Verweis (Kernelexpression) auf weitere Bauteile enthält. In einem solchen Fall möge der Benutzer selbst den Schalter FNUMSC so setzen, dass die alten Ergebnisse reproduziert werden.
FSPECM=1: Bei kontinuierlicher Strömung und im Vergleich zur Rohrmasse vernachlässigbarer Fluidmasse, wird die linke Seite der Gleichung 10b zu Null gesetzt. Damit vereinfacht sich die Berechnung zu
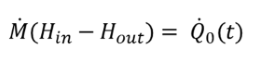 |
(13) |
FSPECM=2: Bei kontinuierlicher Strömung oder einem Massenstrom MFluid = 0 findet keine Veränderung der Fluidmasse im inneren des Rohrs statt, jedoch ist die im Fluid gespeicherte Energie nicht vernachlässigbar und wird in der Berechnung beachtet. Anwendungsbeispiel: Auskühlen von stehendem Thermofluid in Leitung.
FSPECM=3: Die Fluidmasse im Inneren des Rohrs ist veränderlich, was durch Änderungen der Fluiddichte bei konstantem Volumen in Abhängigkeit von Druck und Temperatur des Fluids über die Rohrlänge hinweg bedingt ist, dabei können unterschiedliche Massenströme am Ein- und Austritt auftreten. Um den Zustand des Fluids am Beginn der Zeitreihenrechnung zu definieren, stehen die Spez-Werte TAVSTART, HAVSTART, PAVSTART zur Verfügung. Anwendungsbeispiel:
Ausdampfen eines Behälters nach Druckabfall.
FSPECM=4: Vorgegeben wird der Eingangs- und Austrittsmassenstrom woraufhin sich die Zustandsgrößen des Fluids sowie die im Speicher befindliche Fluidmasse verändern. Das numerische Gitter beschränkt sich auf einen einzelnen Punkt in Strömungsrichtung, abweichende Angaben von NX werden ignoriert. Der Anfangszustand des Fluids am Beginn der Zeitreihenrechnung wird definiert mit Hilfe der Spez-Werte TAVSTART, HAVSTART, PAVSTART. Damit ist auch die anfängliche Fluidmasse im Speicher festgelegt durch m = r(p,H) V.
Die Berechnung der einzelnen Wärmeströme erfolgt nach Gleichung (11) und wird ebenfalls mit FSPEM gesteuert. Für den Fall dass die Fluidmasse vernachlässigt werden kann, ergeben sich folgende Zusammenhänge:
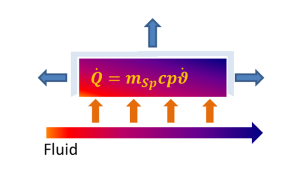 |
Die Speichermasse deren Temperaturänderung einen Wärmestrom Q0(t) bewirkt besteht nur aus den Elementen des Rohres. Das Fluid steht in thermischem Kontakt mit dem Speicher über folgende Gleichung:
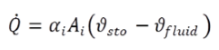 |
(14) |
In gleicher Weise ergibt sich die Berechnung des Verlustwärmestroms an die Umgebung (blaue Pfeile), angezeigt mit den Werten QAVO und QENDO. Der transiente Speicherterm wird integral betrachtet gebildet durch:
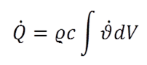 |
(15) |
Die Bilanzierung aller Wärmeströme (entsprechend Gl.(11)) liefert mit einer weiteren Integration über den Zeitschritt die gespeicherte Wärmemenge, abgelegt in der Ergebnisvariable QSTO:
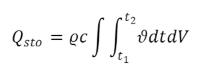 |
(16) |
Dividiert man diesen Wert durch die Zeitschrittweite Dt, so ergibt sich die im Mittel ausgetauschte Wärmemenge QAV. Da sich dieser Wärmestrom mit der Zeit ebenfalls ändert, wird zusätzlich der Wert am Ende des Zeitschrittes ausgegeben und in der Variable QEND abgelegt. Zum Schließen der Energiebilanz findet die vom Fluid abgegebene, bzw. aufgenommene Enthalpie Eingang in die Berechnungen. QAVI zeigt den über das Zeitintervall gemittelten Wärmestrom, während QENDI den Wert am Ende des Zeitschrittes beinhaltet. Dieser wird auf Anschluss 3 ausgegeben. Die Bilanz zeigt folgende Zusammenhänge:
Hinweis: Je nachdem wie groß die Temperaturgradienten über den Zeitschritt ausfallen und wie die Zeitschrittweite gewählt wurde, kann die Bilanz nicht ganz geschlossen werden! Bei größeren Diskrepanzen empfiehlt sich Wahl kleinerer Zeitintervalle, bzw. eine Verfeinerung der Berechnung mit FTSTEPS.
Wird die Fluidmasse (FSPEM = 2,3,4) bei den Berechnungen mit berücksichtigt, nimmt die Bilanzierung eine veränderte Form an:
 |
Die linke Seite von Gl.(11) ist nicht mehr 0, die Masse des Fluids wird zusätzlich Bestandteil dieser Gleichung. Die weiteren Berechnungen erfolgen analog zu Gl.(14)ff.
Bei der Berechnung eines ruhenden Fluids (z.B. Bereitschaft-Betrieb des Speichers) muss die Wärmeleitung im Fluid auf jeden Fall berücksichtigt werden (FHC=1), während im Fall eines strömenden Fluids im Speicher eine Vernachlässigung der Wärmeleitung im Fluid (FHC=0) gerechtfertigt ist.
Für den Wärmeaustausch zwischen den Fluidelementen im Speicher werden die Stoffwerttafeln des Fluids für die Rechnung der Wärmeleitfähigkeit verwendet.
Zusätzlich kann die Wärmeleitfähigkeit mit einem Faktor CLMFL multipliziert werden. Das kann z.B. im Fall der freien Konvektion im Speicher erforderlich sein.
Am Anfang einer Zeitreihenberechnung muss als Anfangsbedingung ein Temperaturfeld des Speichers definiert werden. Die Initiierung kann zu jeder Zeit durchgeführt werden, in dem FINIT=1 gesetzt wird. Hierzu gibt es abhängig von FSTART zwei Möglichkeiten die im Folgenden diskutiert werden:
FSTART=1: Das Temperaturfeld wird im ersten Zeitschritt bzw. bei FINIT=1 homogen zu TSTART gesetzt.
FSTART=2: Im Initiierungszeitschritt gekennzeichnet durch FINIT=1 wird im Inneren des Rohrs ein konstantes homogenes Temperaturprofil des Fluids vom Betrag der Temperatur auf der Eintrittsleitung angenommen. Gegeben ist die Umgebungstemperatur, die Rohrdicke, die Wärmeleitfähigkeit des Rohrs LAM und die Wärmeübergangskoeffizienten ALPHI und ALPHO, mit diesen wird die Temperaturverteilung für diesen stationären Zustand berechnet.
Je nachdem, wie das Problem aufgesetzt ist, kann es zu sehr langen Rechenzeiten bei der Initialisierung kommen. Um dies zu steuern und optimieren zu können, kann der Anwender über folgende Vorgabewerte Einfluss auf die Simulation nehmen:
FTSTEPS, ISUBMAX, IERRMAX, TISTEP
Wie erwähnt, ist die Initialisierung der Simulation eine Berechnung der Lösung für t->inf. In der Praxis muss hier in Bezug auf Genauigkeit und Rechenzeit stets ein Kompromiss gefunden werden. Damit im Zeitreihendialog nicht unnötig viele Zeilen mit den Zeitschritten dieser Berechnungen auftauchen, werden diese Schritte modellintern durchgeführt und nur deren Endergebnis nach Erreichen der Abbruchkriterien angezeigt. Mit ISUBMAX kann die maximale Anzahl dieser Rechenschritte begrenzt werden (i.d.R. sollten nicht mehr als 1000 erforderlich sein.) und zusätzlich kann der numerische Fehler, dargestellt in der Ergebnisvariable PREC (Vergleich der von den Fluiden aufgenommenen, bzw. abgegebenen Wärmeströme mit denjenigen durch die Speicherwände -> konvergiert für die stationäre Lösung, beinhaltet aber stets einen numerischen "Restfehler"!) Über IERRMAX kann hierfür eine Grenze festgelegt werden, bei deren Unterschreiten (i.d.R. 10-6 ausreichend) die Rechnung abgebrochen wird.
Mit FTSTEPS und TISTEP kann das Konvergenzverhalten gesteuert werden. Zum einen kann die Zeitschrittweite über die Gitterkennzahlen bestimmt werden, zum anderen erlaubt eine Vorgabe des Zeitschrittes eine individuelle Anpassung. Bei der Wahl der Schrittweiten ist zu beachten, dass zu große Werte zu oszillierenden oder gar divergierenden Lösungen führen können, an dieser Stelle sei auf die Warnungen, bzw. Fehleranzeigen verwiesen, TSUBREC liefert hier einen zusätzlichen Anhaltspunkt.
Der Vorgabewert TISTEP wird immer auch in der eigentlichen instationären Rechnung verwendet. Ist dieser größer als die von Zeitreihendialog vorgegebene Schrittweite, so wird innerhalb der Komponente nur dieser eine Zeitschritt gerechnet. Ist TISTEP kleiner, führt dies ebenso, wie bei der Initialisierung zur Berechnung von modellinternen (Unter-)Zeitschritten (Ergebniswert ISUB), deren Zwischenergebnisse nicht angezeigt werden.
FINST=0: Die Zeitschrittweite der einzelnen Rechenschritte ist durch die Zeitreihe vorgegeben. Die Berechnung erfolgt ausschließlich mithilfe des Rechenbefehl im Zeitreihenmenü.
FINST=1: Die Berechnung ist stationär, so dass kein Wärmeübergang im Rohr stattfindet. Das Bauteil leitet das Fluid ohne jegliche Berechnung hindurch und ist praktisch ausgeschaltet.
FINST=2: Es erfolgt eine instationäre Einzelrechnung mit der Zeitschrittweite TIMESING. Der Befehl erfolgt mithilfe des Simulationsbefehls aus der EBSILON-Oberfläche.
Es erfolgt eine instationäre Einzelrechnung mit der Zeitschrittweite gemäß den Modelleinstellungen (Simulation > Transient > Behandlung zeitabhängiger Vorgänge Zustand nach vorgegebener Zeit aus Maximaler Zeitschritt). Die Rechnung erfolgt mithilfe des Simulationsbefehls aus der EBSILON-Oberfläche.
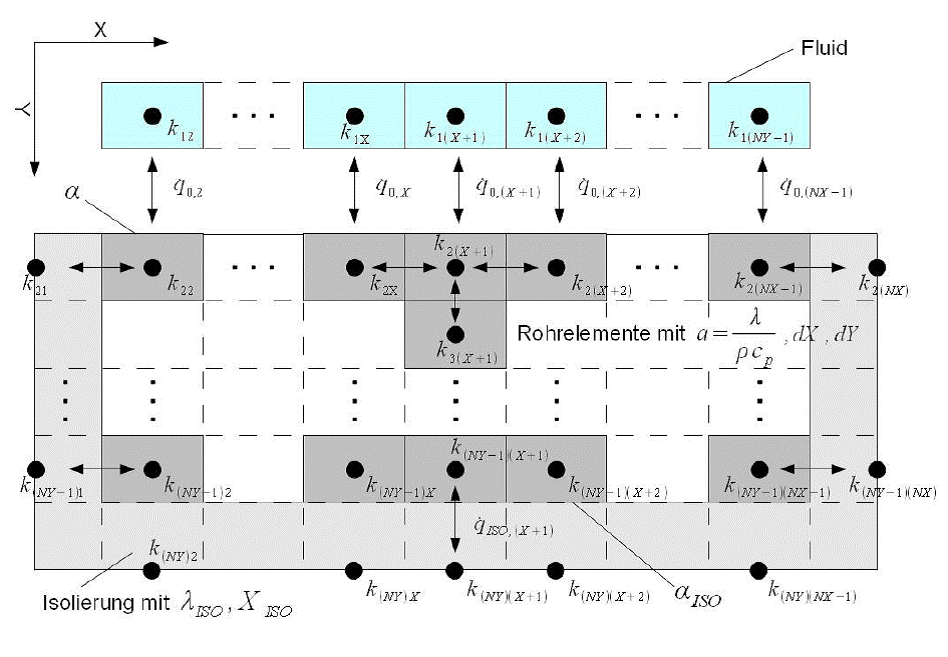
Abbildung 2: Internes numerisches Gitter des Speicherbauteils
Alle transienten Bauteile, die über den Schalter FINIT verfügen, können über einen globalen Schalter gemeinsam gesteuert werden. Dazu wurde der Schalter FINIT um die
Stellung GLOBAL: 0 erweitert.
Wird er auf diesen Wert gesetzt, so übergibt man die Steuerung der transienten Simulation an die globale Variable „Instationärer Modus“, welche unter
Extras \Modell-Einstellungen\Simulation\Kombobox "Instationärer Modus"
zu finden ist.
Diese gibt dann den gewünschten Modus (Erster Durchlauf oder Folgedurchlauf) an die Bauteile weiter. Mit Hilfe des Ausdrucks „@calcoptions.sim.transientmode“ kann dieser
vom Zeitreihendialog aus gesteuert werden.
Zur Vorgabe temperaturabhängiger Materialparameter existieren 3 Kennlinien:
Die übrigen "Kennlinien" dienen der Koppelung der Zeitschritte untereinander und brauchen i.d.R. vom Anwender nicht beeinflusst werden.
Korrespondierend mit diesen "Kennlinien" gibt es zu jeder Ausgabegröße ein Ergebnisfeld.
Spezifikations-Matrix MXTSTO und Ergebnis-Matrix RXTSTO
Die Matrix MXTSTO ist mit der Ergebnismatrix RXTSTO auf die gleiche Weise verknüpft wie die oben genannten Kennlinien und Ergebnisfelder (bzw. Ergebniskurven). Die Verteilung der Werte im Speicher und den Fluiden wird in beiden Matrizen (Vorgabematrix MXTSTO für den Zeitschritt t-1 und Ergebnismatrix RXTSTO für den Zeitschritt t) abgelegt.
Aufbau der Matrizen siehe Matrizen bei BT 119.
|
Form 1 |
Klicken Sie hier >> Bauteil 119 Demo << um ein Beispiel zu laden.