Vorwärmerberechnung gemäß Rabek-Methode

Vorwärmermodell

1.  Problemstellung und Motivation

Das  im Rahmen von Bauteil 10 (FRABEK =0) verwendete Berechnungsmodell geht im wesentlichen davon aus, dass Überhitzungen des Kondensationsdampfes auf die Wärmeübertragung dieses Bauteils zu vernachlässigen sind.

 

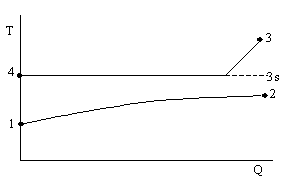
Bild 1: Q-T-Diagramm (bisheriges Modell)

  1:       Eintritt Wasser

  2:       Austritt Wasser

  3:       Eintritt Dampf

  4:       Austritt Kondensat

3s:       Sättigungstemperatur des Druckes P3

Alle Berechnungsbeziehungen benutzen für die Berechnung von Temperaturdifferenzen die Temperatur T_3s. Folgende Nachteile sind mit diesem Modell verbunden:

• Terminal Temperature Difference (T3S-T2) kleiner als 0,5 ^oC (also auch negative Terminal Temperature Differences) führen zu extrem hohen (k x A) - Werten und bilden somit Teillastwerte nicht richtig ab.
• Bei Dampfüberhitzungen im Teillastbetrieb werden die Terminal Temperature Differences nicht korrekt vorhergesagt.

Um Aufgabenstellungen dieser Art zu lösen, musste ein Enthitzer als weiteres Bauteil vorgeschaltet werden.

 

2.  Lösungsvorschlag

Um diese Probleme grundsätzlich zu lösen, muss eine Aufteilung der Flächen im Vorwärmer in Enthitzer- und Kondensatorteil vorgenommen werden, die sich im Teillastfall in Abhängigkeit der thermodynamischen Bedingungen verschieben kann. Rabek hatte eine Methode veröffentlicht (G. Rabek; Die Ermittlung der Betriebsverhältnisse von Speisewasservorwärmern bei verschiedenen Belastungen, Energie und Technik, 1963), die als Grundlage verwendet wird. Von dieser Arbeit werden folgende Aspekte übernommen:

• das Modell für Enthitzer und Kondensatorteil
• die k - Zahl Berechnungsmethode

Nicht übernommen wurde:

• Die Integration des Vorwärmers in das Bauteil, da diese Erweiterung nicht notwendig ist. Änderungen dieser Art sind späteren Modifikationen vorbehalten.
• Die Berechnungsmethodik und die Auflösung des Gleichungssystems.

Basis des verwendeten Modells stellt die Aufteilung in Kondensatoranteil (I) und Überhitzeranteil (II) dar (Bild 2).

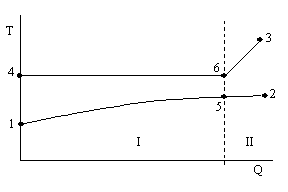
Bild 2: Q-T-Diagramm (neues Modell)

1:         Eintritt Wasser

2:         Austritt Wasser

3:         Eintritt Dampf

4:         Austritt Kondensat

5:         Zwischenpunkt Wasser

6:         Kondensationsbeginn Dampf

I:          Kondensationsbereich

II:         Enthitzerbereich

 

Folgende Beziehungen beschreiben die Wärmeübertragungsverhältnisse exakt

            Q = Q_I + Q_II                                                                  (1)

            Q = k_I A_I Dt_mI + k_II A_II Dt_mII                                             (2)

Q:        übertragene Wärmemenge

k:         k - Zahl für Bereiche I und II

A:        Fläche

Dtm:    logarithmische Temperaturdifferenz

 

Bekannt ist das Verhältnis Q_I/Q_II aus der Dampfenergiebilanz sowie die logarithmische Temperaturdifferenz, da alle Temperaturen berechnet werden können.

Aus (2) ergibt sich

            Q = k_I A_I  Dt_mI (1 + Q_II/Q_I)                                               (3)

sowie

            Q_I/Q_II = (k_I A_I Dt_mI) / (k_II A_II Dt_mII)                                     (4)

 

(4) umgestellt führt zu

            A_II/A_I = Q_II /Q_I Dt_mI/Dt_mII k_I/k_II                                           (5)

Die Gesamtfläche A setzt sich zusammen

            A = A_I + A_II = A_I (1 + A_II/A_I)                                               (6)

oder

            A_I = A / (1 + A_II/A_I)                                                            (7)

 

Die übertragene Wärmemenge nach (2) kann somit geschrieben werden als

            Q = (k_IA) / (1+A_II/A_I) (1+Q_II/Q_I) Dt_mI                                   (8)

 

(k_I A) stellt die bekannte Größe WTKF dar; Q_II/Q_I ergibt aus der Wärmebilanz

Dampf und A_II / A_I kann aus (5) bestimmt werden.

Zur Nutzung der Gleichung (8) müssen noch Beziehungen für

            - k_I    sowie

            - k_I / k_II

für Voll- und Teillast hergeleitet werden.

Zur Entwicklung dieser Beziehungen wird eine Terminologie wiederum nach Rabek verwendet.

            k_I / k_Iv = (1/a_1v + 1/a_3v) / (1/a₁ + 1/a₃)                                (9)

            a₁: a-Zahl Wasser (Leitung 1)

            a₃: a-Zahl Dampf ( Leitung 3)

            Index v: Volllast

            mit

            b = a_1v / a_3v         und                                                        (10)

            g₁ = a₁ / a_1v         sowie                                                        (11)

            g₃ = g₃ / a_3v                                                                       (12)

            ergibt sich

            k_I/k_Iv = g₃(1+b) / (g₃/g₁+b)                                                  (13)

Das k - Zahl Verhältnis k_I / k_II kann wie folgt formuliert werden.

            k_I/k_II = k_Iv/k_IIv k_I/k_Iv 1/(k_II/k_IIv)                                              (14)

Mit (10) und (11) ergibt sich

            k_Iv/k_IIv = (a1_IIv /a1_Iv) (1+b_II) / (1+b_I)                                     (15)

Das Verhältnis der a₁ - Zahlen kann zu 1 gesetzt werden.

Für die Verhältnisse k_I / k_IV und k_II / k_IIV gilt

            k_I/k_Iv = g_1I(1+b_I) / (1+g_1I / g_3Ib_I)                                            (16)

            k_II/k_IIv = g_1II(1+b_II) / (1+g_1II/g_3IIb₂)                                         (17)

Mit g_1I » g_1II (gleiches Medium) und g_1II » g_3II (einphasiges Medium) gilt

            k_I/k_II = (1+b_II) / (1+b_I) (1+b_I) / (1+g_1I/g_3I b_I)                            (18)

Die g - Abhängigkeiten werden den Angaben von Rabek entnommen.

            g_1I = (m_1I/m_1vI)^0,8                                                                  (19)

            g_3I = (m_3I/m_3vI)^0,33                                                                 (20)

Mit (18) bis (20) ist das System geschlossen lösbar.

 

3.  Berechnungsgang

Volllastrechnungen (Last = 0, IFAL = 0) basieren auf Vorgabe einer (auch negativen) Terminal Temperature Difference, die aus numerischen Gründen auf -10 K begrenzt ist. Mit Vorgabe dieser Terminal Temperature Difference werden alle Temperaturen bestimmt, A_II / A_I (5) sowie Q_II / Q_I berechnet. Aus der Wärmeübertragungsbeziehung (8) und den beiden Bilanzgleichungen für jedes Fluid werden Massenstrom m₃ und k_I x A bestimmt.

Im Teillastfall werden bei gegebenem k_I A  m₃ sowie alle Temperaturen berechnet, wobei die Teillastbeziehungen (15) sowie (18) - (20) benutzt werden.

Die Wärmeübergangsflächen A_I (Kondensator) und A_II (Überhitzer) können sich soweit bei konstanter Gesamtfläche A in Abhängigkeit der thermodynamischen Bedingungen verschieben.

 

4.  Anwendung

Um das neue Modell zu nutzen, muss eine Kontroll - Variable im Definitionsmenü verändert werden.

 

Teillastfunktionen nach Rabek

1.  k-Zahl - Verhältnis

k/k0 = (1/a10 + 1/a30) / (1/a1 + 1/a3) = (1 + (a10/a30)) / ((a10/a1) + (a10/a30) (a30/a))

mit

            a₁₀/a₃₀ = b
            a₁/a₁₀ = g₁   ;   a₃/a₃₀ = g₃ 

k/k₀ = (1+b) / (1/g₁ + b/g₃)
k/k₀ = g₃ (1 + b) / ((g₃/g₁) + b)                                                               (21)

 

 2.  Enthitzer / Verdampfer-k-Zahl

k_I/k_II = k_v/k_E = k_v0/k_E0  k_v/k_v0  1/(k_E/k_E0)

k_v0/k_E0 = (1/a_1E + 1/a_3E) / (1/a_1v + 1/a_3v) = a_1E/a_1v (1 + b_E) / (1 + b_v)        (22)

(k_v/k_v0) (1/(k_E/k_E0) = g₁(1 + b_v) (1 + (g₁b_E/g₃)) / (1 + (g₁b_v/g₃)) g₁ (1+b_E) 

                                =  (1 + b_v) / (1 + (g₁b_v/g₃))                                       (23) 

k_I/k_II = k_v/k_E = (1+b_E) / (1+b_v) (1+b_v) / (1+(g₁b_v/g₃))                                 (24)

 

3.  Typische Werte nach Rabek 

g₃ ~ (m₃/m₀₃)^0,33    sowie   m₃/m₁ ~ m₃₀/m₁₀
g₁ ~ (m₁/m₀₁)^0,8
b_E ~ 15
b_v ~ 2 

aus (1)            k/k₀ = (m₃/m₃₀)^0,33   3/((m₃/m_v)^-0,5 + 2)                                (25)

aus (4)            k_I/k_II = k_v/k_E = 16/3 (1+2) / (1+ (m₃/m₃₀)^0,5  2)                     (26)