Grundlagen der Modellierung

Ein Kraftwerk besteht aus verfahrenstechnischer Sicht aus Komponenten, die durch Leitungen miteinander verbunden sind. Der Energietransport geschieht durch sogenannte Fluide (Wasser, Wasserdampf, Rauchgas, Luft etc.), deren Zustandsgleichungen in Form von standardisierten Polynomen vorliegen.

Eine exakte thermohydraulische Modellierung der jeweils anstehenden Lastpunkte des realen Kraftwerks würde es gestatten, die Fehler der gerade vorliegenden Messwerte auszuweisen. Die heute verfügbaren stationären Simulationsprogramme, die bislang schon für Planungs- und Auslegungsrechnungen eingesetzt wurden, ermöglichen im Hinblick auf die Massen- und Energiebilanzierung eine hohe Modellierungsgenauigkeit, wobei bestimmte Parameter in den physikalischen Komponentengleichungen durch Kennlinien bzw. Kennflächen beschrieben werden, die das reale Verhalten hinreichend genau darstellen. Im Hinblick auf die Datenvalidierung nach der Richtlinie VDI 2048 sind neben deren Ungenauigkeiten zusätzlich solche in verwendeten Gleichungen (z.B. Dampfkegelgesetz) und Daten zu berücksichtigen.

Wird eine Detektierung von Messfehlern im Prozentbereich erwartet, so sollte die Genauigkeit des Rechenmodells dem entsprechen, denn sonst könnte die Differenz aus Messwert und gerechnetem Wert auch auf Modellierungsungenauigkeiten zurückzuführen sein. Bevor also Datenvalidierung sinnvoll betrieben werden kann, muss die Tauglichkeit des Rechenmodells und der vorgesehenen Auswertungen nachgewiesen werden. Dabei sind die Forderungen des Kriterienkatalogs des VDI für die Zertifizierung zu erfüllen und das System der Nebenbedingungen bezüglich eventueller Unzulänglichkeiten bzw. Ungenauigkeiten zu durchleuchten. Die Nebenbedingungen werden automatisch aus der mit der EBSILON^®Professional-Benutzeroberfläche erstellten Modelltopologie und den Bauteil-Spezifikationen abgeleitet. Die generierten Bilanzgleichungen können formal als korrekt angesehen werden, da EBSILON diesbezüglich seit Jahren fehlerfrei arbeitet. Jedoch ist in Betracht zu ziehen, dass Unzulänglichkeiten in der Modellierung zu Widersprüchen führen (z.B. Vernachlässigung von Leckströmen). Daher sind Bilanzverletzungen bereits mit den Rohwerten zu prüfen (s. Fehleranalyse).

Die für die einzelnen Bauteile verwendeten Gleichungen können über Mausklick aus der Systemhilfe aufgerufen und angezeigt werden. Dies soll beispielhaft am Hilfetext zur Dampfturbine (Bauteil 6). erläutert werden. Mit der Vereinfachung, dass der mechanische Wirkungsgrad ETAMN=1 und Eintritts- und Austrittsverluste DH1LN=DH2LN=0 sind, lassen sich die angegebenen Gleichungen folgendermaßen zusammenfassen:

erläutert werden. Mit der Vereinfachung, dass der mechanische Wirkungsgrad ETAMN=1 und Eintritts- und Austrittsverluste DH1LN=DH2LN=0 sind, lassen sich die angegebenen Gleichungen folgendermaßen zusammenfassen: 

(1)  P1 = SQRT (P2^2 + ((M1/M1N)^2)*(V1/V1N)*(P1N^2-P2N^2) )   (Dampfkegelgesetz nach Stodola)  Siehe dazu: Turbinen - Teillast Berechnung - Stodola 

(2)  P3 = P2

(3)  P4 = P2

(4)  H2 = H1 - (H1 - H2S) * ETAI   , wobei sich H2S aus P2 und S1 aus der Wasserdampftafel ergibt

(5)  H3 = H2

(6)  H4 = H2

(7)  Q6 = Q5 + M1 * (H1 - H2)     (Energiebilanz, Verluste vernachlässigt)

(8)  M2 = M1 - M3 - M4                (Massenbilanz, Verluste vernachlässigt)

Mi, Pi, Hi, Vi, Si, Qi sind Massenstrom, Druck, spezifische Enthalpie, spezifisches Volumen, Entropie und Leistung am Anschluss i der Komponente (wie im folgenden Bild angezeigt, entsprechend der EBSILON-Anschlussbenennung). Der Einfachheit halber sind Verluste in der Massen- und Energiebilanz vernachlässigt, die bei einer Abbildung einer realen Anlage natürlich zu berücksichtigen sind (z.B. Abzweigungen an den Austritten 2, 3 oder 4).

Da das Dampfkegelgesetz nicht streng gilt, kann es auch aus den Nebenbedingungen herausgenommen werden, in dem man bei der Turbine den Schalter FP1N auf "P1 von außen gegeben" stellt. Es wird dann der Messwert in der Anzapfung als Vorgabewert verwendet. Liegt ein solcher nicht vor, so kann ein Pseudomesswert angelegt werden, dessen Belegung aus der Simulationsrechnung mit Stodola gewonnen wird. Das zugehörige Konfidenzintervall ist entsprechend der vermuteten Unsicherheit anzusetzen. Bei einer nennenswerten Durchsatzänderung in der Validierung kann eine iterative Behandlung der Druckvorgabe notwendig werden, was durch Simulationsrechnungen mit validierten Werten vorgenommen werden kann. Dabei sollte der Expansionsverlauf über die gesamte Turbinenstufe (siehe h,s-Diagramm) beachtet werden.

Um einen Überblick über die verwendeten Gleichungen (Darstellung der Nebenbedingungen in Bilanzform) zu erhalten, kann man die Gleichungsliste aufschalten

In den Bauteilgleichungen sind allerdings Spezifikationsdaten enthalten, die unzutreffend sein können. Dies zeigt das folgende Simulationsbeispiel:

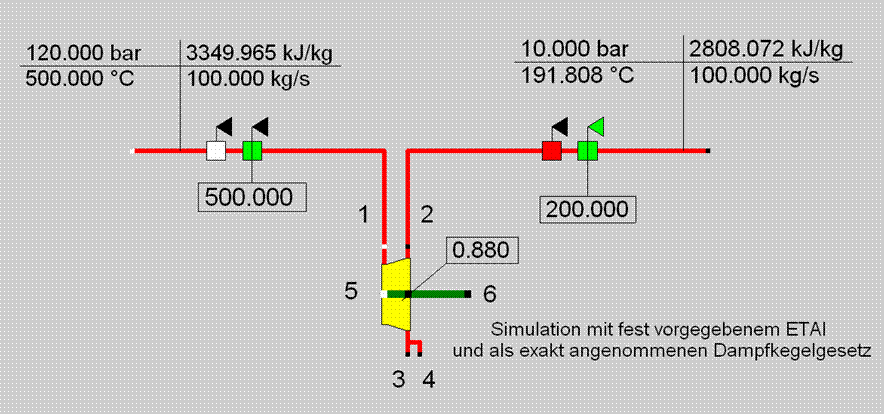
Bauteil 6- Schaltung mit falschem ETAI

Die Gleichungen wurden korrekt generiert, aber die Abweichung der gerechneten Austrittstemperatur (191.8 °C) von ihrem Messwert (200 °C) deutet eine unzutreffende Spezifikation des isentropen Wirkungsgrades (ETAI) an. Auf diese Weise können bereits durch eine Simulation mit den Rohdaten Unstimmigkeiten aufgedeckt werden. In einer Validierungsrechnung müssen dann alle Unsicherheiten in Betracht gezogen werden, d.h. Größen wie ETAI und Verluste müssen mit validiert werden. Hier soll aber nur auf den Nutzen der vorausgegangenen Simulation eingegangen werden.

Im Beispiel kann das Bauteil im Identifikationsmodus den zutreffenden ETAI-Wert aus der Austrittstemperatur-Messung ableiten:

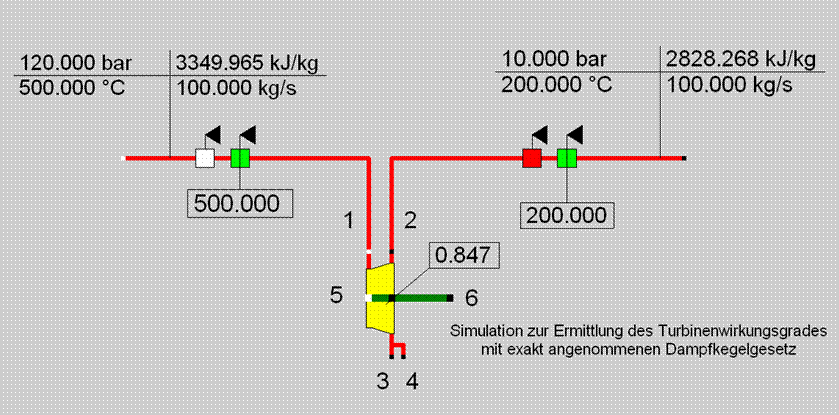
Bauteil 6-Schaltung mit ETAI-Berechnung

Sollte die Austrittstemperatur falsch gemessen worden sein, so wird dies in den Ergebnissen des Folgebauteils zum Ausdruck kommen. Die Simulationsergebnisse für die Gesamtschaltung stellen also eine wertvolle Hilfe zur Überprüfung von Messwerten und Modell dar.

Wenn in der Umgebung einer Komponente Messwerte stark von den gerechneten Werten abweichen, so kommen als Ursache neben einer fehlerhaften Messwertnahme in Betracht: falsche Parametrierung der Komponente, unzutreffende Wahl der Komponente oder Verletzung der verwendeten Gleichungen (Nebenbedingungen), was vielleicht auf einen Schaden der Komponente zurückzuführen ist.

Am Beispiel des Dampfkegelgesetzes soll der Sachverhalt verdeutlicht werden. Für die Druckberechnung in einer Dampfturbinenscheibe sei über die Spezifikationsmaske das Dampfkegelgesetz in der folgenden Form gewählt worden:
p1^2 = p2^2 + ((m1/m1n)^2)*(v1/v1n)*(p1n^2-p2n^2)       (die Bedeutung der Zeichen kann der Bauteilhilfe entnommen werden)
Die Gleichung hat volle Gültigkeit bei Nennlast im Auslegungspunkt, während in Teillast die Genauigkeit nachlässt. Alle Größen der Gleichung und diese selbst müssen als fehlerhaft betrachtet werden. Während p1, m1, v1 mit ihren Unsicherheiten unmittelbar in die Ausgleichsrechnung eingehen, ist dies für die Nennwerte nicht gegeben, zumal diese nicht fest, sondern teillastabhängig sind, d.h. die wahren Nennwerte existieren eigentlich nicht. Unter Beachtung der Unsicherheit der Nenngrößen und der Formel selbst wird für den Rechenwert p2 ein angemessenes Konfidenzintervall angesetzt und für p2 der in der Simulation mit dem Dampfkegelgesetz berechnete Wert als Schätzwert in einem Pseudomesswert eingetragen. In der Validierung wird dann das Dampfkegelgesetz ausgeschaltet und der Pseudomesswert als validierungsfähiger Vorgabewert verwendet. Besteht zwischen dem gerechneten p2 und einem eventuell gemessenen Anzapfdruck eine zu große Differenz, so muss entweder bei zu vermutendem Druckverlust auf dem Wege bis zum Messpunkt dieser Druckverlust validierungsfähig modelliert werden (am zugehörigen Vorwärmer muss die Kondensat-Sättigungstemperatur im Einklang stehen), oder die Nennwerte der Turbine modifiziert werden. Werden Drucknennwerte geändert, so ist aber dabei darauf zu achten, dass der Turbinenwirkungsgrad (validierbar) nicht unzulässige Werte annimmt, was im überhitzten Dampfbereich bei einer vertrauenswürdigen Messung der Austrittstemperatur (validierbar) zu einem anderen Widerspruch führen würde. Die Parametrierung des Kraftwerkmodells erfordert, wie dieses Beispiel zeigt, besondere Sorgfalt. Natürlich sind die Betrachtungen bei Massen- und Energie-Bilanzen einfacher. Bei bestehender Notwendigkeit können hier Abweichungen (z.B. bei Wärmeverlust an einer als adiabatisch durchströmt angenommenen Komponente) mit einfachen Mitteln validierbar modelliert werden.

Die Überprüfung des Rechenmodells kann einerseits durch Vergleich mit den präzisen Auslegungsrechnungen der Lieferanten für die Komponenten und die Gesamtanlage geschehen, andererseits können korrigierte Abnahme- und Präzisionsmessungen an Komponenten herangezogen werden. Die Anpassung der Spezifikationsparameter und Kennlinien sollte schließlich zu der erforderlichen Genauigkeit führen.

Ist dieses Ziel erreicht, kann mit der Datenvalidierung begonnen werden. Um das Gleichungssystem des Modells lösen zu können, genügt die Vorgabe von einigen kreislaufdefinierenden Messwerten (Drücke, Temperaturen, Massenströme). Die Rechnung liefert das thermodynamische Prozessabbild, bestehend aus Komponenten- und Leitungsdaten. Wegen der Fehlerhaftigkeit lässt man aber mehr - am besten alle - Messwerte in die Auswertung einfließen. Es ergibt sich so ein überbestimmtes Gleichungssystem, das mit der Methode der kleinsten Fehlerquadratsumme auf ein bestimmtes zurückgeführt werden kann, dessen symmetrische Matrix in einfacher Auflösung die validierten Messwerte ergibt. Die Einhaltung der Massen- und Energiebilanzen für die Komponenten und die Gesamtanlage muss dabei als Nebenbedingung in der Anpassungsrechnung berücksichtigt werden. Das am Modell validierte Prozessabbild stellt im Sinne des Verfahrens den wahrscheinlichsten Prozesszustand dar, d. h. die Differenzen zwischen den Messwerten und den zugehörigen validierten Werten geben die wahrscheinlichen Fehler (mit Vorzeichen) der Messwerte an.