

|
Leitungsanschlüsse |
|
|
|
1 |
Dampf-Eintritt |
|
|
2 |
Damp-Austritt |
|
|
3 |
Anzapfung 1 |
|
|
4 |
Anzapfung 2 Dampf /KEINE |
|
|
5 (8) |
Welleneintritt Welle/KEINE |
|
|
6 |
Wellenaustritt Welle /KEINE |
|
|
7 |
Regeleingang für Wirkungsgrad (als H) Regeleingang /KEINE |
|
|
8 |
Wellenaustritt Welle /KEINE |
|
Allgemeines Wellenanschluss Berechnung Totaler vs statischer isentroper Wirkungsgrad Vorgabewerte Kennlinien Bauteilphysik Ergebnisse Bauteilform Beispiel
Bauteil 6 dient zum Zweck der Umwandlung von thermischer bzw. potentieller Energie eines Prozessstroms in mechanische Energie auf einer Welle. Er kann auf Wasser (nicht komprimierbare Strömung, hydraulische Turbine), oder auf Dampf bzw. jedes andere Fluid des Typs Gas, Rauchgas, Universalfluid oder Zweiphasenfluid flüssig/gasförmig angewendet werden (komprimierbare Strömung, Turbomaschine). Als solches ist er die vielseitigste Komponente in EBSILON um die Energieumwandlung durch die Expansion eines Prozessstroms zu modellieren.
Bauteil 6 stellt eine einzelne Expansionsstufe, eine Stufengruppe oder eine kompletten Abschnitt der modellierten Maschine dar. Eine Entnahme oder Zuführung im Laufe des Expansionsprozesses muss durch die Verwendung mehrerer aneinander gereihter Bauteile 6 modelliert werden. Zuführungen müssen durch Mischer in die Verbindungsleitung zwischen zwei benachbarten Bauteilen 6 abgebildet werden. Entnahmen können durch die Anschlüsse 3 oder/und 4 modelliert werden, die hinzugefügt wurden, um die Notwendigkeit der Verwendung zusätzlicher Verzweigungen zu reduzieren.
Früher war der zweite Wellenanschluss bei Bauteil 6 (Dampfturbine) ein Welleneingang. Dadurch war es bei Bauteil 6 möglich, mehrere Turbinenscheiben hintereinander zu schalten, so dass sich die Wellenleistung addierten.
Der umgekehrte Fall Leistungsaufteilung bei Bauteil 6 konnte grafisch früher nicht dargestellt werden. Allerdings gab es zur Berechnung einen Schalter FQ (Leistungsfluss), mit der die Berechnung umgestellt werden konnte, allerdings mit der Unschönheit, dass die grafische Darstellung dann nicht zur Berechnung passte.
Mittlerweile kann der umgekehrten Leistungsfluss auch grafisch abgebildet werden. Hierfür ist der Wellenanschluss 8 zu nutzen.
Um eine entsprechende Darstellung zu ermöglichen, wurde der früher vorhandene Anschluss ausblendbar gemacht und der neue Anschluss wurde an derselben Stelle positioniert. Üblicherweise wird man ja entweder den Eingang oder den Ausgang benutzen und sollte dann den nicht genutzten Anschluss ausblenden. Prinzipiell ermöglicht die Software aber auch die gleichzeitige Nutzung beider Anschlüsse.
Wie beim bisherigen zweiten Wellenanschluss muss auch auf dem neuem Anschluss die Leistung vorgegeben werden. Die Turbine kann nur die Leistung am Haupt-Wellenausgang berechnen.
Durch den neuen Anschluss ist der Schalter FQ jetzt überflüssig. Aus Kompatibilitätsgründen ist er allerdings weiterhin verfügbar, wurde aber als „veraltet“ gekennzeichnet.
Außerdem wird gegebenenfalls eine Kommentarmeldung ausgegeben, der auf die Möglichkeit zur Nutzung des neuen Anschlusses hinweist. Für den neuen Wellenanschluss bewirkt der Schalter ebenfalls eine Umkehr der Berechnungsrichtung.
Beim Bauteil 6 (auch beim Bauteil 23, 58) wurde ein neuer Ergebniswert QSHAFT implementiert, der die im Bauteil erzeugte Wellenleistung ausgibt, unabhängig davon, auf welche Anschlüsse sie sich verteilt oder welche Wellenleistung noch hinzukommt.
Die Berechnungen der Dampfturbine haben zwei Ziele:
Die Durchflusscharakteristik (Eintrittsdruck als Funktion des Massenstroms) wird mit Hilfe des Kegelgesetzes von Stodola bestimmt.
und dem Durchflusskoeffizienten, der folgendermaßen definiert ist
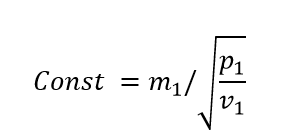
und in allen Betriebszuständen konstant ist.
In dieser Gleichung bezeichnen m1 den Eintrittsmassenstrom, p1 den Eintrittsdruck und v1 das spezifische Volumen am Eintritt.
Im Auslegungsmodus wird der Durchflusskoeffizient unter Verwendung der Benutzervorgaben (bzw. Bilanzergebnisse) für Massenstrom, Druck und spezifischem Volumen. Der Benutzer kann zwischen zwei Methoden zur Vorgabe des Eintrittsdrucks auswählen:
Der Austrittsdruck P2 wird immer durch externe Komponenten vorgegeben. Eine solche externe Komponente kann z.B. die nachfolgende Expansionsstufe sein, ein nachgeschalteter Kondensator oder direkte Vorgaben mittels Bauteil 33 oder 46.
In Teillast berechnet Bauteil 6 den Eintrittsdruck P1 als Funktion des Massenstroms, Austrittsdrucks und dessen spezifischen Volumens aus dem Stodola-Gesetz:
Siehe dazu und auch zur Formulierung des Stodola-Gesetzes : Turbinen - Teillast Berechnung - Stodola
Im Kapitel "Teillast Berechnung der Dampfturbine" bezeichnen M1N, P1N, P2N und V1N die Nominalwerte im Auslegungsfall bzw. M1, P1, P2 und V1 die entsprechenden Größen unter den augenblicklichen Bedingungen. Wie im Auslegungsfall ist auch hier der Austrittsdruck P2 immer durch externe Komponenten bestimmt.
Bauteil 6 verwendet die Methode des isentropen Wirkungsgrads, um die Enthalpiedifferenz zufolge der Expansion zu berechnen.
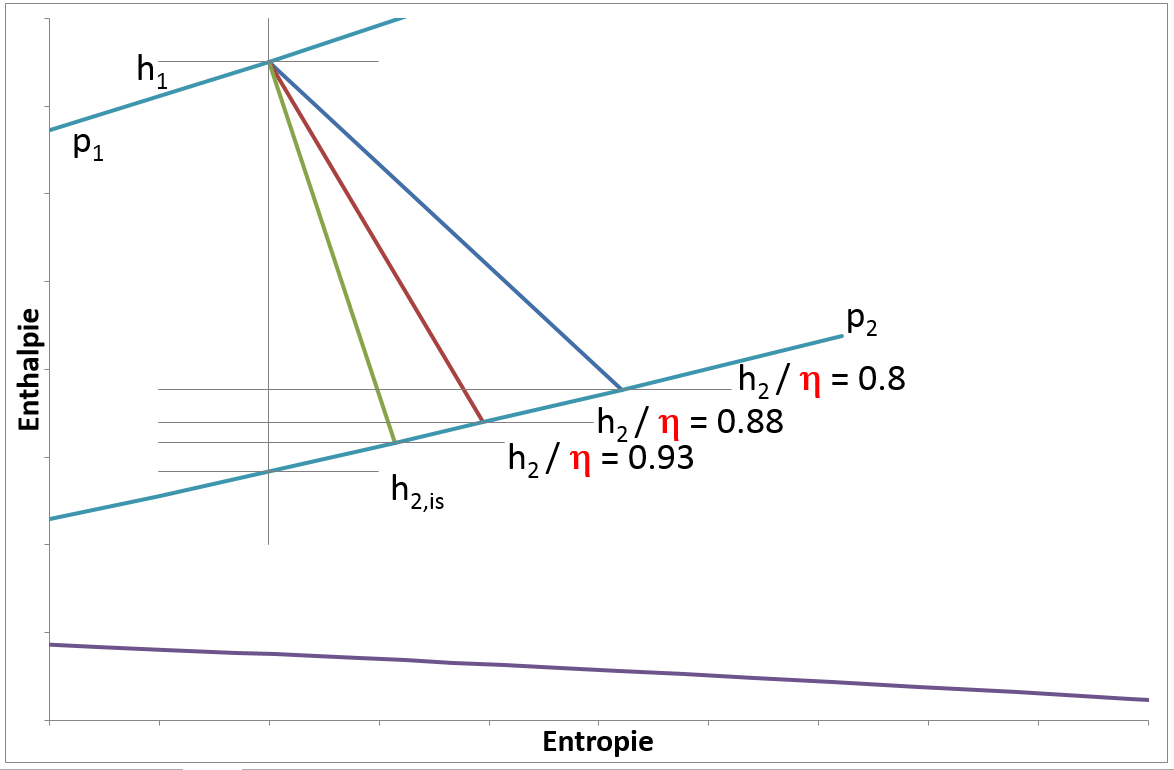
Abbildung 1: Enthalpie-Entropie (H-S) Diagramm einer einzelnen Expansionsstufe.
Die mechanische Leistung der Welle wird dabei folgendermaßen bestimmt:
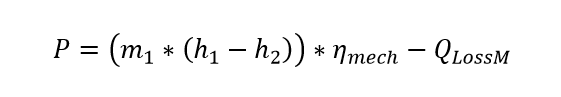
Mit Verwendung des isentropen Wirkungsgrads ergibt sich folgende Gleichung:
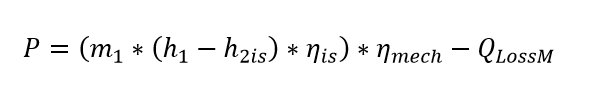
wobei m1 den Eintrittsmassenstrom, h1 und h2 die spez. Enthalpie am Ein- bzw. Austritt und ηis den isentropen Wirkungsgrad bezeichnen und die mechanischen Verluste über QlossM absolut bzw. über ηmech relativ definiert werden. Im Auslegungsfall gibt der Benutzer entweder die Austrittsenthalpie außerhalb von Bauteil 6 mittels den Bauteilen 33 oder 46 vor, oder er setzt den isentropen Wirkungsgrad im Parameter ETAIN. Im Teillastmodus wird der isentrope Wirkungsgrad relativ zum Nominalwert mit Hilfe von Korrekturkurven (Kennlinien) bestimmt, die die Veränderung des Wirkungsgrads mit dem Verhältnis der Massenströme, dem Verhältnis der Volumenströme oder dem Druckverhältnis der Expansion - jeweils relative zum Nominalwert - in Verbindung setzen.
Bisher konnten Identifikationsmodi bei der Dampfturbine durch einen negativen Wert des Schalters für den Kennlinientyp (FCHR) aktiviert werden. Dies ist allerdings nicht nur schwer für den Anwender zu finden, sondern hat auch den Nachteil, dass bei der Ermittlung des Ergebniswertes ETACL nicht bekannt ist, welcher Kennlinientyp verwendet werden sollte. Bisher wurde aus historischen Gründen ETACL zum Kennlinientyp FCHR=0 (massenstromabhängige Kennlinie) berechnet.
Analog zu anderen Bauteilen auch für die Dampfturbine ein Schalter FIDENT eingeführt.
Dieser hat die Einstellungen
Damit sich das Verhalten vorhandener Schaltungen nicht ändert, können die Identifikationsmodi auch weiterhin durch negative FCHR-Einstellungen aktiviert werden.
In diesem Fall wird die FIDENT-Einstellung ignoriert. Darauf wird in einem Kommentar hingewiesen.
Bei Verwendung von FIDENT wird für die Berechnung von ETACL nun der in FCHR eingestellte Kennlinientyp verwendet.
Es ist möglich, zu einer von außen gegebenen Wellenleistung, den dazu benötigten Dampfmassenstrom zu berechnen. Dadurch ist die Modellierung einer Speisewasserpumpe mit Antriebsturbine direkt möglich. Ein Regler musste dazu verwendet werden, um die Antriebsleistung der Pumpe mit der Turbinenleistung in Einklang zu bringen.
Dieser Berechnungsmodus wird aktiviert, in dem der neuen Schalter FSPECQ auf 1 gestellt wird. Er kann allerdings nur für eine einzelne Turbinenscheibe verwendet werden. Wenn mehrere Turbinen und Anzapfungen vorhanden sind, ist ein Regler zur Einstellung einer gewünschten Leistung zu verwenden.
Es ist wichtig anzumerken, dass in EBSILON Stoffwerteaufrufe ohne Bezug auf die Geschwindigkeit des jeweiligen Prozesstroms durchgeführt werden, folglich sind alle Zustandsgrößen basierend auf Totalenthalpie (oder auch Stagnationsenthalpie genannt) zu verstehen. Die dem zu Grunde liegende Konvention ist, dass EBSILON auf Basis von Totalenthalpien arbeitet.
Die Energiebilanz einer Turbomaschine kann nur auf Basis von Totalenthalpien exakt und physikalisch korrekt geschlossen werden, es sei denn, die Strömungsgeschwindigkeiten und Verwirbelungsverluste am Ein- und Austritt sind bekannt. Die Totalenthalpie und die statische Enthalpie eines Stromes hängen folgendermaßen zusammen:
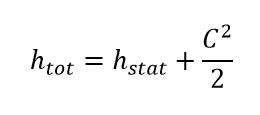
Abbildung 2 zeigt die entsprechende Expansionslinie im H-S-Diagramm, wobei die statischen und totalen Eigenschaften exakt mittels der jeweiligen kinetischen Energie korreliert werden.
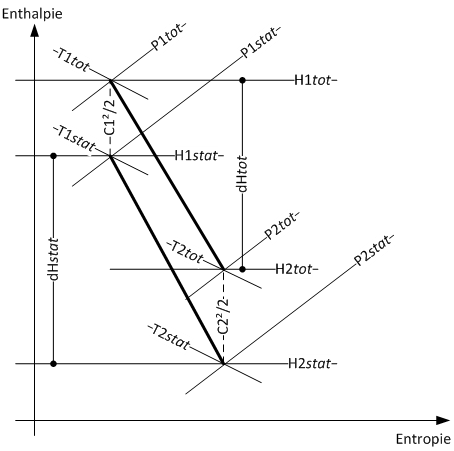
Abbildung 2: Totale und statische Zustände im H-S-Diagramm für Bauteil 6.
Isentrope Wirkungsgrade müssen konsistent ermittelt werden, entweder auf Basis statischer oder totaler Zustände.
In Anwendungen von EBSILON zur Gütegradanalyse, wo die Berechnungen mit Messwerten der Anlage verglichen werden, ist es wichtig zu erkennen, dass Messwerte für Druck und Temperatur in den seltensten Fällen in Form von totalen Werten zur Verfügung stehen sondern üblicherweise als statische Messwerte für Druck und Temperatur. Um es genau zu sagen, diese statischen Messungen müssten mit Hilfe des obigen Zusammenhangs in die entsprechenden (totalen) Stagnationsgrößen umgewandelt werden. Abbildung 3 zeigt eine Energiebilanz, in der auf den Strömen auch die totalen (Stagnations-) Prozessgrößen angezeigt werden.
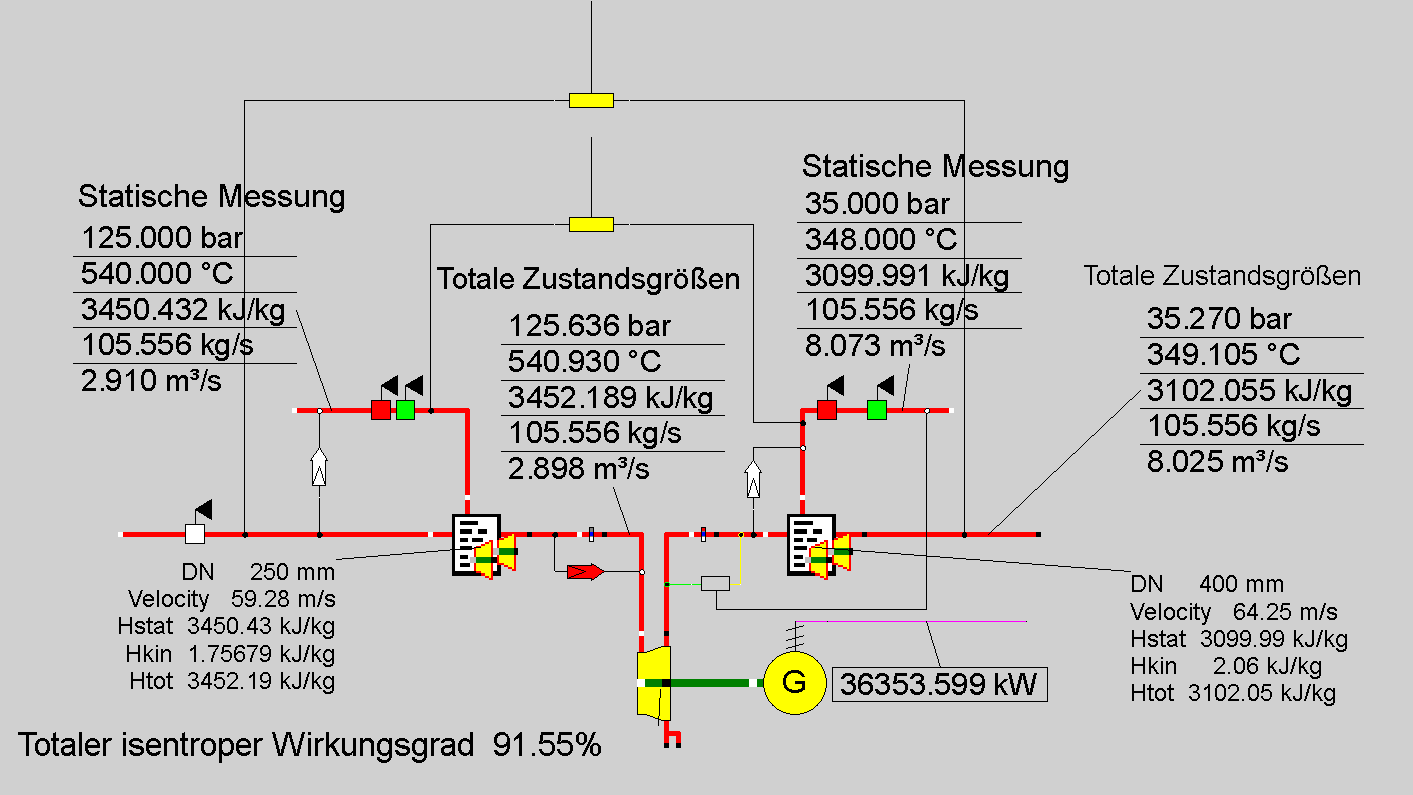
Abbildung 3: Energiebilanz um Bauteil 6 unter Verwendung der exakten Definition von statischen und totalen Zustandsgrößen.
Die Information über die Strömungsgeschwindigkeiten am Messpunkt sind aber wie gesagt selten verfügbar. Für die praktische Anwendung werden daher diese statischen Zustandsgrößen direkt benutzt, um die entsprechenden Enthalpiewerte als Vorgabe in EBSILON zu definieren. Abbildung 4 zeigt dieselbe Energiebilanz, die statische Eingabewerte anstatt totaler Zustandsgrößen für die Ströme rund um Bauteil 6 verwendet.
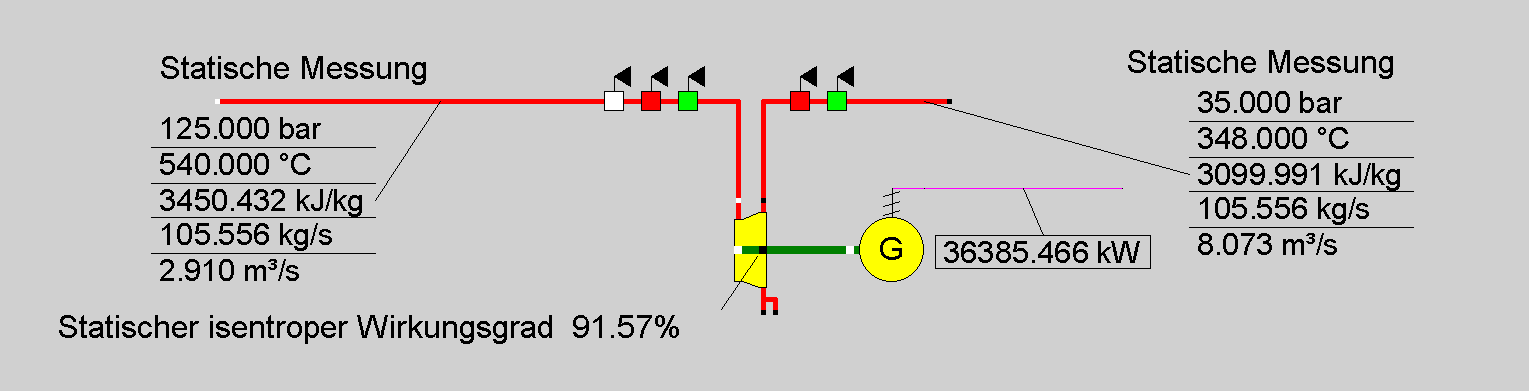
Abbildung 4: Energiebilanz rund um Bauteil 6 unter Verwendung statischer Zustandsgrößen.
Für die typische Anwendung, in der EBSILON eher zur Bewertung von Stufengruppen bzw. Sektionen als zur Überwachung einzelner Stufenwirkungsgrade herangezogen wird, sind die Auswirkungen der Verwendung statischer Zustandsgrößen sehr gering, insbesondere in Relation zum Absolutwert. Typische Auslegungsregeln für Strömungsgeschwindigkeiten in Dampfleitungen und Dampfturbineneinlauf- bzw. Auslaufgehäusen sehen Geschwindigkeiten im Bereich 50 bis 70 m/s vor. Dies gilt sowohl für den Eintritts- wie für den Austrittsbereich, da die Austrittsflansche deutlich größer als jene am Eintritt gebaut werden.
Auf den Zahlenwert der Gütegradanalyse hat die Wahl der Basis für die Zustandsgrößen - ob statisch oder total - numerisch nur minimale Auswirkungen. Die Unsicherheit in den Messwerten für Druck und Temperatur ist zumeist deutlich größer als diese Ungenauigkeit. Abbildung 5 zeigt die Expansionslinien für das gezeigte Beispiel im H-S-Diagramm im Zusammenhang mit den tatsächlichen Proportionen, einmal auf Basis statischer Zustandsgrößen und einmal mit totalen Zustandsgrößen ermittelt. Diese Abbildung zeigt deutlich, dass die Größenordnung dieser Effekte vernachlässigbar klein ist.
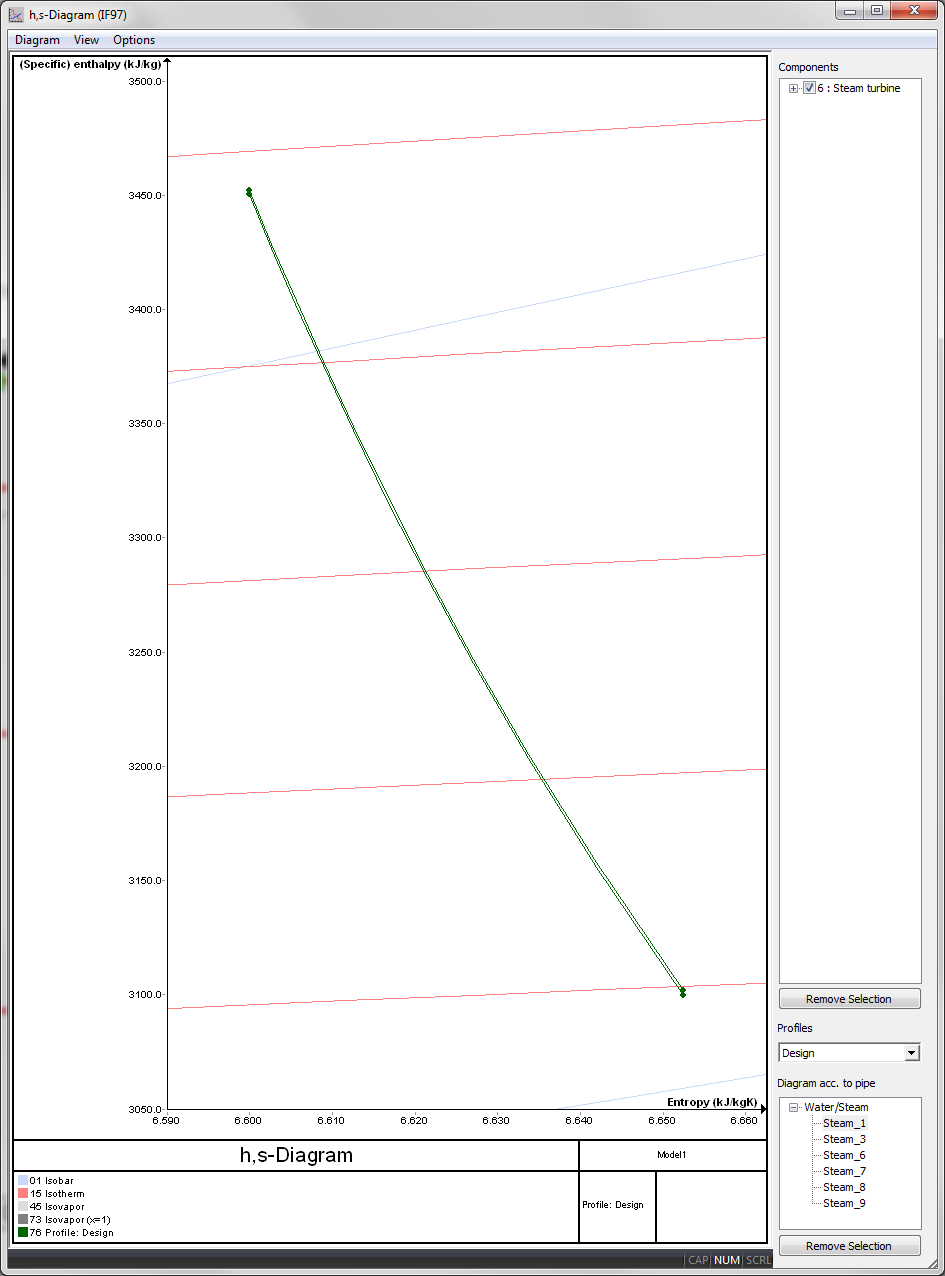
Abbildung 5: H-S-Diagramm mit Expansionslinien auf Basis statischer und totaler Zustandsgrößen in realistischen Proportionen.
Der Enthalpieabfall in diesem Beispiel beträgt im Fall der Verwendung statischer Zustandsgrößen 350.442 kJ/kg,, während er bei Verwendung totaler Zustandsgrößen 350.135 kJ/kg betragen würde, was einer Differenz von weniger als einem Zehntelprozent entspricht.
Nichtsdestotrotz bietet EBSILON dem Anwender die Option, den Effekt der kinetischen Energie mit der Spezifikation FSPEC als 'Spezialmodus mit Verwendung von totalem isentropen Wirkungsgrad und CKIN1 und CKIN2' (FSPEC = 1) zu berücksichtigen. Abbildung 6 zeigt das Ergebnis der Energiebilanz um Bauteil 6 unter Verwendung dieser Methode.
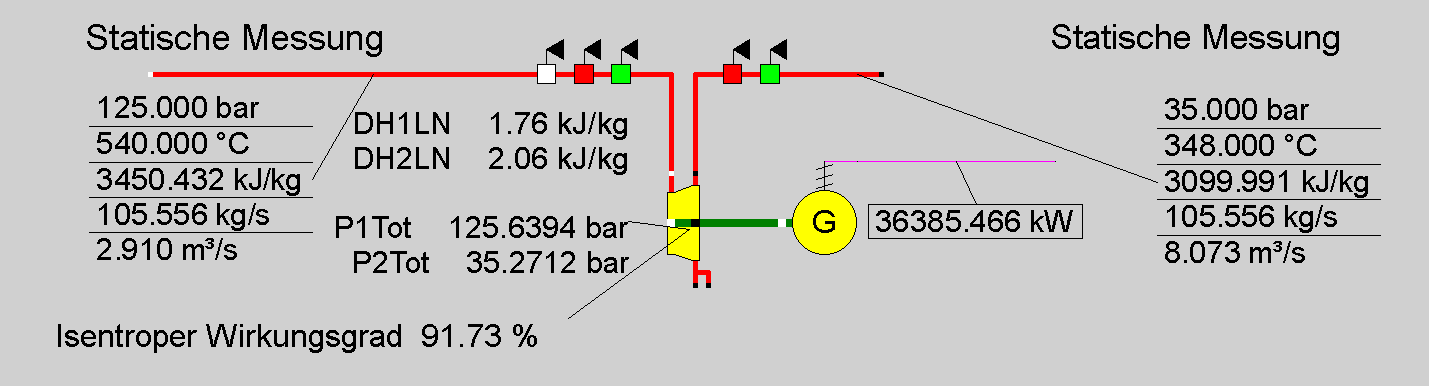
Abbildung 6: Energiebilanz um Bauteil 6 unter Verwendung statischer Zustandsgrößen und FSPEC = 1.
Besondere Sorgfalt muss angewendet werden, wenn Bauteil 6 zur Modellierung der letzten Turbinensektion vor einem Kondensator verwendet werden soll. In diesem Fall liegen die Dampfgeschwindigkeiten beim Austritt aus der Expansionsstufe in Bereich von 100 bis 260 m/s, und in Teillast in Sonderfällen sogar bei Schallgeschwindigkeit, die für Dampf ca. 410 m/s beträgt, mit entsprechender kinetischer Energie im Bereich von 5 bis 80 kJ/kg. In einem solchen Fall kann der kinematische Anteil der Enthalpie nicht mehr vernachlässigt werden, insbesondere, da diese Energie von der Turbine nicht zurückgewonnen werden kann. Sie muss deshalb als Austrittsverlust angesehen werden, der über den Kondensator an die Umgebung dissipiert werden muss.
Wenn ausreichende Information aus Messwerten zur Verfügung stünden, könnte ein Benutzer das Reverse-Engineering einer spezifischen Expansionsturbine ins Auge fassen. In diesem Fall wird die Verwendung des Bauteils 122 für die Modellierung des Kondensationsteils empfohlen. Bauteil 122 verwendet industrieübliche Methoden um die Expansionswirkungsgrade korrekt für die Expansion ins Nassgebiet zu korrigieren und Austritts- und Ventilationsverluste zu berücksichtigen. Zudem würde Bauteil 122 auch die Expansion in der letzten Stufe bei der Mach-Zahl gleich 1 begrenzen, was auch in der Realität ein physikalisches Limit für die Expansion in der letzten Stufe der Dampfturbine darstellt.
Polytroper Wirkungsgrad
Mit dem Schalter FETA kann zwischen isentropem (ETAIN) und polytropem (ETAPN) Wirkungsgrad umgeschaltet werden. Als Ergebniswert werden beide (ETAI und ETAP) ausgerechnet.
Die Umschaltung auf externen Vorgabe des Wirkungsgrades auf dem Logikanschluss 7 mit dem Schalter FVALETAI war nur bei Verwendung des isentropen Wirkungsgrades (FETA=0) möglich. Jetzt wird die externe Vorgabe auch auf den polytropen Wirkungsgrad (bei FETA=1) angewandt.
Da die Berechnung des polytropen Wirkungsgrades ETAP sehr zeitaufwändig ist (in manchen Fällen mit komplexen Stoffdaten vervielfacht sich dadurch die Gesamtrechenzeit des Modells), wird der Ergebniswert ETAP nicht mehr automatisch bei jeder Simulation berechnet. Wie schon beim Verdichter (Bauteil 24), wurde jetzt auch bei Bauteil 6 ein Schalter FOUTETAP eingeführt, mit dem man einstellen kann, ob ETAP berechnet werden soll oder nicht.
Logikeingang (Anschluss-Nr. 7) zur Steuerung von Komponenteneigenschaften
(siehe dazu auch Objekte bearbeiten --> Anschlüsse) )
Um Komponenteneigenschaften wie Wirkungsgrade oder Wärmeübergangskoeffizienten (Variationsgröße) von außen zugänglich zu machen (für Regelung oder Validierung), ist es möglich, den entsprechenden Wert als indizierten Messwert (Vorgabewert FIND) auf einer Hilfsleitung zu platzieren. Im Bauteil muss dann derselbe Index als Vorgabewert IPS eingetragen werden.
Es besteht auch die Möglichkeit, diesen Wert auf einer Logikleitung zu platzieren, die direkt an das Bauteil angeschlossen ist (siehe dazu FVALETAI=2, Variationsgröße: ETAIN, Dimension: Enthalpie). Der Vorteil besteht darin, dass die Zuordnung grafisch sichtbar ist und dadurch Fehler (zum Beispiel beim Kopieren) vermieden werden.
Die Aktivierung dieser Logikleitung kann auch vom Berechnungsmodus abhängig gemacht werden. Dadurch kann dieses Feature auch für Auslegungen verwendet, ohne dass ständig manuell umgeschaltet werden muss. Hierfür gibt es beim Schalter FVALETAI die Einstellungen
Diese Option steht für die Bauteile 2, 6, 8, 13, 18, 19, 23, 24 und 94 zur Verfügung.
Bei den Wärmetauschern sind diese Einstellmöglichkeiten unnötig, da die Nutzung der Logikleitung zur Vorgabe von KAN ohnehin nur in Offdesign-Rechnungen möglich ist. Im Design wird KAN ja von Ebsilon berechnet.
Wenn der Anschluss 7 nicht zur Wirkungsgradvorgabe verwendet wird, aber vorhanden ist, wird dort der Wirkungsgrad als Enthalpie ausgegeben. Abhängig von FETA wird der isentrope Wirkungsgrad ETAIN oder der polytrope Wirkungsgrad ETAPN ausgegeben.
|
FP1N |
Schalter für Art der Druckvorgabe
Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: P1=P1NSET (berechnet aus Stodola-Gesetz) |
|
P1NSET |
Eintrittsdruck (nominal) |
|
FIDENT |
Komponentenidentifikation =0: keine Identifikation |
|
FETA |
Art des Wirkungsgrades Ausdruck =0: Isentroper Wirkungsgrad |
|
FVALETAI |
Validierung des isentropen Wirkungsgrades Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: ETAIN / ETAPN verwendet (ohne Validierung) =2: ETAIN / ETAPN durch Enthalpie auf Regeleingang 7 gegeben =4: Enthalpie auf Regeleingang 7 verwendet in Design, Vorgabewert ETAIN / ETAPN im Off-Design verwendet =5: Vorgabewert ETAIN /ETAPN verwendet in Design, Enthalpie auf Regeleingang 7 im Off-Design verwendet |
|
ETAIN |
Isentroper Wirkungsgrad (nominal) |
|
ETAPN |
Polytroper Wirkungsgrad (nominal) |
|
IPS |
Index für Pseudomessstelle |
|
ETAMN |
Mechanischer Wirkungsgrad (nominal) |
|
QLOSSM |
Mechanischer Verlust (konstanter Anteil), auf 5% beschränkt (Warnmeldung, wenn QLOSSM>5%: "QLOSSM auf 5% beschränkt") |
|
DH1LN |
Kinetische Energie am Eintritt (nominal) |
|
DH2LN |
Enthalpieverlust am Austritt (nominal) |
|
FQ |
Veraltet: Schalter für den Leistungsfluss am Punkt 5 Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Leistung addieren zur Leistung der Welle auf der Hochdruckseite |
|
FSPECQ |
Schalter für Vorgabe von Leistung oder Massenstrom Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Massenstrom von außen gegeben, Leistung berechnet |
|
FSPEC |
Schalter für Typ der Wirkungsgradberechnung Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Ebsilon Standard, (CKIN1 und CKIN2 wird nicht verwendet), (VM1N wird verwendet), |
|
FCHR |
Schalter für Typ der Kennlinie Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: ETAI/ETAIN = f(M1/M1N) |
|
FMODE |
Schalter für Berechnungsmodus Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: GLOBAL |
|
FADAPT |
Schalter für Adaptionspolynom/Adaptionsfunktion Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: nicht verwendet und nicht ausgewertet |
|
EADAPT |
Anpassungsfunktion |
|
A2 |
Austrittsquerschnitt (wird nur zur Berechnung der Austrittsgeschwindigkeit verwendet, nicht für Austrittsverluste) |
| FOUTETAP | Ergebniswert ETAP nur dann berechnen, wenn dieser Wert 1 ist |
|
P2N |
Austrittsdruck (nominal) |
|
H1N |
Total Enthalpie am Eintritt (nominal) |
|
H2N |
Total Enthalpie am Austritt (nominal) |
|
T1N |
Eintrittstemperatur (nominal) |
|
M1N |
Eintrittsmassenstrom (nominal) |
|
VM1N |
Eintrittsvolumenstrom (nominal) |
|
VM2N |
Austrittsvolumenstrom (nominal) |
Die blau markierten Identifikationswerte sind Referenzwerte für den Teillastmodus. Diese Werte werden in den jeweiligen Gleichungen als Ist-Teillastwerte verwendet. Handelt es sich bei diesen Identifikationswerten um Strömungsdaten, stammen diese Werte oft von angeschlossenen Leitungen oder berechneten Werten.
Generell sind alle sichtbaren Eingaben erforderlich. Häufig werden jedoch Standardwerte zur Verfügung gestellt.
Für weitere Informationen über die Farbe der Eingabefelder und ihre Beschreibungen siehe Komponenten bearbeiten\Vorgabewerte
Für weitere Informationen über Auslegung vs. Teillast und Nominalwerte siehe Allgemeines\Nominalwerte übernehmen
Kennlinie 1 Wirkungsgradkennlinie
FCHR=0: ETAI/ETAIN = f(M1/M1N) =f(Wert)
FCHR=1: ETAI/ETAIN = f((P1/P2)/(P1N/P2N)) =f(Wert)
FCHR=2: ETAI/ETAIN = f (VM1/VM1N) =f(Wert)
|
Kennlinie 1: Wirkungsgrad |
|
X-Achse 1 Wert 1. Punkt
.
|
Kennlinie 2: Kinetische Anteile am Eintritt (Kennlinie nur im Modus "totaler isentroper Wirkungsgrad" relevant)
|
Kennlinie 2: kinetische Anteile am Eintritt |
|
X-Achse 1 VM1/VM1N 1. Punkt
.
|
Kennlinie 3: Kinetische Anteile am Austritt (Kennlinie nur im Modus "totaler isentroper Wirkungsgrad" relevant)
| Kennlinie 3: kinetische Anteile am Austritt |
|
X-Achse 1 VM2/VM2N 1. Punkt
. |
Kennlinie 4: Korrekturkennlinie für den Stodola-Druck
|
Kennlinie 4: Korrekturkennlinie für den Stodola-Druck |
|
X-Achse 1 M1/M1N 1. Punkt
.
|
Mit dieser Kennlinie wird ein Korrekturfaktor definiert, mit dem der nach dem Stodola'schen Dampfkegelgesetz ermittelte Druck multipliziert wird. Dies erleichtert eine Anpassung des Druckverlaufs an reale Anlagenzustände.
NennlastfallSimulationsschalter: GLOBAL = Nennlast und FMODE = GLOBAL wenn FP1N = "P1 von außen gegeben" |
||
|
P1 = P von außen (P Eintritt) (1) |
||
|
wenn FP1N = "P1N=P1NSET" |
||
|
P1 = P1NSET (1) |
||
|
|
||
TeillastfallSimulationsschalter: GLOBAL = Teillast oder FMODE = lokale Teillast wenn FP1N = "P1 von außen gegeben" |
||
|
P1 = P von außen (P Eintritt) (1) |
||
|
wenn FP1N = "P1N=P1NSET" |
||
|
entsprechend Einstellung P1 Berechnung gemäß Einstellung Ideales Gas oder Reales Gas ( Modelleinstellungen --> Simulation - Berechnung ) und entsprechend Gleichung nach Stodola Siehe dazu : Teillast Berechnung der Turbine
|
||
|
Alle Betriebsfälle |
||
|
X1 = f (P1,H1) S1 = f (P1,H1) V1 = f (P1,H1) VM1 = M1 * V1 S2S = S1 H2S = f (P2,S2S) DHS = H1 - H2S wenn GLOBAL= Nennlast und FMODE = GLOBAL, dann gilt ETAI = ETAIN sonst { wenn FCHR = 0 FAK = M1/M1N ETAI = ETAIN * f (FAK) aus Kennlinie wenn FCHR = 1 FAK = (P1/P2)/(P1N/P2N) ETAI = ETAIN * f (FAK) aus Kennlinie wenn FCHR = 2 FAK = VM1/VM1N ETAI = ETAIN * f (FAK) aus Kennlinie } Austrittsverluste wenn GLOBAL= Nennlast and FMODE = GLOBAL, dann DH2L = DH2LN sonst { FAK = VM2/VM2N DH2L = DH2LN*FAK*FAK } DH = DHS * ETAI H2 = H1 - DH + DH2L X2 = f (P2,H2) T2 = f (P2,H2) M1 = M2 + M3 + M4 P3 = P2 T3 = T2 H3 = H2 Q3 = M3 * H3 P4 = P2 T4 = T2 H4 = H2 Q4 = M4 * H4 M2 = M1 - M3 - M4 Q2 = M2 * H2 wenn FQ1 = 0, FAKT = 1 wenn FQ1 = 1, FAKT = -1 H6 = (M1*(H1-H2)*ETAM + M5*H5*FAKT)/M6 |
||
|
Totaler isentroper Wirkungsgrad |
||
Auslegunggegeben: P1statisch, H1total, (c1N)2/2P2statisch, ETAN, (c2N)2/2 mit: c1 = Geschwindigkeit am Eintritt c2 = Geschwindigkeit am Austritt (c1N)2/2 = DH1LN (c2N)2/2 = DH2LN H1statisch =H1total - (c1N)2/2 S1=f(P1statisch, H1statisch) P1total=f(H1total ,S1) H2isentropic_total=f(S1,P2total) xxx) Totaler isentroper Wirkungsgrad : ETAN = H1total - H2total_____ H1total - H2isentrop_total ETAN gegeben im Auslegungsfall H2total = H1total - ETAN* (H1total-H2isentrop_total) S2=f(P2statisch, H2total -(c2N)2/2) P2total=f(H2total,S2) Iteration: gehe zu xxx) |
||
Teillastgegeben: H1total, (c1N)2/2 - Kennlinie, M1 P2static, ht - Kennlinie, (c2N)2/2 - Kennlinie P1total=f(Stodola-Gleichung) xx) V1total=f(P1total,H1total) Iteration: gehe zu xx) S1=f(P1total,H1total) H2isentrop_total =f(S1,P2total) xxx) ht aus Kennlinie H2total = H1total - ht* (H1total-H2isentrop_total) H2statisch =H2total -(c2N)2/2 S2=f(P2static, H2static) P2total=f(H2total,S2) Iteration: gehe zu xxx) H1statisch =H1total -(c1N)2/2 P1statisch=f(S1, H1statisch) |
||
Identifikationsmodus: Für FCHR = -1 oder FCHR = -2 wird der Wirkungsgrad rückwärts berechnet. Wenn zum Beispiel die Leistung gegeben ist (Enthalpie), wird der ETAI berechnet. In diesem Fall werden ETAIN und die angegebenen Kennlinien ignoriert.
|
Isentroper Wirkungsgrad |
ETAI | - |
| Polytroper Wirkungsgrad | ETAP | - |
| Mechanischer Wirkungsgrad (einschließlich QLOSSM) | ETAM | - |
| Eintritts-Dampfgehalt | X1 | - |
| Austritts -Dampfgehalt | X2 | - |
| Kinetische Energie am Eintritt | DH1L | kJ/kg |
| Austrittsverlust | DH2L | kJ/kg |
| Totaler Druck am Eintritt | P1T | bar |
| Totaler Druck am Austritt | P2T | bar |
| Entropie am Eintritt | S1 | kJ/kgK |
| Entropie am Austritt | S2 | kJ/kgK |
| Eintritts-Volumenstrom | VM1 | m3/s |
| Austritts-Volumenstrom | VM2 | m3/s |
| Austrittsgeschwindigkeit | WAX | m/s |
| Bezogener Massenstrom | M1M1N | - |
| Bezogenes Druckverhältnis | P1P2N | - |
| Bezogener Volumenstrom | VM1VM1N | - |
| Verwendeter Wert für nominalen isentropen Wirkungsgrad | ETAINR | - |
| Verwendeter Wert für nominalen polytropen Wirkungsgrad | ETAPNR | - |
| Bezogener Wirkungsgrad | ETAETAN | - |
| Wirkungsgrad gemäß Kennlinie | ETACL | - |
| Ergebnis für ADAPT / EADAPT | RADAPT | - |
| Für FSPEC=0; fiktives P1N für Anpassungsrechnung | P1NST | bar |
| Erzeugte Wellenleistung | QSHAFT | kW |
| Veraltet: Erzeugte mechanische Leistung nur aus 5 und 6 | DQ65 | kW |
 |
Form 1 |
 |
Form 2 |
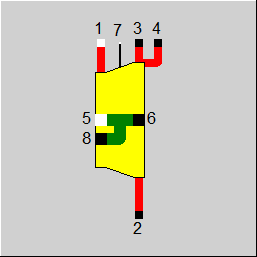 |
Form 3 |
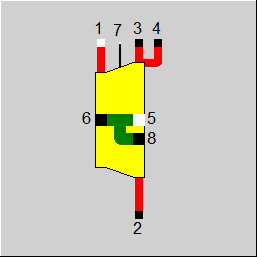 |
Form 4 |
Klicken Sie hier >> Bauteil 6 Demo << um ein Beispiel zu laden.