EBSILON®Professional Online Dokumentation
Es sind bei der Minimierung der Fehlerquadratsumme zusätzlich zu den physikalischen Gleichungsnebenbedingungen auch Ungleichungen zu berücksichtigen. Diese ergeben sich z.B. aus der Forderung, dass Wirkungsgrade oder Dampfgehalte kleiner 1 sein sollen.
Solche Ungleichungsnebenbedingungen können in das Iterationsschema Glg. (18) für das durch Glg. (1,2) definierte Minimalwertproblem integriert werden.
Dazu beobachten wir, dass, wenn die Ungleichung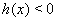 
gilt, ein 
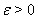exisitiert, so dass 
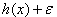= 0 ist. Durch Einführen einer Schlupfvariable y als Hilfsvariable können Ungleichungen damit im Rahmen unseres Formalismus durch zusätzliche Gleichungsnebenbedingungen 
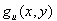im Rahmen der Hilfsgrößendefinitionsgleichungen abgebildet werden:
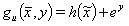(27)
oder
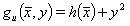(28)
Die Terme y² bzw. ey sind immer positiv, sodass die Gleichungsnebenbedingungen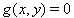 
nur erfüllt werden können, wenn die Ungleichungsbedingungen für 
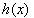eingehalten werden.
Glg. (27) erzwingt wegen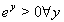 
, streng 
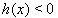, während Glg. (28) für y=0 auch h(x) = 0, also Lösungen genau auf dem Rand zulässt.
Der Iterationsformalismus nimmt die Invertierbarkeit der Hilfsgrößendefinitionsgleichungen an. Wegen
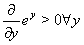fügt sich Glg. (27) nahtlos in den beschriebenen Formalismus ein. Glg. (27) entspricht dabei der Glg. (39) in VDI 2048, Blatt 2. Die Einführung von Fangbereichen zum Ein-/Ausschalten der Nebenbedingungen ist bei einer Formulierung des Iterationsverfahrens gemäß Glg. (18) nicht erforderlich.
Nebenbedingungen vom Typ der Glg. (28) verletzen die Invertierbarkeit (nur) am Rand, können aber durch Fallunterscheidungen im Algorithmus berücksichtigt werden. Z.B. sucht man zunächst mit der Einschränkung y >0 Minima innerhalb des zulässigen Bereichs und in zweiten Schritt mit der Nebenbedingung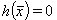 
statt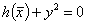 
Minima auf dem Rand. Das kleinste ist die gewünschte Lösung.