Die mathematische Formulierung der Aufgabenstellung

---

Die VDI 2048 führt eine Gaußsche Ausgleichsrechnung durch. Dazu wird zu einem Satz von Rohdaten 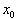ein verbesserter Datensatz von Schätzwerten 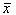so bestimmt, dass die mit der empirischen Kovarianzmatrix 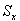berechneten Fehlerquadratsumme minimal wird; 

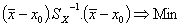           (1)

Dabei sind 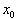, 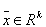. Bei der Minimierung sind die physikalischen Gesetze, denen die Messwerte genügen müssen, als Nebenbedingungen einzuhalten. Diese Nebenbedingungen sollen hier in der Form

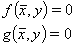                                      (2)

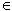
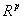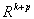
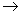
formuliert werden. Dabei ist y ein Vektor von Hilfsvariablen, die p Gleichungen g: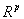sind die Definitionsgleichungen der Hilfsvariablen und die Gleichungen f: 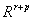0 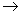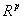sind die r physikalischen Nebenbedingungen, die unter Zuhilfenahme der p Hilfsvariablen definiert worden sind.

Da die Gleichungen g die Definitionsgleichungen der Hilfsvariablen sein sollen, nehmen wir an, dass die Gleichungen 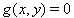 nach y aufgelöst werden können, d.h. dass die p x p Funktionalmatrix

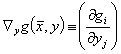
in einer  Umgebung der Lösung (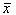,y) von g(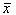,y)=0 invertierbar ist.

Die Hilfsvariablen gehen nicht direkt in die Berechnung der Fehlerquadratsumme Glg. (1) ein. Sie sind durch die Hilfsgrößendefinitionsgleichungen bestimmt. Dem entsprechend werden für die Hilfsgrößen auch keine empirischen Kovarianzen angegeben, sondern Kovarianzen, wie in der VDI 2048 beschrieben, im Rahmen einer Fehlerfortpflanzung aus den empirischen Kovarianzen der Rohdaten bzw. der Schätzwerte berechnet.