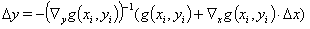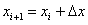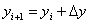Zur Ableitung eines Iterationsverfahrens werden die Gleichungen (4 - 7) linearisiert. Wegen der bilinearen Struktur der Fehlerquadratsumme und der vorausgesetzten Invertierbarkeit der Funktionalmatrix der Definitionsgleichungen der Hilfsvariablen 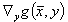 , ist können die Lagrangemultiplikatoren aus den entstehenden Gleichungen eliminiert werden. Die Iteration erfolgt daher nur in den Verbesserungen der Schätzwerte und in den Hilfsgrößen. Dies entspricht wiederum dem in der VDI 2048 vorgeschlagenen Verfahren.
, ist können die Lagrangemultiplikatoren aus den entstehenden Gleichungen eliminiert werden. Die Iteration erfolgt daher nur in den Verbesserungen der Schätzwerte und in den Hilfsgrößen. Dies entspricht wiederum dem in der VDI 2048 vorgeschlagenen Verfahren.
Es handelt sich hierbei letztendlich um eine Variante des klassischen Newtonverfahrens zur numerischen Minimierung unter Nebenbedingungen.
Für die Linearisierung der Glgn. (4 -7) sei angesetzt 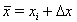 ,
, 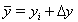 worin
worin 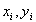 die Werte im i-ten Iterationsschritt sind. Dann ergibt sich in niedrigster Ordnung:
die Werte im i-ten Iterationsschritt sind. Dann ergibt sich in niedrigster Ordnung:
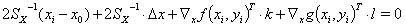 (4a)
(4a)
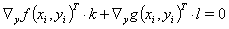 (5a)
(5a)
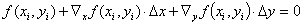 (6a)
(6a)
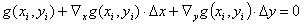 (7a)
(7a)
Wegen der Invertierbarkeit der Definitionsgleichungen der Hilfsvariablen erhalten wir aus Glg. (5a) einen Zusammenhang zwischen den Lagrangemultiplikatoren
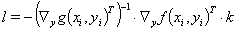 (8)
(8)
Das Ergebnis (8) können wir in Glg. (4a) einsetzen. Damit ergibt sich
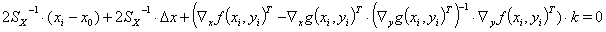 (9)
(9)
oder wegen 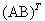 =
= 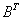
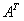 ,
, 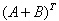 =
= 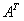 +
+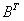 ,
, 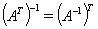
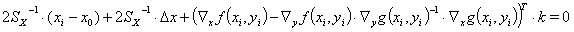 (9a)
(9a)
Zur Vereinfachung der Schreibweise sei an dieser Stelle eine transformierte Funktionalmatrix 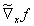 definiert durch
definiert durch
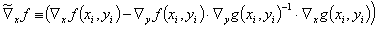 (10)
(10)
Dann wird aus Glg. (9a)
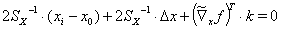 (11)
(11)
Es sei darauf hingewiesen, dass für den ersten Iterationsschritt mit 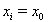 , Glg. (10) der Glg. (115) in der VDI 2048, Bl .1 mit einer zur Eliminierung der Hilfsvariablen transformierten Funktionalmatrix entspricht.
, Glg. (10) der Glg. (115) in der VDI 2048, Bl .1 mit einer zur Eliminierung der Hilfsvariablen transformierten Funktionalmatrix entspricht.
Aus der Glg. (7a) kann wieder wegen der Invertierbarkeit der Definitionsgleichungen der Hilfsvariablen die Verbesserung der Hilfsvariablen aus der Verbesserung der Messwerte bestimmt werden:
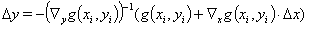 (12)
(12)
Einsetzen von Glg. (12) in Glg. (6a) ergibt
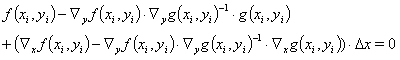 (12a)
(12a)
Mit der bereits eingeführten transformierten Funktionalmatrix 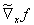 und einem entsprechend definierten transformierten Vektor der Widersprüche
und einem entsprechend definierten transformierten Vektor der Widersprüche
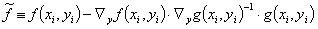 (13)
(13)
wird aus Glg. 12a
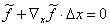 (14)
(14)
Glg. (14) entspricht Glg. (112) in der VDI 2048 Bl. 1 nach einer Transformation zur Eliminierung der Hilfsvariablen. Aus den Glgn (11) und (14) kann man, wie in der Richtlinie vorgeführt, die Lagrangemultiplikatoren k eliminieren, um die Verbesserungen Dx zu bestimmen
Glg. (11) ergibt
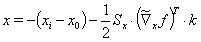 (15)
(15)
Durch Einsetzen von Glg. (15) in Glg. (14) bestimmen sich die Lagrangemultiplikatoren k
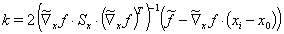 (16)
(16)
Glg. (16) kann wieder in Glg. (15) verwendet werden, um letztendlich die Verbesserungen Dx zu bestimmen:
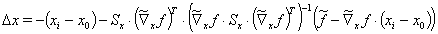 (17)
(17)
Das ist im ersten Iterationsschritt mit 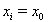 , genau die in VDI 2048 Bl. 1 in Glg. (120) angegebene Verbesserung. Ohne die in Glg. (17) für
, genau die in VDI 2048 Bl. 1 in Glg. (120) angegebene Verbesserung. Ohne die in Glg. (17) für 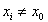 , zusätzlich auftretenden Terme führt das hier beschriebene Iterationsverfahren zwar zu einer Lösung, die die Nebenbedingungen erfüllt, aber nicht notwendig zu dem Minimum der Fehlerquadratsumme. Dies ist in Anhang 6.3 an einem einfachen Beispiel gezeigt. Die zusätzlichen Terme stellen die Konvergenz in ein (lokales) Minimum der Fehlerquadratsumme sicher.
, zusätzlich auftretenden Terme führt das hier beschriebene Iterationsverfahren zwar zu einer Lösung, die die Nebenbedingungen erfüllt, aber nicht notwendig zu dem Minimum der Fehlerquadratsumme. Dies ist in Anhang 6.3 an einem einfachen Beispiel gezeigt. Die zusätzlichen Terme stellen die Konvergenz in ein (lokales) Minimum der Fehlerquadratsumme sicher.
Zusammenfassend ist damit das in EBSILON implementierte Iterationsverfahren nach VDI 2048 zur Minimierung der Fehlerquadratsumme unter Nebenbedingungen und unter Berücksichtigung von Hilfsvariablen gegeben durch die Glgn. (10, 13, 17, 12):
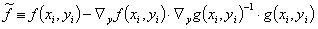
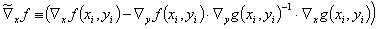
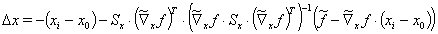 (18)
(18)