

Für die Verteilungsfunktion einer Zufallsvariablen x muss gelten:
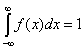 (1)
(1)
Der Erwartungswert von x ist definiert als
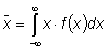 (2)
(2)
und die Varianz als
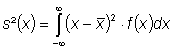 (3)
(3)
Die Standardabweichung ergibt sich aus der Quadratwurzel
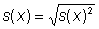 (4)
(4)
Sind die Wahrscheinlichkeitsdichten nicht bekannt, so können erwartungstreue Schätzwerte für Mittelwert und Varianz aus Stichproben gewonnen werden.
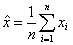 (5)
(5)
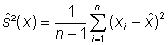 (6)
(6)
Stochastische Unabhängigkeit zwischen zwei Zufallsvariablen x und y besteht, wenn
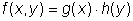 (7)
(7)
gilt.
D.h. die Wahrscheinlichkeitsdichte x und y gemeinsam anzutreffen, ist gleich dem Produkt der einzelnen Wahrscheinlichkeitsdichten. Unter der Kovarianz versteht man
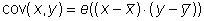 (8)
(8)
Der Operator e stellt die Erwartungswertbildung im Sinne von Gl. (2) dar. Die Kovarianz ist ein Maß für die gegenseitige Abhängigkeit von x und y. Eine abgeleitete Größe ist der Korrelationskoeffizient
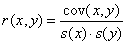 (9)
(9)
Es lässt sich zeigen, dass stets gilt:
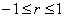 (10)
(10)
Für einen linearen Zusammenhang
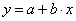 (11)
(11)
gilt:
wenn b positiv: r(x,y) = 1
wenn b negativ ist : r(x,y) = -1
Sind die Variablen voneinander unabhängig, so ist
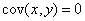
Bei vielen Zufallsvariablen empfiehlt sich die Matrixschreibweise:
Variablenvektor Transponierter Variablenvektor
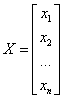
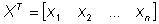 (12)
(12)
Kovarianzmatrix:
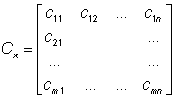 (13)
(13)
Die Diagonalelemente sind die Varianzen
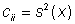 (14)
(14)
Ferner gilt Symmetrie
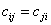 (15)
(15)
Bezeichnet man mit E den Operator für die Erwartungswertbildung, so lässt sich schreiben:
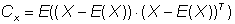 (16)
(16)
Das Fehlerfortpflanzungsgesetz geht aus folgender Betrachtung hervor. Der Vektor Y ergibt sich aus X durch die Lineartransformation
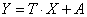 (17)
(17)
Für Erwartungswert und Kovarianz von Y gilt:
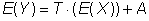 (18)
(18)
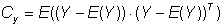 (19)
(19)
Mit (17) und (18) folgt:
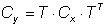 (20)
(20)
Unter der Annahme, dass sich die yi in der Umgebung der Erwartungswerte E(X) linear darstellen lassen, ergibt sich
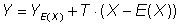 (21)
(21)
mit
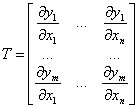 (22)
(22)
Wird Gl. (22) in Gl. (20) eingesetzt, so gelangt man zum Fehlerfortpflanzungsgesetz. Sind die x voneinander unabhängig, so enthält Cx nur die Diagonalelemente, und für die Varianzen der yi ergibt sich
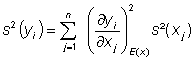 (23)
(23)
Verteilung des Schätzwerts der Varianz bei normalverteilter Grundgesamtheit:
Die Variable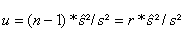 (24)
(24)
folgt einer Chi2-Verteilung des Freiheitsgrads r mit dem Erwartungswert
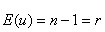 (25)
(25)
und der Varianz
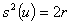 (26)
(26)
Die Variable
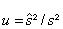 (27)
(27)
folgt einer speziellen F-Verteilung (Fisher-Verteilung mit zwei Parametern: Freiheitsgrad r und unendlich) mit dem Erwartungswert
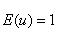 (28)
(28)
und der Varianz
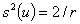 (29)
(29)
Bezieht man die ermittelte bezogene Fehlerquadratsumme auf die 95 %-Quantile der Verteilungsfunktion, so erhält man ein Bewertungskriterium für die Anpassungsgüte, das als Chi2-Testverhältnis bezeichnet werden kann.
Chi2-Testverhältnis <= 1 Anpassung vertrauenswürdig
> 1 zu große Widersprüche in den Messdaten