

Durch Einsetzen von Rohdaten in die Bilanzgleichungen (Nebenbedingungen) lassen sich grobe Fehler der Messwerte oder der Modellierung erkennen. Es werden Widersprüche aufgedeckt. Dazu ist notwendig, dass die strenge Einhaltung der Bilanzgleichungen aufgehoben wird. Es wird dabei die Korrektheit der Messwerte unterstellt, und die Verletzungen der Bilanzgleichungen einschließlich deren Vertrauensintervalle berechnet.
Dazu ist unter Extras à Modelleinstellungen unter Validierung die Validierungsmethode "Rohdatenanalyse" auszuwählen.
Es werden für alle Bilanzgleichungen die Abweichungen berechnet, aber für eine Liste nur solche ausgewählt, bei denen die bezogene Abweichung die im Feld "Grenze für die Anzeige grober Verletzungen" angegebenen Wert überschreitet. Standardmäßig wird dieser Wert auf 1 gesetzt, was bedeutet, dass die festgestellte Abweichung ihr zugehöriges Konfidenzintervall übersteigt. In diesem Fall spricht man von einer groben Verletzung.
An einem sehr einfachen Beispiel soll der Sachverhalt verdeutlicht werden.
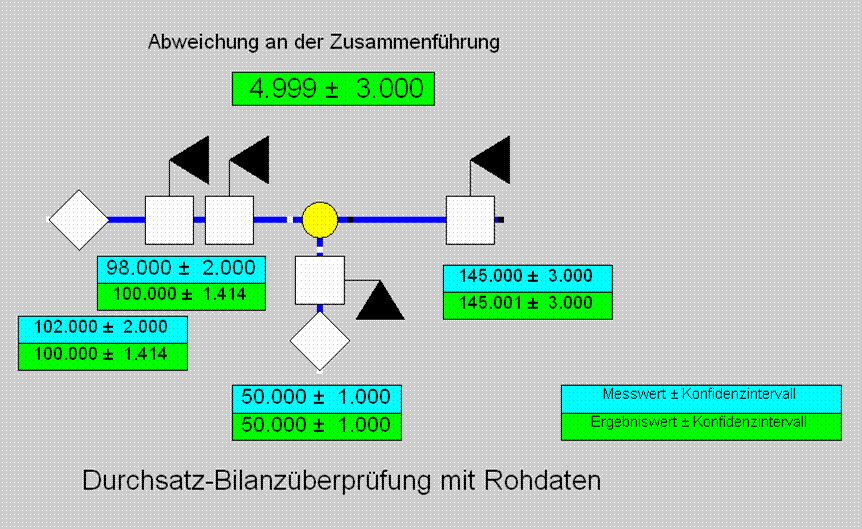
Diese Schaltung stellt eine einfache Zusammenführung da. Auf einer Zuleitung gibt es zwei Massenstrom-Messungen. Für die Rohdatenanalyse muss man in diesem Fall die Leitung aufschneiden und einen Trenner einbauen, den man aber auf FSPEC="nichts" einstellt, so dass er im Simulationsmodus nicht als Trenner wirkt, sondern alle Größen am Austritt gleich denen am Eintritt setzt.
Wenn man sich auf die Massenströme beschränkt, gibt es in dieser Schaltung zwei Bilanzgleichungen, nämlich die Massenbilanz der Zusammenführung M1+M3-M2=0 und die des Trenners M2-M1=0.
Nach der Rohdatenanalyse erhält man in der Gleichungsliste folgendes Ergebnis:
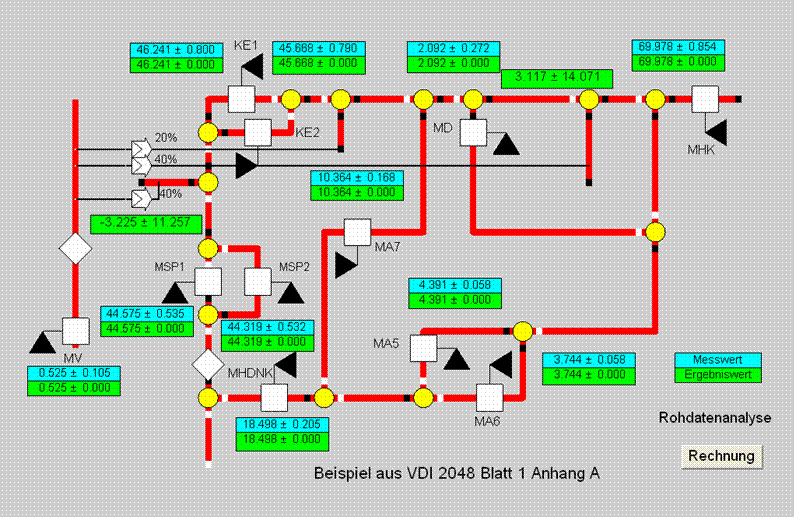
Das bedeutet, dass nur beim Trenner eine grobe Verletzung vorliegt. Die Verletzung an der Zusammenführung ist dagegen nicht als "grob" anzusehen.
Senkt man die Schwelle für die Anzeige auf 0.5, wird auch diese Gleichung angezeigt:
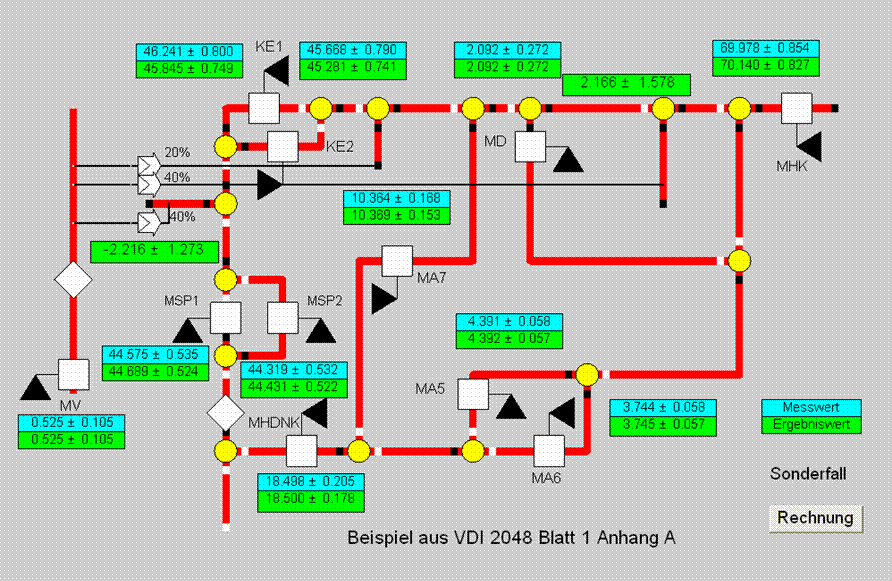
Man erkennt, dass diese Gleichung nicht grob verletzt ist, weil das Konfidenzintervall von 3.7417 größer als die Abweichung von 3.0 ist, d.h. die Abweichung liegt mit einer Wahrscheinlichkeit von 95 % innerhalb des Intervalls von -0.7417 und +6.7417. Der Wert "0" liegt also noch innerhalb des Konfidenzintervalls, d.h. es ist nicht zu 95 % sicher, dass eine Verletzung vorliegt.
Die Vorgehensweise soll nun am Beispiel der Schaltung eines Kernkraftwerks erläutert werden. Bei der ersten Durchrechnung eines Kraftwerkmodells mit näherungsweise festgelegten Spezifikationsdaten für die Aggregate erhält man in der Rohdatenanalyse folgendes Ergebnisbild mit zugehöriger Liste grober Verletzungen:
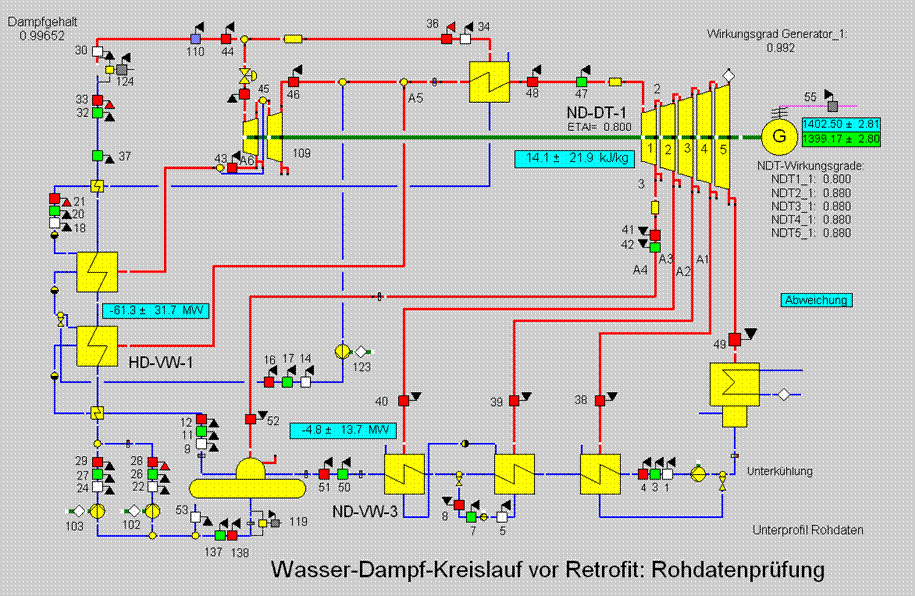
Durch Doppelklick auf die Spaltenüberschrift wurde die Liste nach der Größe der Abweichungen sortiert.
Als erstes fällt die große Verletzung an der Komponente "Heat_extraction_2" auf. Mit Hilfe des Fernglas-Buttons kann diese Komponente in der Schaltung gesucht werden. Es stellt sich heraus, dass es sich hier um die Stelle im Kreislauf handelt, an der die Wärme aus dem Primärkreis in den hier modellierten Sekundärkreis eingekoppelt wird. Die gemessene Wärmeeinkopplung ist in diesem Fall offensichtlich um 4.6 MW kleiner als sich aus den Messdaten des Sekundärkreises ergibt. Es muss nun überlegt werden, ob ein Modellierungsfehler vorliegt (z. B. Nebenleitungen nicht im Modell berücksichtigt, die für die Unstimmigkeiten verantwortlich sein könnten) oder ob tatsächlich die Messwerte entsprechend unplausibel sind.
Als nächstes würde man sich dann die Modellierung der Turbine "NDT2_1" vornehmen, danach untersuchen, was an der "Zusammenführung_5" passiert. Auf diese Weise hilft die Rohdatenanalyse bei der Korrektur des Modells.
Erst wenn die Modellierungsfehler so weit wie möglich beseitigt sind, lohnt es sich, mit der Validierungsrechnung fortzufahren.
Ergibt sich aus einer Validierungsrechnung ein Chi^2-Testverhältnis (bezogene Fehlerquadratsumme geteilt durch den Wert der Fisher-Verteilung) von größer als 1, was einer Verletzung der 95%-Quantile der F-Verteilung gemäß Bedingung 140 der Richtlinie VDI 2048 Blatt 1 entspricht oder weisen Messwerte zu große bezogene Abweichungen gemäß Gl. 141 VDI 2048 Blatt 1 aus, so sind entweder die Konfidenzintervalle nicht angemessen gesetzt worden oder es liegen Modellfehler vor. Kann letzteres ausgeschlossen werden, so erfolgt die Analyse gemäß Gl. 140 und 141 VDI 2048 Blatt 1 unter Beachtung von Korrelationen gemäß Gl.129 VDI 2048 Blatt 1 und entsprechend der Anleitung zur Fehleranalyse im Blatt 2 der Richtlinie Abschnitt 7.7.2.
Die Messwerte, die die größten Abweichungen nach Gl. 141 aufweisen, und diejenigen Messwerte mit einer erheblichen Korrelation zu ihnen müssen hinsichtlich ihrer Konfidenzintervalle eine verbesserte Einschätzung erfahren. Dieser Vorgang muss vom Benutzer unter Einbringen seines Wissens über die Anlage selbst durchgeführt werden und muss iterativ solange wiederholt werden, bis das Chi^2-Testverhältnis 1 oder besser erreicht. Hier liegt auch der Anknüpfungspunkt für eine zustandsorientierte Wartung des Messwesens. Über ein EbsScript-Programm kann eine Liste der Messwerte mit zu großen relativen Abweichungen zwischen validiertem Wert und Messwert generiert werden. Ebenso kann die Excel-Validierungsliste (siehe Retrofit-Beispiel) verwendet werden.
Mit Hilfe eines EbsScripts kann man sich die Arbeit erleichtern, indem man die Verbreiterung zunächst auf einzelne Messwerte (besonders große Ausreißer) anwendet und prüft, ob sich dadurch nicht schon andere automatisch in einen gültigen Bereich verschieben. Wenn ein hinreichend kleines Chi^2-Testverhältnis (bezogene Fehlerquadratsumme geteilt durch den Wert der Fisher-Verteilung) erreicht wurde, kann man untersuchen, ob gewisse Konfidenzintervalle von Messwerten zu breit angegeben wurden. Dafür kommen allerdings nur Messwerte in Frage, deren bezogene Abweichung gemäß Gl. 141 VDI 2048 Blatt 1 klein genug ist. Sie können nach sachgerechter Einschätzung enger gefasst werden, sofern sich das Chi^2-Testverhältnis nicht gravierend ändert und innerhalb der Grenzbedingung bleibt. Diese Untersuchung wird mit einem EbsScript-Programm systematisch durchgeführt und ergibt eine Vorschlagsliste für engere Konfidenzintervalle. Nach einer Prüfung, welche ursprünglichen Konfidenzintervalle zu breit angelegt waren, können Änderungen vorgenommen werden.