

|
Leitungsanschlüsse |
|
|
|
1 |
Logik- Eingang zur DNI-Vorgabe (als H) |
|
|
2 |
Logik-Ausgang für verwendetes DNI (als M), Einfallswinkel (als P) Sonnenhöhe (als H) und Azimut (als NCV) |
|
Allgemeines Vorgabewerte Verwendete Physik Bauteilform Beispiel
Dieses Bauteil bietet Methoden für die Berechnung von Sonnenstand und Einfallswinkeln auf Oberflächen für einachsige Nachführung. Der Nutzer ist gänzlich flexibel, ob er diese Werte aus geographischen Daten und der Zeit berechnen oder die Winkel direkt durch Vorgabewerte festlegen will. Alle Bauteile, die sich auf das Sonnenbauteil mit dem Index ISUN beziehen, können auf diese Daten zugreifen, müssen es aber nicht. Deshalb ist es möglich, Strahlungsdaten, die für mehrere Bauteile relevant sind, in einem einzelnen Bauteil zu ändern. Andererseits bietet jedes Bauteil die Funktionsweise, die Werte durch individuelle Werte außer Kraft zu setzen. Zusammen mit der Sonneneinstrahlung können die betreffenden Bauteile mit Umgebungsdaten versorgt werden.
Obwohl die Berechnung von Einfallswinkeln von der Ausrichtung jedes einzelnen Elements für die einachsige Nachführung abhängt und deshalb Teil des Berechnungsablaufs dieses Bauteils sein sollte, wird dem Nutzer die Möglichkeit geboten, diese Berechnung bereits im Sonnenbauteil einmalig für alle linienfokussierenden Bauteile durchzuführen.
Dieses Bauteil verfügt über zwei optionale Logikanschlüsse:
Die Ausgabe dieser Größen auf einem Logikausgang ermöglicht die Nutzung in logischen Konstruktionen. Damit können während der Iteration diese Größen zum Beispiel in Reglern und Schwellwertschaltern genutzt werden.
Hinweis: in Release 11 wurde DNI als Massenstrom und Sonnenhöhe als Enthalpie ausgegeben, d.h. es gab eine unterschiedliche Behandlung des DNI auf Eingangs- und Ausgangsleitung.
Im Zusammenhang mit dem neuen Messstellentyp FTYP=56 für DNI wurde dies bereinigt. Um zu vermeiden, dass sich dadurch Änderungen in logischen Konstruktionen und Regelungen ergeben, wurde ein Kompatibilitätsflag FCOMP eingeführt, das beim Erstellen einer neuen Schaltung den Wert 0 hat, beim Laden einer unter Release 11 (oder älter) erstellten Schaltung jedoch den Wert 11 bekommt.
Für FCOMP=11 wird weiterhin DNI als Massenstrom und die Sonnenhöhe als Enthalpie ausgegeben. Eine Messstelle mit FTYP=56 kann dann allerdings nicht verwendet werden.
Bei Vorgabe des DNI über eine logische Leitung wird im Auslegungsfall der Leitungsergebniswert auf den Vorgabewert DNI übernommen.
Das Bauteil 117 enthält die Kennlinie CHORIZON und den Schalter FHORIZON. Damit kann die Silhouette des Horizonts abgebildet werden, d. h. in welcher Richtung Berge, Bäume oder Häuser bis zu welcher Höhe (in Grad) die Sonne verdecken. Bei
Aus Gründen der Kompatibilität wird der damit errechnete Horizontwinkel nur zur Verfügung gestellt. Es obliegt den Solarbauteilen, diesen Wert auch zu verwenden.
|
FTFRAME |
Zeitreferenzsystem |
|
FTZONE |
Zeitzone basierend auf der UTC Definition, in der die Ortszeit gegeben wird (in Stunden östlich von Greenwich). Das ist definiert als der Längengrad des Zeitzonenmeridians. (siehe Auswahlbox Spezifikationswert) = 12... = 0... ... =-12... |
|
FSANGLE |
Methode zur Berechnung des Sonnenstands (Höhe und Azimutwinkel) =0: Keine Berechnung, benutze Parameter SHEIGHT und SAZIM |
|
FIANGLE |
Methode zur Berechnung des Longitudinal- und Transversal-Einfallswinkels (aus Sonnenposition und Kollektorausrichtung) =0: Berechnung aus Sonnenwinkeln |
|
LATI |
Breitengrad des Standorts (positiv auf der Nordhalbkugel, -90° bis 90°) |
|
LONG |
Längengrad des Standorts (positiv östlich von Greenwich / -180° bis 180°) |
|
DATETIME |
Datum und Zeit im Zeitrahmen, der durch FTFRAME gegeben wird |
|
SHEIGHT |
Sonnenhöhe (Winkel zwischen Sonnenmittelpunkt und Horizont) |
|
SAZIM |
Sonnenazimutwinkel (0° genau nördlich, positiv in östliche Richtung) |
|
CAZIM |
Kollektorazimutwinkel: Richtung der positiven Kollektorachse (Projektion auf horizontale Ebene, 0° ist genau nördlich, positiv in östliche Richtung). Die Richtung (positiv oder negativ) ist wichtig für die Bestimmung des Nachführungswinkels. |
|
CSLOP |
Kollektorneigung, Winkel zwischen Kollektorachse und horizontaler Ebene |
|
PHIINC |
Einfallswinkel (Rinne), (Winkel zwischen Sonnenstrahl und der Normalen einer einachsig nachgeführten Oberfläche) |
|
PHITRAN |
Nachführungswinkel einer Oberfläche für einachsige Nachführung. Ein Winkel von 0° bedeutet, dass die Oberflächennormale vertikal nach oben ausgerichtet ist. Der Winkel wird positiv, wenn die Normale im Uhrzeigersinn rotiert, wenn man in Richtung der positiven Kollektorachse blickt. Ein Umschalten der Achsenrichtung bedeutet eine Änderung im Vorzeichen des Nachführungswinkels. |
|
FDNI |
Definition direkter Strahlung =0: Vorgabewert DNI |
|
DNI |
Direkt-Normal-Strahlung. Dieser Wert wird allen Bauteilen zur Verfügung gestellt, die sich auf die Solarparameter ISUN beziehen. |
|
GHB |
Globale horizontale direkte Strahlung. Dieser Wert wird allen Bauteilen zur Verfügung gestellt, die sich auf die Solarparameter ISUN beziehen. |
|
GHD |
Globale horizontale diffuse Strahlung. Dieser Wert wird allen Bauteilen zur Verfügung gestellt, die sich auf die Solarparameter ISUN beziehen. |
|
ALTITUDE |
Höhe über dem Meeresspiegel. |
|
KT |
Klarheitsindex kT. Verhältnis zwischen der totalen Himmelsstrahlung zur Weltraumstrahlung bezogen auf eine eben Fläche. |
| FHORIZON | Horizont-Berechnungen |
|
TAMB |
Umgebungstemperatur. Dieser Wert wird allen Bauteilen zur Verfügung gestellt, die sich auf die Solarparameter ISUN beziehen. |
|
VWIND |
Windgeschwindigkeit. Dieser Wert wird allen Bauteilen zur Verfügung gestellt, die sich auf die Solarparameter ISUN beziehen. |
|
AWIND |
Windrichtung. Von Süden nach Norden 0°, positiv in östliche Richtung. Dieser Wert wird allen Bauteilen zur Verfügung gestellt, die sich auf die Solarparameter ISUN beziehen. |
|
ISUN |
Index des Sonnenbauteils, dessen Daten für die Berechnng genutzt werden |
|
FCOMP |
Kompatibilitätsmodus für Logikanschlüsse =0: DNI als H auf Anschluss 1 und 2, Höhe als M auf Anschluss 2 |
Generell sind alle sichtbaren Eingaben erforderlich. Häufig werden jedoch Standardwerte zur Verfügung gestellt.
Für weitere Informationen über die Farbe der Eingabefelder und ihre Beschreibungen siehe Komponenten bearbeiten\Vorgabewerte
Für weitere Informationen über Auslegung vs. Teillast und Nominalwerte siehe Allgemeines\Nominalwerte übernehmen
| Kennlinie 1 Name: CHORIZON Titel: Höhenwinkel des Horizonts als Funktion des Azimutwinkels Beschreibung: Damit kann die Silhouette des Horizonts abgebildet werden, d. h. in welcher Richtung Berge, Bäume oder Häuser bis zu welcher Höhe (in Grad) die Sonne verdecken. |
|
Horizont-Höhenwinkel = f (Azimutwinkel) |
|
RSHEIGHT |
Sonnenhöhe ((Winkel zwischen Sonnenmittelpunkt und Horizont) |
|
RSAZIM |
Sonnenazimutwinkel (Nord=0°, pos. in östlicher Richtung) |
| RHORIZON | Höhenwinkel, bis zu dem die Sonne verdeckt wird |
|
RPHIINC |
Einfallswinkel (Rinne + Fresnel) |
|
RPHITRAN |
Trackwinkel / Transversalwinkel |
|
RDNI |
Direktnormalstrahlung |
|
GCNB |
Berechnete Normalstrahl-Einstrahlung |
|
GCB |
Berechnete Strahl-Einstrahlung (horizontale Ebene) |
|
GCD |
Berechnete diffuse Einstrahlung (horizontale Ebene) |
|
GC |
Berechnete Gesamteinstrahlung (horizontale Ebene) |
|
RKT |
Verwendeter Klarheitsindex kT |
Die erste Aufgabe des Sonnenbauteils ist, den Sonnenstand in Abhängigkeit von der geographischen Lage und der Zeit zu bestimmen. EBSILON®Professional nutzt aus der Literatur verfügbare Algorithmen. Für Einzelheiten zu den Berechnungsverfahren wird der Nutzer auf die Literaturhinweise verwiesen. Die genaue Berechnung des Sonnenstands erfordert hochgenaue Algorithmen zum Stand der Planeten. Für die Simulation von Solaranlagen werden diese Algorithmen nicht benutzt. Stattdessen werden vereinfachte Algorithmen angewendet, die die Position zwischen Sonne und Erde approximieren.
Um das zugrunde liegende Berechnungsverfahren zu erläutern, wird der DIN 5034 Algorithmus als Beispiel gegeben. Alle anderen Algorithmen unterscheiden sich hinsichtlich der Formeln für die Zeitgleichung, Deklination, und Sonnenwinkel.
Aus dem Datumswert in DATETIME wird der Tag des Jahres DOY berechnet. Dieser Wert wird normiert zu einem Tageswinkel (in Grad) JS durch
JS = 360*DOY/366 für Schaltjahre
JS = 360*DOY/365 für normale Jahre
Dieser Winkel JS ist wichtig für die Berechnung der Zeitgleichung und der Deklination.
Aufgrund nicht-optimaler Sonnenbewegung ändert sich die Länge des Sonnentages über das Jahr. Die Zeitgleichung (Einheit: Minuten) wird berechnet durch
EoT = 0.0066 + 7.3525*cos((Js+85.9)) + 9.9359*cos((2*Js+108.9)) + 0.3387*cos((3*Js+105.2))
Die Sonnendeklination ändert sich zwischen -23.3° und +23.3° über das Jahr. Die genaue Kurve wird angenähert durch
decl = 0.3948-23.2559*cos((Js+ 9.1)) - 0.3915*cos((2*Js+ 5.4)) - 0.1764*cos((3*Js+26.0))
Für die Sonnenwinkelberechnung muss die Zeit im Sonnenzeitreferenzsystem bekannt sein. In diesem Referenzsystem ist 12:00 an dem Zeitpunkt festgelegt, wenn die Sonne ihren höchsten Winkel über dem Horizont hat (Sonnenmittag). Wenn FTFRAME=0 (Sonnenzeit) ausgewählt ist, ist die Sonnenzeit WOZ ("Wahre Ortszeit”) gleich der Zeit im DATETIME Parameter. Wenn die Zeit als eine aktuelle Ortszeit OZ gegeben ist, muss die Sonnenzeit aus diesem Wert berechnet werden. Die aktuelle Ortszeit ist der offizielle Zeitrahmen innerhalb einer Zeitzone. Im ersten Schritt wird die Ortszeit in die Mittlere Ortszeit übertragen durch
MOZ = OZ - (FTZONE*15° - LONG) / 15° .
Ist die ausgewählte geographische Lage (LONG) genau dieselbe wie der Zeitzonenmeridian (FTZONE*15), dann MOZ=OZ . Die Sonnenzeit WOZ wird dann erhalten durch Korrektur mit der Zeitgleichung
WOZ = MOZ + EoT / 60 min.
Für die Berechnung der Sonnenwinkel wird der Stundenwinkel Omega
omega = ( 12.00 - WOZ ) * 15°.
benutzt. Der Sinus der Sonnenhöhe ist dann
sin(RSHEIGHT) = min(-1, max(1, cos(omega)*cos(LATI)*cos(decl)+sin(LATI)*sin(decl) )).
Der Kosinus des Sonnenazimut ist dann
cos(rsazim) = min(-1, max(1, ( sin(RSHEIGHT)*sin(LATI)-sin(decl) ) / ( cos(RSHEIGHT)*cos(LATI) ) )
Falls WOZ>12.0 oder WOZ<0 dann
RSAZIM = 180 ° + rsazim
sonst
RSAsZIM = 180 ° - rsazim .
Bitte beachten Sie, dass alle Dreiecksfunktionen mit dem Argument in Grad und nicht in Radiant geschrieben sind.
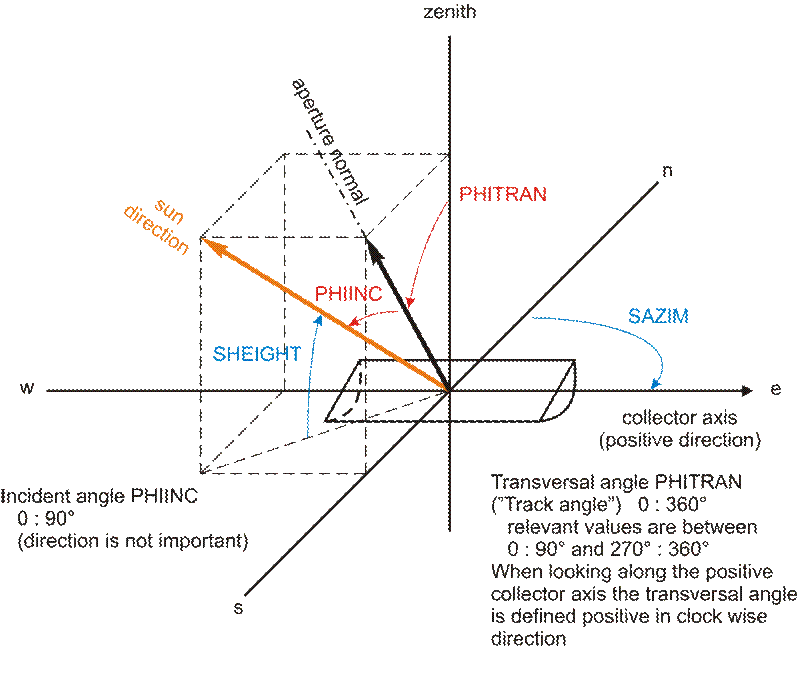
Die folgende Liste verdeutlicht die Benutzeroptionen um den für einachsige Nachführungssysteme relevanten Einfallswinkel und Nachführungswinkel zu berechnen.
Wenn die Berechnung aus dem Einfallswinkel ausgewählt ist, werden die folgenden Formeln aus dem Buch von Stine (1985) benutzt. Der Einfallswinkel wird gegeben als
cos(RSPHIINC) = (1 - ( cos(RSHEIGHT-CSLOP) - cos(CSLOP) * cos(RSHEIGHT) * ( 1-cos(RSAZIM-CAZIM) ) )**2 )**0.5
Der Nachführwinkel (Transversalwinkel für Linear-Fresnel) wird gegeben als
tan(RSPHITRAN) = ( cos(RSHEIGHT)*sin(RSAZIM-CAZIM) ) /
( sin(RSHEIGHT-CSLOP) + sin(CSLOP) * cos(RSHEIGHT) * ( 1 - cos(RSAZIM-CAZIM) ) ) .
Diese Formeln werden auch von Bauteil 113 und 116 benutzt, wenn die entsprechenden Flags aktiviert sind.
Wenn der DNI bekannt ist, kann er über den Parameter DNI spezifiziert oder über eine Logikleitung am Anschluss 1 in das Bauteil übertragen werden.
Gibt es horizontale Einstrahlzahlen, kann FDNI=4 verwendet werden und GHB und GHD angegeben werden.
Alternativ dazu gibt es zwei Methoden zur Abschätzung der Sonneneinstrahlung als Funktion des Ortes und der Zeit:
Wie der Name schon andeutet berücksichtigt das Clear Sky Model keine Effekte der Bewölkung. Es schätzt daher nur die Auswirkungen der Atmosphäre (Standardatmosphäre mit 23 km Sichtweite) auf die Streuung und Absorption der Strahlung ab. Der einzige Parameter ist die Höhe über dem Meeresspiegel, die sich auf die Weglänge durch die Atmosphäre auswirkt.
Der Clearness Index beschreibt das Verhältnis der gesamten Himmelsstrahlung (direkt, diffus und Abstrahlung) zur Weltraumstrahlung bezogen auf eine ebene horizontale Fläche. Der Clearness Index KT kann auch die Effekte der Bewölkung enthalten. Um den Maximalwert für KT zu bestimmen, kann man den Wert für KT durch das Clear Sky Modell berechnen.
DIN 5034
Deutsche Norm DIN5034, Teil 2, Februar 1985, Beuth Verlag GmbH, Berlin
Duffie/Beckmann (1981)
Duffie, Beckman: Solar Engineering of Thermal Processes, Wiley-Interscience, New York, 1991. Es werden auch Teile der DIN 5034 verwendet.
NREL SOLPOS
Sonnenstandsalgorithmus des National Renewable Energy Laboratory in der Version von März 1998. Die Lichtbrechungskorrektur-Option dieses Algorithmus ist in EBSILON®Professional nicht aktiviert.
Stine (1985)
Stine, Harrington: Solar Energy Fundamentals and Design with Computer Applications. Wiley-Interscience, New York, 1985
Iqbal (1983)
Iqbal: An introduction to solar irradiation. Academic Press, New York, 1983
Hottel (1976)
Hottel, H.C.: A Simple Model for Estimating the Transmittance of Direct Solar Radiation Through Clear Atmospheres, Solar Energy, 18, 129 (1976)
Liu and Jordan (1960)
Liu, B. Y. H. and Jordan, R. C.: The Interrelationship and Characteristic Distribution of Direct, Diffuse and Total Solar Radiation, Solar Energy, 4 (3), 1 (1960).
 |
Form 1 |
 |
Form 2 |
 |
Form 3 |
 |
Form 4 |
Klicken Sie hier >> Bauteil 117 Demo << um ein Beispiel zu laden.