

|
Leitungsanschlüsse |
|
|
|
1 |
Fluid Eintritt |
|
|
2 |
Fluid Austritt |
|
|
3 |
Grenzwerteingang |
|
|
4 |
Logik-Ausgang |
|
Allgemeines Vorgabewerte Verwendete Physik Sonnenzufuhr: QSOLAR Kennlinien Bauteilform Beispiel
Dieses Bauteil stellt einen einzelnen linienfokussierenden Solarkollektor dar, der vom Parabolrinnen- oder Linear Fresnel-Typ sein kann.
Für die gängigsten Systeme (Eurotrough, LS-2, IST bei Parabolrinnen, Industrial Solar (früher Mirroxx) bei Fresnel) sind die Daten in einer Datenbank hinterlegt (Komponenten - Eigenschaftsfenster "Allgemeines" --> "Standardwerte laden").
Die zugrunde liegenden Modelle berechnen die Energiebilanz von direkter Sonneneinstrahlung zu nutzbarer Wärme im Wärmeträgermedium. Solar- und Umgebungsdaten werden von einem Bauteil 117 (Sonne) geliefert. Das Bauteil beinhaltet Modelle mit unterschiedlichem Detaillierungsgrad, die durch verschiedene Flags an- und abgeschaltet werden können. Für Daten zum Wirkungsgrad hat der Nutzer die Möglichkeit, Koeffizienten in Standardformulierungen festzulegen, eine Anpassungsfunktion zu benutzen oder Datentabellen zur Interpolation festzulegen.
Parallel zum thermodynamischen Verhalten enthält das Bauteil einen modellbasierten Ansatz zur Druckverlustberechnung. Empirische Korrelationen für Ein- und Zwei-Phasen-Strom sind verfügbar.
Zur Steuerung der Fokussierung ist ein Logik-Eingang (wie zuvor in Bauteil 116) hinzugefügt worden, um eine Temperaturüberschreitung am Austritt zu vermeiden. Hierzu muss das Flag FFOCUS auf 1 gesetzt werden, und der gewünschte FOCUS-Wert muss als Enthalpie auf (Logikleitung) Pin 3 vorgegeben werden. Wenn nötig, kann dies über einen Regler so geändert werden, dass ein gewünschter Austrittszustand erreicht wird.
Außerdem ist ein Logikausgang 4 für QEFF hinzugefügt worden.
Hinweis zur Berücksichtigung des Windeinflusses:
Da der Einfluss von Windgeschwindigkeit und Windrichtung individuell von der jeweiligen Anlage und der umgebenden Landschaft abhängt, gibt es keine allgemeinen Formeln, um diesen Einfluss zu berechnen. Deshalb hat der Korrekturfaktor CORWIND für den Windeinfluss den Standardwert 1, d.h. es wird kein Windeinfluss berücksichtigt. Falls bekannt ist, wie groß der Windeinfluss ist, kann bei CORWIND der entsprechende Korrekturfaktor für den Windeinfluss manuell eingetragen werden.
Falls sogar bekannt ist, wie der Windeinfluss von Windgeschwindigkeit und Windrichtung abhängt, bietet Ebsilon die Möglichkeit, diese Abhängigkeit in einer Kernelexpression EWIND zu hinterlegen. Damit EWIND verwendet wird, muss der Schalter FWIND auf 1 (Verwendung von EWIND) umgestellt werden.
Für die Erstellung der Kernelexpression stellt das Bauteil folgende Größen als KE-Internals zur Verfügung:
· Einfallswinkel PHIINC
· Transversalwinkel PHITRAN
· Temperatur des Mediums (Mittelwert aus Eintritt und Austritt)
· Umgebungstemperatur TAMB
· Direktnormalstrahlung DNI
· Windgeschwindigkeit VWIND
· Windrichtung AWIND
Ob für VWIND und AWIND die lokalen Werte aus dem Bauteil oder die übergeordneten Werte aus dem Sonnenbauteil verwendet werden, wird durch den Schalter FSWIND bestimmt.
Das Ergebnis der Kernelexpression EWIND muss zwischen 0 und 1 liegen. Dieser Wert wird dann mit dem Vorgabewert CORWIND multipliziert und von 1 abgezogen, um den Wirkungsgrad für den Windeinfluss zu erhalten:
ETAWIND = 1 – CORWIND * EWIND
Bei EWIND=0 ist also kein Windeinfluss vorhanden,
bei EWIND=1 der maximale Windeinfluss.
Der Wirkungsgrad verringert sich dann um einen Anteil CORWIND.
Man beachte, dass historisch bedingt CORWIND bei FWIND=0 und FWIND=1 unterschiedlich interpretiert wird.
Bei FWIND = 0 ist CORWIND der Korrekturfaktor für den Wirkungsgrad (d.h. CORWIND=1 bedeutet keine Korrektur),
bei FWIND = 1 ist CORWIND der Anteil, um den der Wirkungsgrad maximal verkleinert wird (d.h. CORWIND=0 bedeutet keine Korrektur).
|
COLSET |
Geladener Kollektor-Datensatz |
|
FTYPE |
Kollektor - Bauart Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Parabolrinne |
|
LENGTH |
Bruttolänge des Kollektormoduls |
|
AWIDTH |
Brutto-Aperturweite des Kollektormoduls |
|
NRATIO |
Optisch wirksamer Flächenanteil : |
|
LFOCAL |
Brennweite des Kollektors (Parabolrinne) / Höhe des Absorberrohrs über der Spiegelebene (Linear-Fresnel) (verwendet für Endlosrechnung) |
|
DINNER |
Absorberrohrdurchmesser innen |
|
ROWDIST |
Achsenabstand von zwei parallelen Kollektorreihen (verwendet für Abschattungsberechnung) |
|
CDIST |
Kollektorabstand (seriell) |
|
CAZIM |
Azimuthwinkel Kollektor: Richtung der positiven Kollektorachse, Nord=0°, positiv in östlicher Richtung |
|
CSLOP |
Neigungswinkel Kollektorachse: Winkel zwischen Kollektorachse und horizontaler Ebene |
|
FMODE |
Schalter für Berechnungsmodus (Auslegung / Teillast) Wie im Elternprofil (Unterprofil nur optional) Ausdruck |
|
FDP12N |
Methode für die Berechnung des nominalen Druckverlustes Ausdruck =0: Gegeben durch Parameter DP12N |
|
DP12N |
Nominaler Druckverlust (dieser Wert wird verwendet wenn FDP12N=0) |
|
NNODEP |
Knoten für Druckverlustberechnung |
|
FDP12PL |
Methode für die Berechnung des Teillast-Druckverlustes Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: abhängig vom Massenstrom |
|
EDP12PL |
Bei FDP12PL=4 Anpassungsfunktion Teillastdruckverlust im Verhältnis zum nominalen Druckverlust |
|
KS |
Äquivalente Sandrauhigkeit der inneren Oberfläche des Absorberrohrs (dieser Wert wird verwendet wenn FDP12N=1) |
|
ZETA |
Druckverlustkoeffizient für zusätzliche Druckverluste, die nicht von Druckverlustmodell abgedeckt sind (verwendet wenn FDP12N=1) |
|
FOPT0 |
Optischer Spitzenwirkungsgrad (bezogen auf die Netto-Aperturfläche LENGTH*AWIDTH*NRATIO bei PHIINC=0) |
|
CLEANI |
Reinheit der Spiegel als Verhältnis der Ist-Reflektivität zur Nominalreflektivität, die für FOPT0 angenommen wird (Standardwert ist 1, was saubere Spiegel bedeutet) |
|
FFOCUS |
Vorgabe der Fokussierung Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: durch Vorgabewert FOCUS |
|
FOCUS |
Fokussierungszustand des Kollektors (0=nicht fokussiert, 1=fokussiert, dazwischen linear) |
|
CORSHAD |
Korrekturfaktor für Ergebnis des Abschattungsmodells ( 0=keine Abschattung, 1= entsprechend Modell) |
|
FELOSS |
Methode für die Berechnung von optischen Endverlusten und Endgewinnen Ausdruck =0: Endverluste nicht berücksichtigt (auch Endgewinne nicht berücksichtigt) =1: Endverluste berücksichtigt entsprechend Modell und Korrekturfaktor CORELOS =2: Endverluste und Endgewinne an der Einströmungsseite des Kollektors berücksichtigt entsprechend Modell und Korrekturfaktoren CORELOS und COREGAI werden verwendet =3: Endverluste und Endgewinne an der Ausströmungsseite des Kollektors berücksichtigt entsprechend Modell und Korrekturfaktoren CORELOS und COREGAI werden verwendet =4: Endverluste und Endgewinne an beiden Seiten des Kollektors berücksichtigt entsprechend Modell und Korrekturfaktoren CORELOS und COREGAI werden verwendet |
|
CORELOS |
Korrekturfaktor für aus dem Endverlustmodell berechnete optische Endverluste (1=keine Korrektur des Modells) |
|
COREGAI |
Korrekturfaktor für aus dem Endgewinnmodell berechnete optische Endgewinne (1=keine Korrektur des Modells) |
|
FWIND |
Korrekturfaktor für Windeinfluss Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Gegeben durch Faktor CORWIND (Hinweis: Vorgabewerte SVWIND und AWIND bleiben grau hinterlegt, auch wenn FSWIND umschaltet.) =1: Anpassungsfunktion EWIND |
|
CORWIND |
Faktor zur Beschreibung des Windeinflusses auf die optische Leistung Wie im Elternprofil (Unterprofil nur optional) Ausdruck Vorgabewert CORWIND (Standardwert = 1 (keine Korrektur)) |
|
EWIND |
für FWIND=1: Anpassungsfunktion Windeinfluss: Ergebnis: 0...1, Standard ist 0. (siehe Hinweis zur Berücksichtigung des Windeinflusses) function evalexpr:REAL;
|
|
NNODE |
Anzahl der für die Berechnung der Wärmeverluste verwendeten Knoten entlang der Kollektorachse. Die Temperaturdifferenz entlang des Kollektors ist in NNODE Intervalle aufgeteilt. Wärmeverluste werden in der Mitte jedes Abschnitts berechnet. |
|
FSPHI |
Festlegung von Einfalls- und Transversalwinkel Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Gegeben durch Parameter PHIINC und PHITRAN =1: Einfalls- und Transversalwinkel aus Berechnung in übergeordnetem Sonnenbauteil mit dem Index ISUN übernommen =2: Einfalls- und Transversalwinkel aus der Kollektorausrichtung berechnet (gegeben durch Parameter CAZIM und CSLOP), und Sonnenstand bezogen aus übergeordnetem Sonnenbauteil mit dem Index ISUN |
|
PHIINC |
Einfallswinkelvorgabe (dieser Wert wird verwendet wenn FSPHI=0) |
|
PHITRAN |
Transversalwinkelvorgabe (dieser Wert wird verwendet wenn FSPHI=0) |
|
FSDNI |
Definition der Direktnormalstrahlung Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: gegeben durch Parameter DNI =1: Übernahme aus übergeordnetem Sonnenbauteil mit dem Index ISUN |
|
DNI |
Direktnormalstrahlung (dieser Wert wird verwendet wenn FSDNI=0) |
|
FSTAMB |
Definition der Umgebungstemperatur Ausdruck =0: gegeben durch Parameter TAMB =1: Übernahme aus übergeordnetem Sonnenbauteil mit dem Index ISUN |
|
TAMB |
Umgebungstemperatur (dieser Wert wird verwendet wenn FSAMB=0) |
|
FSWIND |
Definition der Windgeschwindigkeit und Windrichtung (FWIND=1) Ausdruck =0: gegeben durch Parameter VWIND und AWIND aus dem Bauteil =1: Übernahme der Werte aus übergeordnetem Sonnenbauteil mit dem Index ISUN
|
|
VWIND |
Windgeschwindigkeit (>0, dieser Wert wird verwendet wenn FSWIND=0) |
|
AWIND |
Windrichtung (Süd->Nord=0°, positiv in östlicher Richtung), Wert im Bereich von 0..360°, dieser Wert wird verwendet wenn FSWIND=0) |
|
ISUN |
Index des Referenz-Solardatenbauteils |
|
FIAM |
Methode für die Berechnung der Einfallswinkelkorrektur Ausdruck =0: Standardpolynom |
|
IAMLA |
Koeffizient für Standardformulierung (longitudinal) (A-Term) (für FIAM=0) |
|
IAML0 |
Koeffizient für Standardformulierung (longitudinal) (konstanter Term) (für FIAM=0) |
|
IAML1 |
Koeffizient für Standardformulierung (longitudinal) (linearer Term) (für FIAM=0) |
|
IAML2 |
Koeffizient für Standardformulierung (longitudinal) ( ^2-Term) (für FIAM=0) |
|
IAML3 |
Koeffizient für Standardformulierung (longitudinal) ( ^3-Term) (für FIAM=0) |
|
IAML4 |
Koeffizient für Standardformulierung (longitudinal) ( ^4-Term) (für FIAM=0) |
|
IAML5 |
Koeffizient für Standardformulierung (longitudinal) ( ^5-Term) (für FIAM=0) |
|
IAMLCOS |
Koeffizient für Standardformulierung (longitudinal) (Kosinus-Term) (für FIAM=0) |
|
IAMT0 |
Koeffizient für Standardformulierung (transversal) (konstanter Term) (für FIAM=0 und FTYPE=1) |
|
IAMT1 |
Koeffizient für Standardformulierung (transversal) (linearer Term) (für FIAM=0 und FTYPE=1) |
|
IAMT2 |
Koeffizient für Standardformulierung (transversal) ( ^2-Term) (für FIAM=0 und FTYPE=1) |
|
IAMT3 |
Koeffizient für Standardformulierung (transversal) ( ^3-Term) (für FIAM=0 und FTYPE=1) |
|
IAMT4 |
Koeffizient für Standardformulierung (transversal) ( ^4-Term) (für FIAM=0 und FTYPE=1) |
|
IAMT5 |
Koeffizient für Standardformulierung (transversal) ( ^5-Term) (für FIAM=0 und FTYPE=1) |
|
IAMTCOS |
Koeffizient für Standardformulierung (transversal) (Kosinus-Term) (für FIAM=0 und FTYPE=1) |
|
EPHIINC |
Anpassungsfunktion für Einfallswinkel. Ergebnis: 0...90° (für FIAM=1) |
|
EPHITRAN |
Anpassungsfunktion für Transversalwinkel. Ergebnis: 0...90° oder 270°...360° (für FIAM=1 und FTYPE=1) |
|
FQLOSS |
Methode für Wärmeverlustberechnung Wie im Elternprofil (Unterprofil nur optional) Ausdruck =0: Standardpolynom |
|
QLOSSA0 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (konstanter Term in dT) |
|
QLOSSA1 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (linearer Term in dT) |
|
QLOSSA2 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (^2 Term in dT) |
|
QLOSSA3 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (^3 Term in dT) |
|
QLOSSA4 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (^4 Term in dT) |
|
QLOSSB0 |
Koeffizient für Standardformulierung Wärmeverlust (DNI-Abhängigkeit) (konst. Term in dT) |
|
QLOSSB1 |
Koeffizient für Standardformulierung Wärmeverlust (DNI-Abhängigkeit) (lin. Term in dT) |
|
QLOSSB2 |
Koeffizient für Standardformulierung Wärmeverlust (DNI-Abhängigkeit) (^2 Term in dT) |
|
QLOSSC1 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (linearer Term in T) |
|
QLOSSC2 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (^2 Term in T) |
|
QLOSSC3 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (^3 Term in T) |
|
QLOSSC4 |
Koeffizient für Standardformulierung Wärmeverlust (keine DNI-Abhängigkeit) (^4 Therm in T) |
|
QLOSSD1 |
Koeffizient für Standardformulierung Wärmeverlust (DNI-Abhängigkeit) (linearer Term in T) |
|
QLOSSD2 |
Koeffizient für Standardformulierung Wärmeverlust (DNI-Abhängigkeit) (^2 Term in T) |
|
EQLOSS |
Anpassungsfunktion für Receiver-Wärmeverluste. Ergebnis: [W/m] erforderlich (für FQLOSS=1) |
|
M1N |
Massenstrom (nominal) |
|
VREFN |
Spezifisches Volumen am Referenzpunkt (nominal) |
Die blau markierten Parameter sind Referenzgrößen für den Teillastmodus. Die Ist-Teillastwerte beziehen sich in den verwendeten Gleichungen auf diese Größen.
Generell sind alle sichtbaren Eingaben erforderlich. Häufig werden jedoch Standardwerte zur Verfügung gestellt.
Für weitere Informationen über die Farbe der Eingabefelder und ihre Beschreibungen siehe Komponenten bearbeiten\Vorgabewerte
Für weitere Informationen über Auslegung vs. Teillast und Nominalwerte siehe Allgemeines\Nominalwerte übernehmen
|
RDNI |
Direkt-Normal-Strahlung |
|
RSHEIGHT |
Sonnenhöhenwinkel (Winkel zwischen Sonnenmittelpunkt und Horizont) |
|
RSAZIM |
Azimutwinkel Sonne (Nord=0°, pos. in östlicher Richtung) |
|
RPHIINC |
Einfallswinkel (Rinne + Fresnel) |
|
RPHITRAN |
Trackwinkel / Transversalwinkel |
|
ETACOLL |
Kollektorwirkungsgrad QEFF / (RDNI*ANET) |
|
RFOCUS |
Verwendeter Wert für FOCUS |
|
QSOLAR |
Eingestrahlte Leistung |
|
QLOSS |
Wärmeverluste Kollektor |
|
QEFF |
Wärmeeintrag |
|
QLSOLAR |
Längenspezifische eingestrahlte Leistung |
|
QLLOSS |
Längenspezifische Wärmeverluste |
|
QLEFF |
Längenspezifischer Wärmeeintrag |
|
QASOLAR |
Flächenspezifische eingestrahlte Leistung, QSOLAR/ANET |
|
QALOSS |
Flächenspezifische Wärmeverluste QLOSS/ANET |
|
QAEFF |
Flächenspezifischer Wärmeeintrag QEFF/ANET |
|
ANET |
Netto-Aperturfläche |
|
TAVER |
Durchschnittliche Kollektortemperatur 0.5*(T1+T2) |
|
KIA |
Einfallswinkel-Korrekturfaktor |
|
KIAINC |
Einfallswinkel-Korrekturfaktor (longitudinaler Teil) |
|
KIATRAN |
Einfallswinkel-Korrekturfaktor (transversaler Teil) |
|
ETASHAD |
Abschattungswirkungsgrad |
|
ETAENDL |
Endverlustwirkungsgrad |
|
ETASPILL |
Spillage-Wirkungsgrad |
|
DP12 |
Druckverlust über Kollektor |
|
RVWIND |
In der Berechnung benutzte Windgeschwindigkeit |
|
RAWIND |
In der Berechnung benutzte Windrichtung |
|
RTAMB |
In der Berechnung benutzte Umgebungstemperatur |
Die Wärmezufuhr in den Fluidstrom wird gegeben durch
M1*(H2-H1) = QEFF.
Diese Gleichung wird sowohl für Parabolrinnen- als auch für Linear-Fresnel-Kollektoren benutzt. Die effektive Wärmezufuhr QEFF hängt ab von der Sonnenwärmezufuhr QSOLAR und den Wärmeverlusten QLOSS.
QEFF = QSOLAR - QLOSS
Die Sonnenzufuhr QSOLAR wird bestimmt durch die Gleichung
QSOLAR = DNI * ANET * FOPT_0 * KIA * FOCUS * ETASHAD * ETAENDL * ETASPILL * ETA_CLEAN
mit den Termen:
DNI Direkt-Normal-Strahlung in W/m**2
ANET Netto-Aperturfläche ANET=LENGTH*AWIDTH*NRATIO
FOPT_0 Optischer Spitzenwirkungsgrad (Parameter FOPT0)
KIA Einfallswinkel-Korrektur (Kosinusverluste bereits eingeschlossen)
FOCUS Fokuszustand des Kollektors
ETASHAD Faktor zum Einbeziehen von Abschattungsverlusten
ETAENDL Faktor zur Korrektur durch die Schaltung bestimmter Endverlusteffekte
ETASPILL Faktor zum Einbeziehen von optischen Verlusten aufgrund von Windeinfluss
ETA_CLEAN Faktor zur Korrektur für tatsächliche Spiegelreinheit ETA_CLEAN=CLEANI
Die Wärmeverluste des Kollektors zur Umgebung werden anhand des längenspezifischen Wärmeverlusts qloss berechnet durch
QLOSS = qloss * LENGTH
Die für die Berechnung der Terme angewendeten Methoden werden im folgenden Abschnitt vorgestellt.
Die Leistung des Kollektors hängt ab von dem Produkt
FOPT0 * LENGTH * AWIDTH * NRATIO.
Da in der Literatur zu findende Leistungsdaten keine eindeutige Struktur haben, stellen Sie bitte sicher, dass FOPT0 immer zusammen mit der entsprechenden Referenzfläche benutzt wird. Das könnte die Bruttofläche sein, wie sie durch LENGTH*AWIDTH gegeben wird, oder die Nettofläche, die um den Faktor NRATIO reduziert wird. Wenn die Bruttofläche als Referenz gemeldet wird, sollte NRATIO gleich 1 sein, um zu korrekten Ergebnissen zu kommen.
Für Linear-Fresnel-Systeme wird AWIDTH als die Breite des Kollektorsystems angesehen. Aufgrund der Facettenstruktur wird NRATIO benutzt, um die Netto-Aperturfläche zu bestimmen. Es ist die Entscheidung des Herstellers, ob die Netto-Aperturfläche als die Fläche definiert wird wenn alle Facetten zum Zenit zeigen oder diejenige der beabsichtigten Fläche bei senkrechter Einstrahlung. Für korrekte Ergebnisse sollte die Definition der Aperturfläche konsistent mit dem Wert des optischen Spitzenwirkungsgrads und den Einfallswinkelkorrekturwerten KIA sein.
Bei Linear-Fresnel-Systemen kann es aufgrund der spezifischen Optik dieser Systeme sein, dass der optische Spitzenwirkungsgrad bei senkrechter Einstrahlung nicht erreicht wird. Der Nutzer hat zwei Optionen, um die Parameter festzulegen:
Der optische Spitzenwirkungsgrad FOPT0 beschreibt den optischen Wirkungsgrad des Kollektors unter den Voraussetzungen:
Abweichungen von diesem idealen Referenzpunkt werden durch eine Anzahl Faktoren beschrieben, die die verfügbare Hitze reduzieren. Diese werden im folgenden beschrieben.
Einfallswinkelkorrektur: KIA
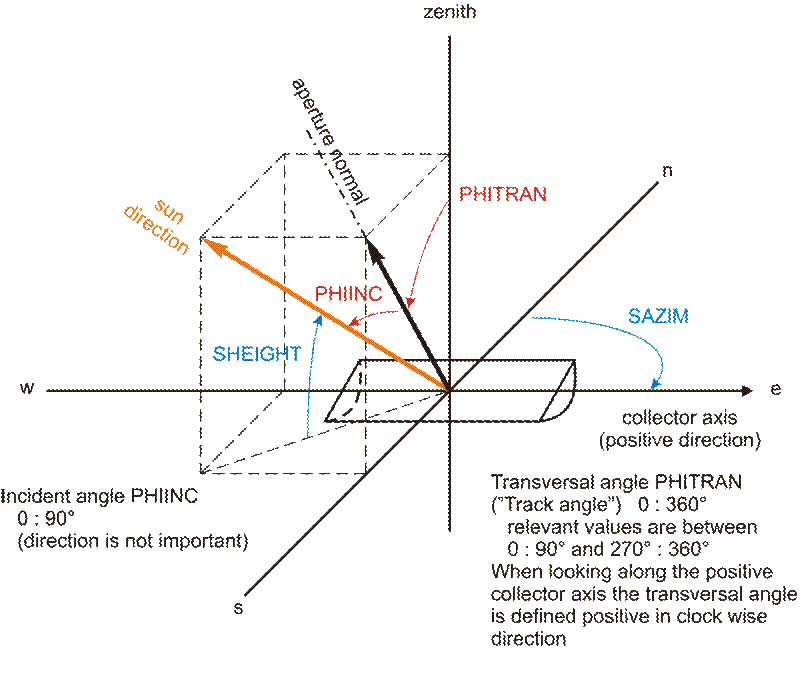
Bei nicht-senkrechtem Sonneneinfall entstehen zusätzliche Verluste durch Abschattung von Strukturelementen des Kollektors, einen längeren optischen Pfad der reflektierten Sonnenstrahlen sowie winkelabhängige Eigenschaften von Spiegeln und Absorberrohr. Diese optischen Effekte sind in der Einfallswinkelkorrektur KIA zusammengefasst. Beachten Sie, dass dieser Faktor bereits die Kosinusverluste von Parabolrinnenkollektoren beinhaltet, um dieselbe Methodologie wie bei Linear-Fresnel-Systemen zu ermöglichen.
KIA = KIAINC(RPHIINC) für Parabolrinnensysteme,
KIA = KIAINC(RPHIINC) * KIATRAN(RPHITRAN) für Linear-Fresnel-Systeme
(mit RPHITRAN=abs(PHITRAN)).
Der Nutzer hat drei Optionen, um die Verhältnisse zwischen den Winkeln RPHIINC, RPHITRAN und KIAINC und KIATRAN, die durch das Flag FSPHI ausgewählt werden, vorzugeben.
KIAINC = ( 1-IAMLA+IAMLA*cos(RPHIINC) ) * (IAMLCOS*cos(RPHIINC) + IAMLO + IAML1*RPHIINC + IAML2*RPHIINC**2 + IAML3*RPHIINC**3 + IAML4*RPHIINC**4 + IAML5*RPHIINC**5 )
Die Struktur dieser Funktion ist so ausgewählt, dass sie in der Literatur gebräuchliche Formulierungen darstellen kann. Die Terme in der ersten Klammer sind notwendig, wenn eine Polynom-basierte Relation für die Einfallswinkelkorrektur dargestellt werden soll, die nicht bereits den Kosinus des Einfallswinkels beinhaltet.
Für die Linear-Fresnel-Systeme werden die Korrelationen
KIAINC = IAMLO + IAML1*RPHIINC + IAML2*RPHIINC**2 + IAML3*RPHIINC**3 + IAML4*RPHIINC**4 + IAML5*RPHIINC**5
KIATRAN = IAMTO + IAMT1*RPHITRAN + IAMT2*RPHITRAN**2 + IAMT3*RPHITRAN**3 + IAMT4*RPHITRAN**4 + IAMT5*RPHITRAN**5
benutzt. In allen Fällen sind die Ergebnisse der Funktionen auf einen Minimalwert von 0 begrenzt. Wenn Sie die Anpassungsfunktion oder tabellenbasierte Methode benutzen, prüfen Sie immer, ob die Einheiten (deg oder rad) von RPHIINC, RPHITRAN zu den Werten passen, die Sie vorgeben.
Wenn die Sonne nahe dem Horizont ist, schatten sich parallele Kollektorreihen gegenseitig ab. Dieser Effekt wird durch den Term ETASHAD berücksichtigt, der auf Grundlage von geometrischer Relation in Abhängigkeit vom Nachführwinkel (=Transversalwinkel) von Parabolrinnensystemen berechnet wird.
ETASHAD=1 - min(1, CORSHAD * max( 0,1- ROWDIST * cos(RPHITRAN) / AWIDTH ) )
Der Term min(...) beschreibt die Reduzierung der verfügbaren Energie als einen Bruchteil der Energie, die zur Verfügung steht, wenn keine Abschattung stattfindet. Wenn die Sonne hoch über dem Horizont steht, ist dieser Term gleich 0 und der ETASHAD ist 1. Der Nutzer hat die Möglichkeit, den modell-basierten Abschattungseffekt durch einen Korrekturfaktor CORSHAD zu korrigieren.
Bei Einfallswinkeln <>0 treffen einige Anteile der reflektierten Sonnenstrahlen an den Enden des Kollektors das Absorberrohr nicht. Dieser Effekt heißt optischer Endverlust und ist eine Funktion des Einfallswinkels RPHIINC. Wenn der nächste Kollektor in derselben Achse ausgerichtet ist, können die verlorenen Sonnenstrahlen eines Kollektors das Absorberrohr des nächsten Kollektors treffen. Ein Teil der verlorenen Wärme kann daher zurückgewonnen werden. Dieser Effekt heißt optischer Endgewinn. Da ein Kollektor einen entsprechenden Nachbarkollektor an einer Seite oder an beiden Seiten haben kann, hängen die effektiven Endgewinne von der Position des Kollektors im Feld ab. Der Nutzer hat die Möglichkeit, vorzugeben, an welchem Ende des Kollektors Endgewinne bezogen werden können. Endgewinne sind immer geringer als die Endverluste. Das Flag FELOSS bestimmt, auf welche Weise mit den Endeffekten umgegangen wird:
Die Endverlusteffekte ETA_ELOS werden berechnet auf Grundlage der Gleichung
ETA_ELOS =1
- CORELOS * min(1, kel * LFOCAL/LENGTH * tan(RPHIINC) )
+ COREGAI * max( 0, keg*min(1, kel * LFOCAL/LENGTH * tan(RPHIINC) ) - CDIST/LENGTH )
wobei der Term mit CORELOS die Endverluste darstellt und der Term mit COREGAI die Endgewinne. Die Parameter CORELOS und COREGAI sind Korrekturfaktoren mit einem Standardwert von 1, der die Effekte um einen Faktor korrigiert. Die Werte kel und keg werden benutzt, um die Nutzerauswahl im Flag FELOSS einzubeziehen:
Für die Berechnung auf Grundlage von FELOSS=2, 3 wird der Sonnenstand (Azimutwinkel SAZIM) benötigt, um den Sonnenstand im Verhältnis zum Kollektor zu bestimmen. Der Sonnenstand muss vom Sonnenmodell mit dem Index ISUN geliefert werden. Für die anderen Optionen wird der Sonnenstand nicht benötigt, um die Endverluste zu berechnen.
Unter Windlasten wird die Kollektorstruktur deformiert, was den optischen Wirkungsgrad reduziert. Dieser Effekt wird dargestellt durch den Faktor ETASPILL. Es ist keine Modell- oder Standardformulierung für den Spillage-Effekt enthalten, da Daten über diesen Effekt spärlich sind. Der Nutzer hat zwei Möglichkeiten:
Die tatsächliche Reinheit der Spiegel im Verhältnis zum ideal reinen Zustand kann durch den Parameter CLEANI vorgegeben werden, so dass ETA_CLEAN=CLEANI.
Aufgrund eines Temperaturunterschieds zwischen dem Wärmeübergangsfluid und der Umgebungsluft treten Wärmeverluste im Kollektor auf. Es wird davon ausgegangen, dass Wärmeverluste nur von dem Temperaturunterschied abhängen. Der Nutzer hat drei Optionen, um den Wärmeverlust qloss pro Längeneinheit des Kollektors vorzugeben:
Die vordefinierte Funktion wird gegeben als
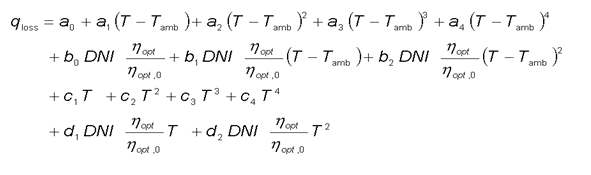
wobei T-Tamb der Temperaturunterschied zwischen Fluid und Umgebung ist, und hopt definiert ist als:
hopt = KIA * FOCUS * ETASHAD * ETAENDL * ETASPILL * ETA_CLEAN .
Die Formulierung der vordefinierten Funktion wird so gewählt, dass aus der Literatur gebräuchliche Formulierungen dargestellt werden können. Die Terme mit QLOSSAx modellieren einen einfachen Wärmeverlust-Term, der nur von der Fluidtemperatur abhängt, was eine vereinfachende Annahme ist. Eigentlich ist der Wärmeverlust abhängig von der Temperatur außen am Absorberrohr. Diese Temperatur hängt daher ab von dem tatsächlichen radialen Wärmestrom, der, in einer ersten Approximation, linear verläuft mit der effektiven Bestrahlungsstärke RDNI*hopt. Die Terme mit QLOSSBx werden hinzugefügt, um diese Einwirkung zu modellieren. Das Polynom zur Berechnung der Wärmeverluste wurde zusätzlich um die direkt von der Temperatur abhängigen Teile erweitert (QLOSSC1 bis QLOSSC4, QLOSSD1, QLOSSD2).
|
QLOSSA0 |
W / m |
|
QLOSSA1 |
W / (m K) |
|
QLOSSA2 |
W / (m K**2) |
|
QLOSSA3 |
W / (m K**3) |
|
QLOSSA4 |
W / (m K**4) |
|
QLOSSB0 |
m |
|
QLOSSB1 |
m / K |
|
QLOSSB2 |
m / K**2 |
|
QLOSSC1 |
W / (m °C) |
|
QLOSSC2 |
W / (m °C**2) |
|
QLOSSC3 |
W / (m °C**3) |
|
QLOSSC4 |
W / (m °C**4) |
|
QLOSSD1 |
m / °C |
|
QLOSSD2 |
m / °C**2 |
Mit der resultierenden Formel können zwei üblicherweise benutzte Formulierungen dargestellt werden. Dies wird im folgenden veranschaulicht:
Die Korrelation für den Kollektorwirkungsgrad, die frühzeitig von Sandia National Laboratories vorgeschlagen wurde, lautet
eta[%] = KIA * (73.3-0.007276*dT) - 0.496*dT / DNI - 0.0691 * dT**2 / DNI .
Um die entsprechenden Werte für die EBSILON®Professional Formulierung zu erhalten, müssen die %-Formulierung und das Vorzeichen berücksichtigt werden. Desweiteren beruht die SANDIA Formulierung auf der Aperturfläche, wohingegen die Formulierung hier längenspezifisch ist. Mit einer Aperturweite für den oben gegebenen LS-2 Kollektor werden die Parameter bezogen als:
|
QLOSSA0, QLOSSA3, QLOSSA4 = 0 |
|
QLOSSA1 = 0.496 W%/(m**2 K) * 5.0 m / 100% = 0.0248 W/ (m K) |
|
QLOSSA2 = 0.0691 W%/(m**2 K**2) * 5.0 m / 100% = 0.003455 W/ (m K**2) |
|
QLOSSB0, QLOSSB2 = 0 |
|
QLOSSB1 = 0.007276 %/K * 5.0 m / 100% = 0.0003638 |
Die Korrelation für die Wärmeverluste eines Eurotrough Kollektors sind veröffentlicht worden als
Qloss[W/m**2] = 0.00047 W/(m**2 K**) * dT**2 .
Dieser flächenspezifische Wärmeverlust kann auf einfache Weise in die längenspezifische Wärmeverlustformulierung überführt werden mit der Nettoaperturweite von 5,45 m (Werte wurden bezogen auf der Grundlage von Nettofläche):
|
QLOSSA0, QLOSSA1, QLOSSA3, QLOSSA4 = 0 |
|
QLOSSA2 = 0.00047 W/(m**2 K**) * 5.45 m = 0.0025615 W/ (m K**2) |
|
QLOSSB0, QLOSSB1, QLOSSB2 = 0 |
Für den Wärmeverlust kann der Anwender die Anzahl der Abschnitte vorgeben, die bei der Berechnung zugrunde gelegt werden (Vorgabewert NNODE). Diese abschnittsweise Berechnung ist auch für den Druckverlust möglich (Vorgabewert NNODEP).
Der Nutzer hat die folgenden Optionen zur Berechnung des Nominal-Druckverlusts:
Der Nutzer hat die folgenden Optionen zur Berechnung des Teillast-Druckverlusts:
Um Ein- oder Zwei-Phasen-Strom mit einem konsistenten Modell abzudecken, wird das Zwei-Phasen-Druckverlustmodell von Friedel (VDI-Wärmeatlas) benutzt. Dieses Modell wird im folgenden beschrieben. Die Berechnung von Druckverlustkoeffizienten basiert auf den Ein-Phasen Reynolds-Zahlen RE_L und RE_G .
RE_L = MFLUX * DINNER / ETA_L
RE_G = MFLUX * DINNER / ETA_G
mit der Massenstromdichte MFLUX=M1/(pi/4*DINNER**2) und den dynamischen Viskositäten von Flüssigkeit (ETA_L) und Gas (ETA_G). Für Zwei-Phasen-Strom werden diese Reynolds-Zahlen berechnet, als ob jede Phase allein im Rohr fließen würde. Die Ein-Phasen-Druckverlustkoeffizienten werden berechnet als
ZETA_L=( 0.86859 * ln( RE_L / (1.964 * ln(RE_L) - 3.8215) ) )**(-2) für RE_L > 1055
ZETA_L=64 / RE_L für RE_L < 1055
ZETA_G=( 0.86859 * ln( RE_G / (1.964 * ln(RE_G) - 3.8215) ) )**(-2) für RE_G > 1055
ZETA_G=64 / RE_G für RE_G < 1055 .
Der Term
DP_L=ZETA_L * MFLUX**2 / (2*DINNER*RHO_L)
beschreibt den spezifischen Druckverlust (Pa/m), als ob die gesamte Masse als Flüssigkeit vorliegen würde. Ein Zwei-Phasen-Multiplikator R wird benutzt zur Berücksichtigung des Einflusses der Gasphase
DP_S = DP_L * R .
Zu Berechnung von R werden die Weber-Zahl
WE_L = MFLUX**2 * DINNER / RHO_L / SIGMA.
und die Froude-Zahl
FR_L = MFLUX**2 / ( 9.81 * DINNER * RHO_L**2 )
der flüssigen Phase benötigt. Mit diesen Zahlen werden die Terme
A = (1-X)**2 + X**2 * (RHO_L * ZETA_G / RHO_G / ZETA_L)
VV = (RHO_L/RHO_G)**0.8 * (ETA_G/ETA_L)**0.22 * (1-ETA_G/ETA_L)**0.89 * FR_L**(-0.047) * WE_L**(-0.0334)
XX = 3.43 * X**0.685 * (1-X)**0.24
= A + XX * VV
berechnet, wobei X der gasförmige Anteil des Stromes ist (kg/s von Gas pro kg/s des Gesamtstroms) und RHO und ETA die Dichte und die dynamische Viskosität von Gas und Flüssigkeit sind.
Dieses Modell kann über den gesamten Bereich von Ein-Phasen-Flüssigkeitsstrom über Zwei-Phasen-Strom bis Ein-Phasen-Gasstrom benutzt werden. Dieses Modell berücksichtigt die Rohr-Rauhigkeit nicht. Da Standardmodelle für Zwei-Phasen-Druckverluste in rauhen Rohren nicht verfügbar sind, wird die folgende Annahme getroffen. In den Ein-Phasen-Regionen wird der Druckverlust in rauhen Rohren berechnet durch die Korrelation
ZETA_LR = 0.25 * ( log10( KS /(3.7*DINNER) + 5.74 /RE_L**0.9 ) )**(-2)
ZETA_GR = 0.25 * ( log10( KS /(3.7*DINNER) + 5.74 /RE_G**0.9 ) )**(-2)
von Swamee und Jain (1976), die die bekannte implizite Gleichung von von Karman und Nikuaradse annähert. Die entsprechenden Druckverluste sind
DP_LR = ZETA_LR * MFLUX**2 / (2*DINNER*RHO_L)
DP_GR = ZETA_GR * MFLUX**2 / (2*DINNER*RHO_G) .
In Ermangelung verlässlicher Modelle wird der Druckverlust in rauhen Rohren in der Zwei-Phasen-Region angenähert als
DP_R = DP_LR + (DP_GR-DP_LR) * X
Der End-Druckverlust wird definiert als das Maximum des Druckverlusts des glatten Rohrs DP_S und des Druckverlusts des rauhen Rohrs DP_R als
DP = max ( DP_S, DP_R) .
Dieser Ansatz hat den Vorteil, dass die Ein-Phasen-Druckverluste sehr gut dargestellt werden. Ein gebräuchliches Modell für den Zwei-Phasen-Druckverlust ist auch verfügbar. Mit dem hier definierten Ansatz ist der Druckverlust stetig an den Rändern X=0 und X=1.
Fluid-Eigenschaften (Enthalpie, Druck, Dampfanteil, ...) für die Druckverlustberechnung werden aus der Mitte des Kollektors genommen.
Zusätzlich zur Druckverlustberechnung für den Strom des Rohrs kann der Nutzer einen Druckverlust-Koeffizient ZETA eingeben zur Erzeugung des zusätzlichen Druckverlusts
DPZETA = ZETA * RHO * ( MFLUX / RHO )**2
Im Falle von Zwei-Phasen-Strom wird die massengemittelte Mischungsdichte RHO benutzt. Die Dichte wird ausgewertet in der Mitte des Kollektors (H1+H2)/2 und (P1+P2)/2.
CIAMINC: Einfallswinkelkorrektur (longitudinal)
Korrekturfaktor = f(PHIINC)
CIAMTRAN: Einfallswinkelkorrektur (transversal)
Korrekturfaktor = f(PHITRAN)
CQLOSSA: Wärmeverlust (dT)
Wärmeverlust = f(dT)
CQLOSSB: Wärmeverlust (dT) / DNI
Wärmeverlust = f(dT) / DNI
 |
Form 1 |
Klicken Sie hier >> Bauteil 113 Demo << um ein Beispiel zu laden.