

Dieses Beispiel ist Abschnitt 7 der Richtlinie VDI 2048, Blatt2, entnommen.
Das Beispiel behandelt die Auswertung der Abnahmemessungen vor und nach Austausch der ND-Teilturbinen in einem Druckwasser-Kernkraftwerk mit Hilfe der Datenvalidierung nach der Richtlinie VDI 2048. Die Vorgehensweise ist dort beschrieben. Auf einer CD werden die Messwerte, Schätzwerte für Spezifikationen und Ergebnisse mitgeliefert.
Hier soll die Behandlung des Beispiel bei Verwendung von EBSILON beschrieben werden.
1. Wasser-Dampf-Kreislauf vor Retrofit in Simulation
Zunächst wird das Modell erstellt und eine Auslegungsrechnung mit den vorgegebenen Daten durchgeführt. Das Ergebnis ist in Bild 10 dargestellt.
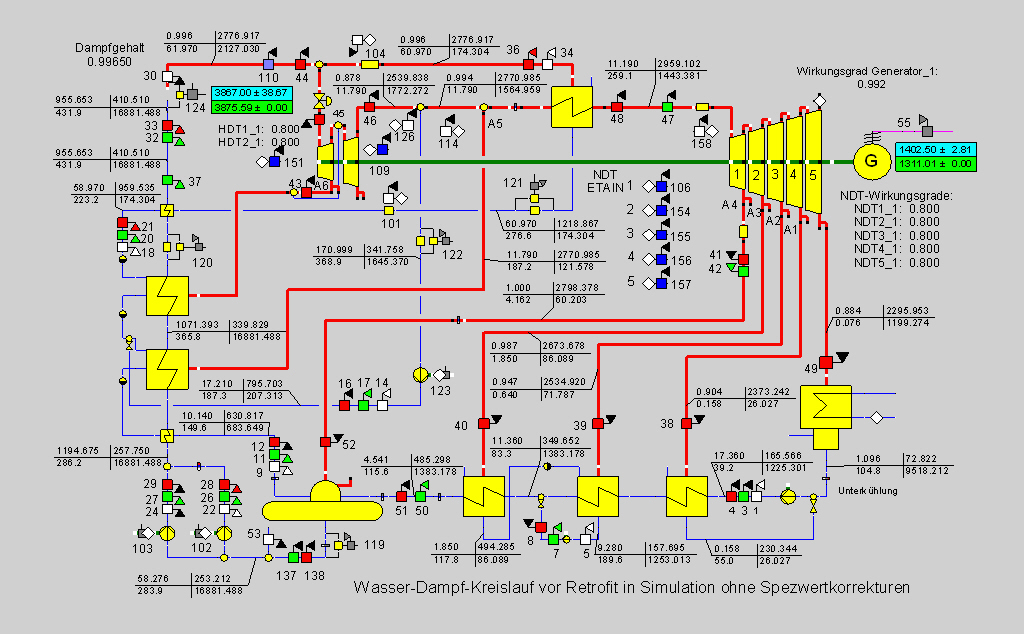
Bild 10
Augenfällig ist die große Differenz der gerechneten Generatorleistung zu ihrem Messwert. Die Ursache ist hauptsächlich in zu kleinen Turbinenwirkungsgraden zu suchen. Zwar kommt auch die Speisewassermessung in Betracht, jedoch erscheint das angegebene Vertrauensintervall zu groß angesetzt, da doch wegen der Einhaltung der genehmigten maximalen thermischen Reaktorleistung diese Messung mit besonderer Sorgfalt kalibriert wird. Da wird dieses Kernkraftwerk im Detail modelliert und über viele Jahre betreut haben (auch während der Retrofitmaßnahme) liegen demgemäß genaue Anlagenkenntnisse vor, die über den Rahmen der Beispielrechnung hinausgehen, aber in unserer Nachrechnung teilweise Eingang finden.
Als erste wesentliche Änderung in den Spezifikationsdaten werden die isentropen Wirkungsgrade angepasst. Für die Hochdruckturbine (2 Scheiben) wurden 0.90 und 0.88 angenommen, was gut mit Herstellermessungen übereinstimmt. Für die Niederdruckscheiben wird ein isentroper Wirkungsgrad von 0.88 angesetzt. Bei Vorgabe der Anzapftemperatur hinter der ersten Scheibe ergibt sich aber ein isentroper Wirkungsgrad von 0.755. Daher wird vor Turbineneintritt ein Rohrleitungswiderstand von 1.2 bar und in der Anzapfung von 0.18 bar vorgesehen. Die Simulationsrechnung ergibt dann für den Wirkungsgrad der ersten Niederdruckscheibe ebenfalls einen Wert von 0.88. Das Simulationsergebnis zeigt Bild 11.
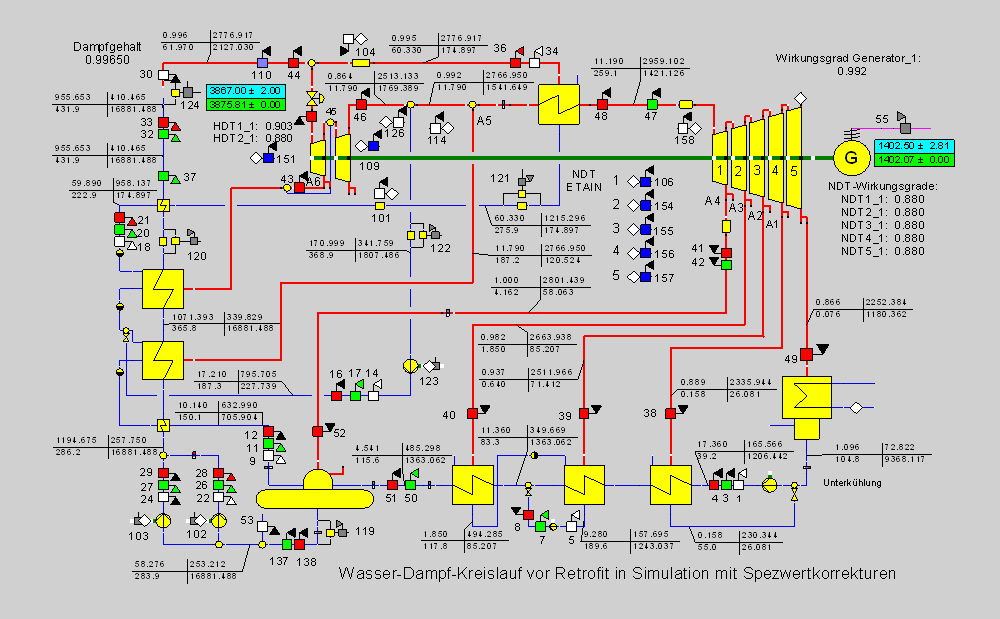
Bild 11
Es zeigt sich eine gute Übereinstimmung für die Generatorleistung. Die folgende Messwertliste zeigt Messwerte und zugehörige gerechnete Werte (SI-Einheiten).
Mess-Stellen Messwert gerechn. Wert Abweichg [%]
-------------------------------------------------------------------
EtaiANZ1_1 0.88000 0.88000 0.00
EtaiANZ2_1 0.88000 0.88000 0.00
EtaiANZ3_1 0.88000 0.88000 0.00
EtaiAnz4_1 0.88000 0.88000 0.00
EtaiHDTA1_1 0.90300 0.90300 0.00
EtaiHDTA2_1 0.88000 0.88000 0.00
EtaiKond_1 0.88000 0.88000 0.00
mHDNK_1 660.470 705.904 -6.44 ?
mHK_1 1206.10 1206.44 -0.03
mKAVHDV_1 203.320 227.739 -10.72 ?
mKZUNKK_1 171.610 174.896 -1.88
mNKNDV_1 155.160 156.619 -0.93
mSPNP1_1 1077.86 1088.23 -0.95
mSPNP2_1 1038.79 1038.79 0.00
mSPVDE_1 2127.03 2127.03 0.00
mZUHD_1 178.880 174.896 2.28
mßISPWB_1 0.00000 0.00000 0.00
pADiK_1 0.07560 0.07560 0.00
pANZ1_1 0.15780 0.15780 0.00
pANZ2_1 0.63980 0.63980 0.00
pANZ3_1 1.85000 1.85000 0.00
pANZ4_1 4.16200 4.16200 0.00
pANZ6_1 23.3900 23.3900 0.00
pASPWB_1 4.01800 4.01800 0.00
Pel_1 1402500 1402066 0.03
pFDNFV_1 60.7300 60.7300 0.00
pFDVFV_1 61.9700 61.9700 0.00
pHDNK_1 10.1400 10.1400 0.00
pHDTA_1 11.7900 11.7900 0.00
pHK_1 17.3600 17.3600 0.00
pHKVSB_1 4.54100 4.54100 0.00
pKAVHDV_1 17.2100 17.2100 0.00
pKZUNKK_1 59.8900 59.8900 -0.00
pNKNDV_1 14.7500 14.7500 0.00
pNZU_1 11.1900 11.1900 0.00
PPuKLWA_1 190.000 175.809 8.07 ?
pSPNP1_1 81.9800 82.3700 -0.47
pSPNP2_1 82.3700 82.3700 0.00
PSpP1_1 10000.0 11508.6 -13.11 ?
PSpP2_1 10000.0 10985.6 -8.97 ?
pSPVDE_1 65.8900 65.8900 -0.00
psSPWB_1 3.81800 3.81800 0.00
PthDEn_1 3867000 3875813 -0.23
pZUHD_1 60.3300 60.3300 -0.00
qWVHDVW_1 60.0000 60.0000 -0.00
qWVKLWA_1 5.00000 5.00000 -0.00
qWVSPWB_1 20000.0 18214.5 9.80 ?
qWVZU_1 50.0000 50.0000 -0.00
tANZ4_1 172.500 172.500 0.00
tASPWB_1 139.941 139.941 -0.00
tHDNK_1 151.200 150.094 0.74
tHK_1 39.1600 39.1600 -0.00
tHKVSB_1 115.600 115.599 0.00
tKAVHDV_1 186.900 187.279 -0.20
tKZUNKK_1 222.600 222.933 -0.15
tNKNDV_1 88.3900 88.0153 0.43
tNZU_1 259.100 259.100 0.00
tSPNP1_1 143.600 141.218 1.69
tSPNP2_1 142.700 141.218 1.05
tSPNZUKK_1 222.550 222.159 0.18
tSPVDE_1 221.850 222.159 -0.14
xFDVFV_1 0.99650 0.99650 0.00
ßmEntn_1 0.94000 0.94000 0.00
ßpHWAZU_1 1.20000 1.20000 0.00
ßpKZUKK_1 0.44000 0.44000 0.00
ßpWAZU_1 0.60000 0.60000 0.00
ßpZUHDL_1 1.64000 1.64000 0.00
Die starken Abweichungen für den Entnässungsstrom und den HD-Nebenkondensat beruhen nach vorliegenden Erfahrungen auf Messfehlern. Für die Pumpenleistungen lagen nur Schätzwerte vor, so dass die gerechneten Werte für die Validierung als Schätzwerte vorgegeben werden. Ansonsten kann festgestellt werden, dass das Simulationsmodell eine gute Abbildung des Prozesses darstellt. EBSILON stellt dabei sicher, dass alle Bilanzgleichungen eingehalten sind.
2. Wasserdampf-Kreislauf vor Retrofit in Validierung
Mit dem in der Simulation erhaltenen Modell einschl. der Spezifikationswerte werden nun die Messwerte und einige Spezifikationsdaten (Entnässungsverhältnis, Turbinen-Wirkungsgrade, Rohrleitungswiderstände) unter Berücksichtigung der zu der Wasserdampftafel IAPWS-IF97 angegebenen Tafelunsicherheiten (International Association for the Properties of Water and Steam, 2003) der Datenvalidierung nach der Richtlinie VDI 2048 unterzogen. Für die Messwerte, für die die Simulation starke Abweichungen aufwies, wurden die Konfidenzintervalle angemessen verbreitert. Ansonsten wird die Verbesserung des anfänglich zu großen Chi2-Testverhältnisses durch Maßnahmen gewonnen, wie sie in vorherigen Beispiel der Durchsatzverteilung (siehe auch Richtlinie VDI 2048 Blatt 2) beschrieben worden sind. Bild 12 zeigt das Endergebnis.
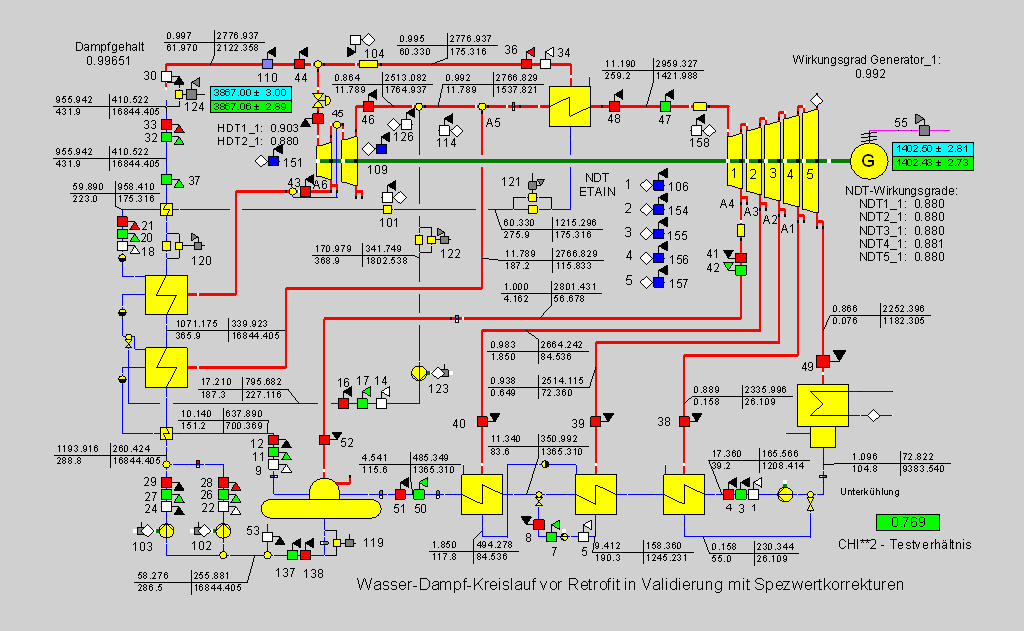
Abbildung 12
3. Wasserdampf-Kreislauf nach Retrofit in Simulation
Es wird genauso verfahren wie vor Retrofit. Die Simulation legt eine Anpassung der isentropen Wirkungsgrade für die Niederdruckturbine nahe. Danach erhält man die in Bild 13 dargestellten Ergebnisse.

Abbildung 13
Ein Blick auf die Liste der Messwerte zeigt einen großen Unterschied für die Entnahmetemperatur A4. Der Grund dafür sind die Wärmeverluste aufgrund der fehlenden Dämmung. Nach nachträglicher Integration der Dämmung, die von uns in das Modell aufgenommen wurde, ergibt sich eine um ca. 20 K höhere Temperatur. Aus diesem Grund muss für die Validierung ein entsprechend breites Vertrauensintervall angesetzt werden.
4. Wasserdampf-Kreislauf nach Retrofit in Validierung
Nach den Anpassungen, die aus den Simulationsrechnungen resultierten, ergibt sich zunächst ein Chi2-Testverhältnis von über 40. Die in der Richtlinie VDI 2048 vorgeschlagenen Maßnahmen zur Justierung der Konfidenzintervalle führen schließlich zu dem Ergebnis von Bild 14.

Abbildung 14
Damit stehen nun für die beiden Anlagenzustände gute Validierungsmodelle zur Verfügung.
5. Zusammenführung der Modelle
Um Korrelationen zwischen den Messwerten, die mit derselben Instrumentierung am gleichen Ort aufgenommen wurden, einführen zu können, müssen die beiden Rechenmodelle für die Zustände vor und nach Retrofit in einer Schaltung zusammengeführt werden, d.h.die beiden Anlagenzustände werden gemäß Abschnitt 7.3 VDI 2048 Blatt 1 in ein EBSILON-Modell zusammengeführt und einer gemeinsamen Validierung unterzogen. Aus der VDI-Beispieldokumentation werden die Korrelationskoeffizienten entnommen und in der dafür vorgesehenen EBSILON-Maske (Rechnen\Kovarianzmatrix) eingetragen. Als weitere Aufgabe ist Wahrscheinlichkeit für die Erfüllung der Garantie einer elektrischen Leistungserhöhung um 32 MW zu berechnen, ferner die Leistungserhöhung mit einer Wahrscheinlichkeit von 80 %.
Entsprechend der VDI-Beispielbeschreibung sind die Generatorleistungen auf einen Referenzkondensatordruck umzurechnen. Eine weitere Korrektur ergibt sich aus der Umrechnung auf die Referenzdampferzeugerleistung. Die Konfidenzintervalle für die berechneten Größen ergeben sich aus dem Fehlerfortpflanzungsgesetz.
Diese zusätzlichen Berechnungen werden in einem EbsScript-Programm behandelt.
// Program for Retrofit-Validation
// with conversion to nominal pressure and same DE-power
// and probability for maintaining the guarantee
var
ier: integer; // Error flag
i,j: integer; // Run-time variable
pgen1,pgen2: real; // Generator power
u1,u2: real; // Conversion factors for DE-power
delpgen: real; // Difference of generator powers
s1,s2,s: real; // Standard deviations
wn:array[1..11] of real; // Distribution function
zw:array[1..11] of real; // Abscissa values
arg: real; // Argument for distribution function
du,du1,du2,du3,du4: real; // Auxiliary quantities
wg: real; // Probability for guarantee fulfillment
pgen80: real; // Generator power with 80 % probability
qn: real; // Nominal DE-power
up1,up2: real; // Conversion factors to nominal pressure
dup1,dup2,sq: real; // Standard deviations
//
begin
// Distribution function of normal distribution
wn[1]:=0; // Integral values of normal distribution
wn[2]:=0.0013;
wn[3]:=0.0228;
wn[4]:=0.1587;
wn[5]:=0.3085;
wn[6]:=0.5;
wn[7]:=0.6915;
wn[8]:=0.8413;
wn[9]:=0.9772;
wn[10]:=0.9987;
wn[11]:=1;
zw[1]:=-1000; // Abscissa values
zw[2]:=-3;
zw[3]:=-2;
zw[4]:=-1;
zw[5]:=-0.5;
zw[6]:=0;
zw[7]:=0.5;
zw[8]:=1;
zw[9]:=2;
zw[10]:=3;
zw[11]:=1000;
//
qn:=3867000; // thermal nominal power
up1:= 1.0140; // Condenser pressure conversion factor for generator power
up2:= 0.9976;
// Confidence intervals for up1,up2
dup1:=0.0002;
dup2:=0.0002;
//
// Conversion of generator power
// to nominal waste steam pressure of 0.058 bar
pgen1:=Pel_1.result*up1;
pgen2:=Pel_2.result*up2;
// Confidence intervals of generator power
s1:=Pel_1.rconf;
s1:=s1*s1;
s1:=s1*up1*up1+Pel_1.result*Pel_1.result*dup1*dup1;
s2:=Pel_2.rconf;
s2:=s2*s2;
s2:=s2*up2*up2+Pel_2.result*Pel_2.result*dup2*dup2;
// Conversion to nominal DE-power of 3867 MW
u1:=qn/PthDEn_1.result;
u2:=qn/PthDEn_2.result;
pgen1:=pgen1*u1;
pgen2:=pgen2*u2;
// Difference of the converted generator powers
delpgen:=pgen2-pgen1;
// Error calculation
// Confidence intervals for the calculated generator power before retrofitting
sq:=PthDEn_1.rconf;
sq:=sq*sq;
du1:=qn/PthDEn_1.result;
du1:=du1*du1;
du2:=pgen1*qn/(PthDEn_1.result*PthDEn_1.result);
s1:=s1*du1+sq*du2;
// Confidence intervals for the calculated generator power after retrofitting
sq:=PthDEn_2.rconf;
sq:=sq*sq;
du1:=qn/PthDEn_2.result;
du1:=du1*du1;
du2:=pgen2*qn/(PthDEn_2.result*PthDEn_2.result);
s2:=s2*du1+sq*du2;
s:=sqrt(s1+s2);
// Probability for guarantee fulfillment
// Guarantee value = 32.1 MW
// Argument of the normal distribution function
arg:=(delpgen-32100)/s;
//print(arg);
j:=1;
i:=0;
wg:=0.9999;
while ((j > 0) and (i < 10)) do
begin
i:=i+1;
if arg < zw[i] then
begin
i:=i-1;
if i = 0 then
begin
wg:=0.0001;
end
else
begin
du:=(arg-zw[i])/2;
du1:=-zw[i]*zw[i]/2;
du1:=exp(du1);
du2:=-(zw[i]+du)*(zw[i]+du)/2;
du2:=exp(du2);
du3:=-(zw[i]+2*du)*(zw[i]+2*du)/2;
du3:=exp(du3);
du4:=sqrt(2*3.141593);
du4:=du/(3*du4);
du:=du4*(du1+4*du2+du3); // Simpson law
wg:=wn[i]+du;
if wg > 0.9999 then wg:=0.9999;
//print(" ",wg," ",wn[i]," ",du,"\n");
j:=0;
end;
end;
end;
// Performance enhancement with 80 % probability
// Argument of the distribution function for 80 % is 0.842
pgen80:=delpgen-s*0.842;
// Output
@model.error:=ier;
@prof.pgen1:=pgen1/1000;
@prof.pgen2:=pgen2/1000;
@prof.dpg:=delpgen/1000;
@prof.wgp:=wg*100;
@prof.ss:=s/1000;
@prof.pg80:=pgen80/1000;
@prof.profil:=getCalcProfileName;
end;
Bild 15 zeigt das Endergebnis.
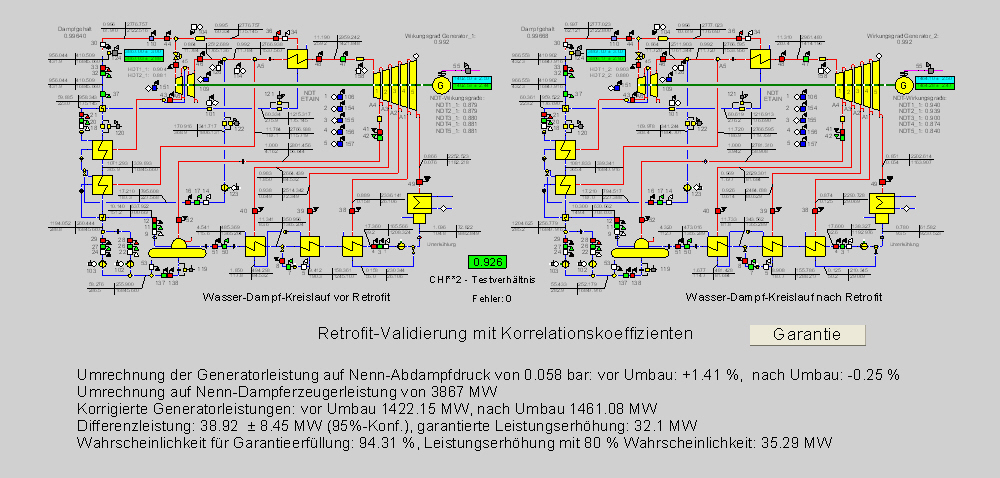
Bild 15
Zur Analyse kann eine vorgefertigte Excelliste über Daten-->Messdaten-->Protokoll-->Validierungsergebnisse (Excel) erstellt werden.
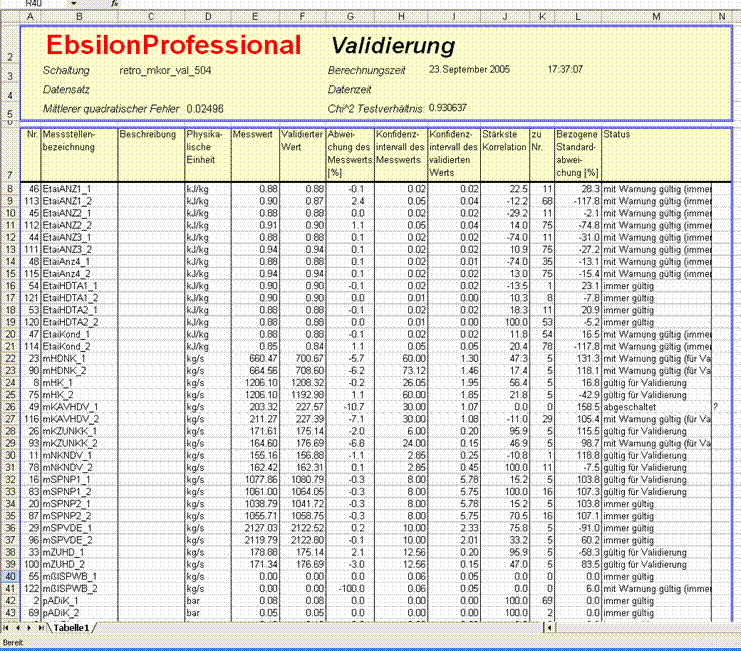
Die Messwertendung "_1" kennzeichnet die Messwerte vor Retrofit, "_2" nach Retrofit.
Für jeden Messwert kann eine Korrelationsliste der Verbesserungen ausgegeben werden (durch rechten Mausklick auf den Messwert). Bei einer vorgegebenen Minimalgrenze für den Korrelationskoeffizienten von 0.1 erhält man beispielsweise für die Messstelle des Frischdampfdurchsatzes folgende Liste:
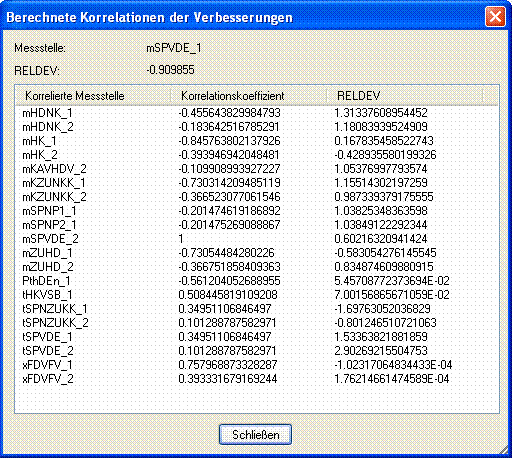
Die Liste kann nach jeder Spaltenüberschrift sortiert werden.