Component 47: Wet Cooling Tower

In This Topic

Component 47: Wet Cooling Tower (with Klenke coefficients)

Specifications

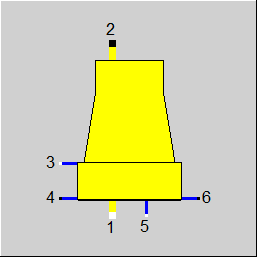
Line connections
1	Air inlet
2	Air outlet
3	Cooling water inlet (warm water)
4	Cooling water outlet (cold water)
5	Make-Up water inlet
6	Blow down

General User Input Values Characteristic Lines Physics Used Displays Example

General

The component "wet cooling tower" simulates the operating performance of wet natural draft cooling towers under nominal and part-load conditions. In the design mode, the user defines a desired cold water temperature and the cooling range is calculated, using the nominal values of the main boundary conditions

Inlet air temperature,
Inlet air humidity,
Warm water inlet temperature,
Water flow rate

In off-design mode, the cold water temperature is calculated as a function of the four main boundary conditions and a performance model developed by KLENKE (BWK, 18, 1966).

To estimate cooling tower performance for natural draft and mechanical draft cooling towers applying performance rules defined in DIN 1947, use components 78 and 79.

Klenke Model

The essential quantities of heat and mass flow can best be modelled by means of an h-x diagram for wet air. The following indices are used to identify the main streams:

1 Air inlet

2 Air outlet

3 Warm water inlet

4 Cold water outlet

4id minimum possible (or ideal) cold water temperature

Other mass flows used in the model are make-up water (M5) and blow down (M6), which are determined from the mass balance equation for water.

M3-M4 = M1*(X2H2O-X1H2O) (1)
M3*H3 - M4*H4 = M1*(H2-H1) (2)

with

M3, M4 Water flow rate
M1 Dry air flow rate
X2H2O, X1H2O Water concentrations on a dry air basis.
H1, H2, H3, H4 Enthalpies

Transformation of equation (1) and (2) results in the definition of the air-to-water ratio (L)

L = M1/M3 = (H3-H4)/(H2-H1 - H4*(X2H2O-X1H2O) (3)

The KLENKE model suggests a description of the cooling tower performance with a single characteristic curve. This characteristic curve correlates the cooling tower effectiveness with the relative air-to-water ratio. The cooling tower effectiveness (α) is defined as the ratio of the actual cooling range to the “ideal” cooling range. The relative air-to-water ratio is defined as the ratio of the actual air-to-water ratio (L) over the “ideal” air-to-water ratio (Lid).

Dependent Variable (y-Axis): α = (T3-T4)/(T3-T4id) (4)

Independent Variable (x- Axis): β = L/Lid (5)

The ideal air-to-water ratio can easily be calculated from equation (3) by using “ideal” conditions for state point 4.

Normally, cooling tower performance needs to be described by a characteristic performance map containing multiple characteristic curves. KLENKE showed in his work that under the condition of a constant ratio of the total mass transfer surface area (surface of all droplets) over the water flow rate a single characteristic curve is sufficient to describe the cooling tower performance.

For simulating the operating performance, it is useful to normalize the characteristic curve around the nominal load point (design case), i.e. use it in terms of α/αN and β/βN.

To describe the design case completely, an input must be provided for the air-to-water ratio (M1/M3) in addition to the four main input parameters. A value of 0.7 is common for natural draft cooling towers.

The calculation of the design case is carried out in the following steps

Input:

Warm water inlet temperature (T3)
Cold water outlet temperature (T4N)
Temperature and humidity of ambient air (T1, PHI1)
Nominal water mass flow (T3N)
Nominal Air-to-water ratio (M1M3N)

Calculation:

T4id (iteration)
T2, X2 from balance equations (iteration)
(M1/M3)id
αN, βN

The off-design calculation is done as follows:

Input:

Warm water inlet temperature (T3)
Temperature and humidity of ambient air (T1, PHI1)
Nominal water flow rate (M3N)
Actual water flow rate (M3)
Nominal cooling range (DT34N)

Calculation:

T4id
M1 by iteration from the cooling tower draft (stack draft)
T2, X2 (iteration)
(M1/M3)id
β from M1 and M3
β/βN and determination of α/αN from the characteristic line
T4 from α/αN and T3 - T4id

User Input Values

M1M3N	Air-to-Water Ratio (nominal) M1N/M3N
T4N	Temperature of cooling water outlet (nominal)
T1	Temperature of air inlet
PHI1	Inlet Air Humidity PHI=Pwater / Psat(T)
MSM3	Drift loss fraction MSpray/M3
M6M3	Blow down mass flow M6/M3
DP34N	Pressure loss (nominal)
CC1	Characteristic lines coefficient 1
CC2	Characteristic lines coefficient 2
CC3	Characteristic lines coefficient 3
FMODE	Flag for calculation mode Like in Parent Profile (Sub Profile option only) Expression =0: Circulation =0: Global =1: local off-design
FSPEC	Make-Up Mode Like in Parent Profile (Sub Profile option only) Expression =0: Circulation mode M3=M4 and M5=M2-M1+M6 =1: Discharge operation (zero Make-Up) M4=M3-(M2-M1+M6) M5=0
DT34N	Cooling range (nominal) DT34N=(T3-T4)N
T1N	Inlet Air Temperature (nominal)
PHI1N	Inlet Air humidity (nominal)
M3N	Cooling water mass flow (nominal)

The parameters marked in blue are reference quantities for the off-design mode. The actual off-design values refer to these quantities in the equations used.

Generally, all inputs that are visible are required. But, often default values are provided.

For more information on colour of the input fields and their descriptions see Edit Component\Specification values

For more information on design vs. off-design and nominal values see General\Accept Nominal values

Characteristic Lines

DTTID = T3-T4id

DTTNID = T3N-T4Nid

DTTNR = DTTN/DTTNID

M1M3NR = M1M3N/M1M3NID

DTTVV = M1M3/M1M3ID/M1M3NR

Characteristic line (DTTVV):

ZW =(DTTV+CC1*(DTTVV^0.3-DTTVV)+CC2*(DTTVV^1.3-DTTVV^2) )* (1+CC3*(T1-T1N)*0.01)

DTT = ZW*DTTID*DTTNR

T4 = T3-DTT

Physics Used

Equations

All cases

M1M3=M1/M3

DTTN=DT34N

Pre-calculation
==============

if GLOBAL = off-design

or iteration > 15, then {calculation of off-design}

H1N = H1

if GLOBAL = Design, then {

T3N = f (P3, H3)

DTTN= T3N-T4N

H3N = H3}

else {

T3N = T4N+DTTN

H3N = f (P3, T3N)

}

CALL Humidity (PHI1N,T1N,P1,X1i)

T4Nid = T_LIMIT (PHI1N,T1N,P1,X1i)

H4N = f (P4,T4N)

INDI = 0

H2N = H2_M1M3(PHI1N, T1N, P1N, H1N, X1i, T3N, P3, H3N, T4N, P4, H4N,
M1M3ID, M1M3N, M1M3NR, M1M3, DTTN, DTT, DTTNR, INDI)

M1M3NID= M1M3_ID (T1N, T3N, H1N, H3N, T4Nid, X1i, X2i)

Reference values of characteristic lines {

DTTNID = T3N-T4Nid

DTTNR = DTTN/DTTNID

M1M3NR = M1M3N/M1M3NID

}

Assignments {

H1X = H1N

H2X = H2N

H4X = H4N

H6X = H4N

DTT = DTTN

M1M3 = M1M3N

}

Calculation of partial load

==========================

T3 = f (P3,H3)

CALL Humidity (PHI1,T1,P1,X1i)

T4id = T_LIMIT (PHI1,T1,P1,X1I)

DTTID = T3-T4id

M1M3ID = M1M3_ID (T1, T3, H1, H3, T4id, X1I, GEW2)

INDI = 2

H2N = H2_M1M3(PHI1N, T1, P1, H1, X1I, T3, P3, H3, T4, P4, H4,
M1M3ID, M1M3N, M1M3NR, M1M3, DTTID, DTT, DTTNR, INDI)

Assignments {

H1X = H1

H2X = H2

H4X = H4

H6X = H4

DTT = T3-T4

}

Equations for pressure

========================

F = 1.0

F = (M3/M3N) ** 2 at MODE = 1

DP34 = DP34N * F

P4 = P3 - DP34

P2 = P1

P4 = P6

P4 = P5

Equations for enthalpy

=======================

H1 = HX1

H2 = HX2

H4 = HX4

H6 = HX6

Equations for mass flow

=========================

ZWG = (X2H2O-X1H2O)*M1M3

if FSPEC = 0, then {

M3 = M4 }

, else {

M3*(M6M3+ZWG+MSM3) = M4

}

M1 = M1M3*M3

M2 = (1+(ZWG+MSM3)/M1M3)*M1

M6 = M6M3*M3

if FSPEC=0, then {

M5 = (M6M3+ZWG+MSM3)*M3 }

else {

M5 = 0 }

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

Subroutine Humidity

Determine water mass concentration at given pressure,
temperature, and relative humidity

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

Humidity (PHI,T,P,X)

=====================

PS = Psat(t)

PH2O= PS * PHI

YH2O= PH2O/P

XH2O= YH2O*MolH2O/MolSUM

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

Subroutine T_LIMIT

Calculation of the wet bulb temperature at given system
pressure, temperature, and relative humidity

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

T_LIMIT (PHI,T,P,Xi)

===================

H = f (P,T,Xi)

TLIM = T

XLIM_H2O_G= f (P,TLIM) (maximum steam portion)

XLIM_H2O = XLIM_H2O_G

Iteration{

DH2O = (MLIM_H2O-M1H2O)/M1

DH2O = (XLIM_H2O-X1H2O)/(1.0-XLIM_H2O)

HLIM= H1+DH2O*(CPWater*TLIM-LH2O)

LH2O=latent heat in water

TLIM= f (HLIM,P)

XLIM_H2O_L=f (P,TLIM) (maximum water portion)

if XLIM_H2O_L >0 then {

XLIM_H2O_G = XLIM_H2O_G-XLIM_H2O_L }

else {

XLIM_H2O_G = f (P,TLIM) (maximum steam portion) }

XLIM_H2O = XLIM_H2O_G

} End of the iteration

T_LIMIT = TLIM

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

Subroutine H2_M1M3

Calculation of the enthalpy of the cooling tower outlet at
given M1/M3 and given thermodynamic state at the
points 1, 3 and 4

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

H2_M1M3 (PHI1,T1,P1,H1,X1i,T3,P3,H3,T4,P4,H4,
M1M3ID,M1M3N,M1M3NR,M1M3,DTTN,DTT,DTTNR,INDI)

T2 = T3

START of the iteration {

CALL humidity (PHI=1,T2,P2=P1,X1i)

if INDI=0, then {

M1M3 = M1M3N (= Ratio M1/M3) }

else {

M1M3 from M1M3N, DENSITY12 , DENSITY12N and

fireplace formula

Characteristic line

DTTVV = M1M3/M1M3ID/M1M3NR

ZW = Characteristic line (DTTVV)

ZW =(DTTV+CC1*(DTTVV^0.3-DTTVV)

+CC2*(DTTVV^1.3-DTTVV^2) )* (1+CC3*(T1-T1N)*0.01)

DTT = ZW*DTTID*DTTNR

T4 = T3-DTT

H4 = f (P4,T4)

}

Energy balance of the cooling tower

ZW2 = (X2H2O-X1H2O)/(1-X2H2O)

H2 = (H1+(H3-H4)/M1M3+(H4-LH2O)*ZW2)/(1-ZW2)

T2 = f (H2,P2)

} End of the iteration

H2_M1M3 = H2

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

Subroutine M1M3_ID

Calculation of the minimal air-to-water ratio M1/M3id for
ideal cooling tower conditions
(i.e. T4=T4_LIMIT, T4=T1 Wet Bulb)

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

M1M3_ID (T1id,T3id,H1,H3,T4_LIMIT,X1i,X2i)

T4id = T4_LIMIT

T2id = T3id

H1id = H1

H3id = H3

H2id = f (P2,T2id)

H4id = f (P2,T2id)

Energy balance of the cooling tower

ZW = (X2_H2O-X1_H2O)/(1-X2_H2O)

M1M3_id = (H3id-H4id)/(H2id-H1id-(H4id-LH2O-H2id)*ZW)

Component Displays

Display Option 1

Example

Click here >> Component 47 Demo << to load an example.

Impressum Disclaimer