

|
Line connections |
|
|
|
1 |
Logical inlet for DNI specification (as H) |
|
|
2 |
Logic outlet for used DNI (as M), incident angle (asP), sun height (as H) and azimuth (as NCV) |
|
General User Input Values Physics Used Displays Example
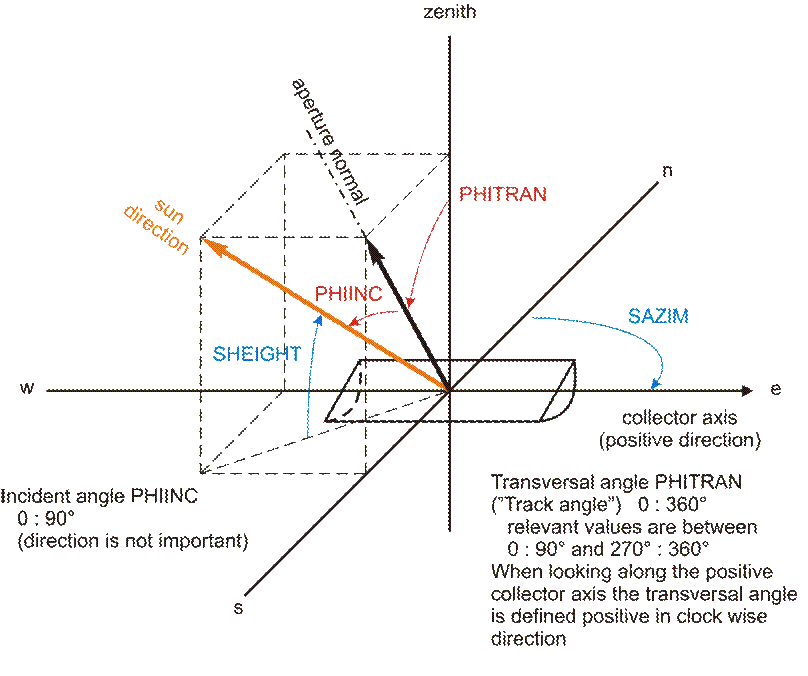
This component provides methods to calculate the sun position and incident angles on single axis tracking surfaces. The user has full flexibility if he wants to calculate these values from geographical data and time or to directly prescribe the angles via specification values. All components referring to the Sun component with index ISUN can, but need not, access these data. Therefore, it is possible to change irradiance data relevant for a number of components in one single component. On the other hand, each component has the functionality to override the values by individual ones. Together with solar irradiation, ambient data can be provided to the respective components.
Although the calculation of incident angles depends on the orientation of each single axis tracking element and should therefore be part of this component's calculation procedure, the user is offered the possibility to perform this calculation already in the Sun component once for all line focusing components.
This component has two optional logic connections:
The output of these variables on a logic outlet enables the application in logic constructions. This allows to use these quantities during the iteration e.g. in controllers and threshold switches.
Please note: in Release 11, DNI was output as mass flow and solar altitude as enthalpy, i.e. there was a different treatment of the DNI on inlet and outlet line. This has been rectified in the context of the new measuring point type FTYP=56 for DNI. In order to prevent resulting changes in logic constructions and controls, a compatibility flag FCOMP has been implemented that has the value 0 when creating a new model, but receives the value 11 when loading a model created with Release 11 (or older).
For FCOMP=11, DNI is output as mass flow and the solar altitude as enthalpy, as before. However, a measuring point with FTYP=56 cannot be used then.
When specifying the DNI via a logic line, the line value is transferred onto the specification value DNI in the design case.
Component 117 contains the CHORIZON characteristic curve and the FHORIZON switch. This allows the silhouette of the horizon to be mapped, i.e. in which direction mountains, trees or houses obscure the sun up to what height (in degrees). With
For reasons of compatibility, the horizon angle is only provided. It is up to the solar components to use this value.
|
FTFRAME |
Time reference system =0: Time is given as solar time (solar noon at 12:00) =1: Time is given in local clock time (daylight savings time is not considered) |
|
FTZONE |
Time zone based on UTC definition in which local time is given (in hours east of Greenwich). This is defined as the longitude of the time zone meridian. (see selection box specification-value) = 12... = 0... ... =-12... |
|
FSANGLE |
Method for calculation of solar position (height and azimuth angle) =0: Not calculated, use parameters SHEIGHT and SAZIM =1: Calculation according to DIN 5034 =2: Calculation according to book of Duffie/Beckmann (1981) =3: Calculation according to NREL SOLPOS (without atmospheric correction) =4: Calculation according to book of Stine (1985) =5: Calculation according to book of Iqbal (1983) =6: Calculation according to NREL SOLPOS (with atmospheric correction) |
|
FIANGLE |
Method for calculation of longitudinal and transversal incident angle (from sun position and collector alignment) =0: Calculation from sun angles =1: Given by specification parameters PHIINC and PHITRAN |
|
LATI |
Latitude of site (positive on northern hemisphere, -90°... 90°) |
|
LONG |
Longitude of site (positive east of Greenwich / -180° to 180°) |
|
DATETIME |
Date and time in the time frame given by FTFRAME |
|
SHEIGHT |
Solar height (angle between the horizontal plane and the sun center) |
|
SAZIM |
Solar azimuth angle (0° due north, positive in eastern direction) |
|
CAZIM |
Collector azimuth angle: Direction of positive collector axis (projection on horizontal plane, 0° is due north, positive in eastern direction). The direction (positive or negative) is of importance for the definition of the track angle. |
|
CSLOP |
Collector slope, angle between collector axis and horizontal plane |
|
PHIINC |
Incident angle (Angle between sun beam and the normal of an single axis tracked surface) |
|
PHITRAN |
Tracking angle of a single axis tracking surface. An angle of 0° means that the surface normal is directed vertically upwards. The angle gets positive if the normal rotates in clockwise direction when looking in positive collector axis. Switching of the axis direction means a change in the sign of the track angle. |
|
FDNI |
Definition of direct irradiance =0: Defined by specification value DNI =1: from logic line "1", line property "enthalpy 1kJ/kg=1 W/m**2" =2: Calculated by clear sky model 23 km view (Hottel 1976) =3: Calculated using clearness index kT =4: Set horizontal Irradiances Please note that logic line "1" has to be activated in tab "fluids" before it can be used. |
|
DNI |
Direct normal irradiance. This value is provided to all components referring to solar parameters ISUN. |
|
GHB |
Global horizontal beam irradiance. This value is provided to all components referring to solar parameters ISUN. |
|
GGD |
Global horizontal diffuse irradiance. This value is provided to all components referring to solar parameters ISUN. |
|
ALTITUDE |
Altitude above sea level. |
|
KT |
Clearness index kT, Ratio of total sky direct solar radiation to space radiation on a horizontal plane. |
| FHORIZON | Horizon Calculations |
|
TAMB |
Ambient temperature. This value is provided to all components referring to solar parameters ISUN. |
|
VWIND |
Wind speed. This value is provided to all components referring to solar parameters ISUN. |
|
AWIND |
Wind direction. From south to north 0°, positive in eastern direction. This value is provided to all components referring to solar parameters ISUN. |
|
ISUN |
Index of the sun component whose data is used for the calculation |
|
FCOMP |
Compatibility mode for logical ports =0: DNI as H on port 1 and 2, height as M on port 2 =11: Release 11: DNI as H on port 1, as M on port 2, height as H on port 2 |
Generally, all inputs that are visible are required. But, often default values are provided.
For more information on colour of the input fields and their descriptions see Edit Component\Specification values
For more information on design vs. off-design and nominal values see General\Accept Nominal values
| Characteristic 1 Name: CHORIZON Title: The elevation angle of the horizon as a function of the azimuth angle. Description: This allows the silhouette of the horizon to be mapped, i.e. in which direction mountains, trees or houses obscure the sun up to what height (in degrees). |
|
Elevation angle of the horizon = f (Azimut angle) |
|
RSHEIGHT |
Sun height (same definition as SHEIGHT) |
|
RSAZIM |
Sun azimuth angle (same definition as SAZIM) |
| RHORIZON | Elevation angle up to which the sun is obscured |
|
RPHIINC |
Incident angle (same definition as PHIINC) |
|
RPHITRAN |
Track / Transversal angle (same definition as PHITRAN) |
|
RDNI |
Direct normal irradiance used for calculation |
|
GCNB |
Calculated normal beam irradiance |
|
GCB |
Calculated beam irradiance (horizontal plane) |
|
GCD |
Calculated diffuse irradiance (horizontal plane) |
|
GC |
Calculated total irradiance (horizontal plane) |
|
RKT |
Clearness index kT used |
The first task of the sun component is to determine the position of the sun in dependence of geographical location and time. EBSILON®Professional makes use of algorithms in literature. For details of the calculation procedures, the user is referred to the literature references. Exact calculation of the sun position requires highly accurate planetary position algorithms. For solar application simulation, these algorithms are not in use. Instead, simplified algorithms that approximate the position between sun and earth are applied.
In order to illustrate the underlying calculation procedure, the DIN 5034 algorithm is given as an example. All other algorithms differ in the formulas for the equation of time, the declination, and the sun angles.
From the date value in DATETIME, the day of the year DOY is calculated. This value is standardized to a day angle (in deg) JS by
JS = 360*DOY/366 for leap years
JS = 360*DOY/365 for regular years
This angle JS is important for the calculation of the equation of time and the declination.
Due to non-optimal sun movement, the solar day changes in length over the year. The equation of time (unit is minutes) is calculated by
EoT = 0.0066 + 7.3525*cos((Js+85.9)) + 9.9359*cos((2*Js+108.9)) + 0.3387*cos((3*Js+105.2))
The solar declination changes between -23.3° and +23.3° over the year. The exact curve is approximated by
decl = 0.3948-23.2559*cos((Js+ 9.1)) - 0.3915*cos((2*Js+ 5.4)) - 0.1764*cos((3*Js+26.0))
For sun angle calculation, the time has to be known in the solar time reference system. In this reference system 12:00 is fixed to the instant when the sun has its highest angle over the horizon (solar noon). In case FTFRAME=0 (Solar time) is selected, the solar time WOZ (from German term "Wahre Ortszeit") is equal to the time in the DATETIME parameter. In case the time is given as a local clock time OZ (from German "Ortszeit"), the solar time has to be calculated from this value. The local clock time is the official time frame within a time zone. In the first step, the local time is transferred into the mean local time ("Mittlere Ortszeit") by
MOZ = OZ - (FTZONE*15° - LONG) / 15° .
If the selected geographical position (LONG) is exactly the same as the time zone meridian (FTZONE*15) then MOZ=OZ . The solar time WOZ is then obtained by correction with the equation of time
WOZ = MOZ + EoT / 60 min .
For calculation of the sun angles, the hour angle omega
omega = ( 12.00 - WOZ ) * 15°.
is used. The sine of the sun height is then
sin(RSHEIGHT) = min(-1, max(1, cos(omega)*cos(LATI)*cos(decl)+sin(LATI)*sin(decl) )).
The cosine of the sun azimuth is then
cos(rsazim) = min(-1, max(1, ( sin(RSHEIGHT)*sin(LATI)-sin(decl) ) / ( cos(RSHEIGHT)*cos(LATI) ) )
In case WOZ>12.0 or WOZ<0 then
RSAZIM = 180 ° + rsazim
else
RSAZIM = 180 ° - rsazim .
Please note that all triangular functions are written with the argument in degrees not in radians.
The following list illustrates the user options to calculate the incident and track angle relevant for single axis tracking systems.
In case calculation of the incident angle is chosen, the following formulas from the book of Stine (1985) are used. The incident angle is given as
cos(RSPHIINC) = (1 - ( cos(RSHEIGHT-CSLOP) - cos(CSLOP) * cos(RSHEIGHT) * ( 1-cos(RSAZIM-CAZIM) ) )**2 )**0.5
The track angle (transversal angle for linear Fresnel) is given as
tan(RSPHITRAN) = ( cos(RSHEIGHT)*sin(RSAZIM-CAZIM) ) /
( sin(RSHEIGHT-CSLOP) + sin(CSLOP) * cos(RSHEIGHT) * ( 1 - cos(RSAZIM-CAZIM) ) ) .
These formulas are also used by components 113 and 116 if the corresponding flags are activated.
If the DNI is known, it can be specified with the parameter DNI or it can be transferred via a logic line connected to port 1. If the horizontal Irradiances (beam and diffuse) are measured FDNI=4 can be used.
There are two methods to estimate the solar irradiation as a function of the specified location and time:
As the name indicates, the Clear Sky Model does not account for effects of clouds, thus it estimates the impact of the atmosphere with 23 km visibility on scattering and absorbing the radiation. The only parameter of this model is the altitude above sea level which affects the path length through the atmosphere.
The Clearness Index describes the ratio of the total sky direct solar radiation to the extraterrestrial radiation on a horizontal plane. The clearness index KT may also include the effect of clouds. In order to find the maximum value for KT, the value for KT resulting from a clear sky can be calculated from the Clear Sky Model.
DIN 5034
German standard DIN5034, part 2, February 1985, Beuth Verlag GmbH, Berlin
Duffie/Beckmann (1981)
Duffie, Beckman: Solar Engineering of Thermal Processes, Wiley-Interscience, New York, 1991. Parts of DIN 5034 are used, too.
NREL SOLPOS
National Renewable Energy Laboratory Solar Position Algorithm in the version of March 1998. The refraction correction option of this algorithm is not activated in EBSILON®Professional .
Stine (1985)
Stine, Harrington: Solar Energy Fundamentals and Design with Computer Applications. Wiley-Interscience, New York, 1985
Iqbal (1983)
Iqbal: An introduction to solar irradiation. Academic Press, New York, 1983
Hottel (1976)
Hottel, H.C.: A Simple Model for Estimating the Transmittance of Direct Solar Radiation Through Clear Atmospheres, Solar Energy, 18, 129 (1976)
Liu and Jordan (1960)
Liu, B. Y. H. and Jordan, R. C.: The Interrelationship and Characteristic Distribution of Direct, Diffuse and Total Solar Radiation, Solar Energy, 4 (3), 1 (1960).
 |
Display Option 1 |
 |
Display Option 2 |
 |
Display Option 3 |
 |
Display Option 4 |
Click here >> Component 117 Demo << to load an example.