

|
Leitungsanschlüsse |
|
|
Allgemeines Vorgabewerte Ergebnisse Bauteilform Beispiel
Mithilfe dieses Bauteils werden für eine oder mehrere Windturbinen (Bauteil 143) relevante Winddaten spezifiziert und gerechnet.
Die Beziehung zwischen der Leistung P einer Windturbine, der ungestörten Windgeschwindigkeit v1 auf der Nabenhöhe, und dem Leistungsbeiwert cP ist wie folgt
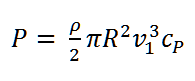
Die Nabenhöhe liegt bei modernen Windturbine typischerweise bei 100 m oder höher. Da die ungestörte Windgeschwindigkeit v1 als Messwert auf der Nabenhöhe für eine erst geplante Anlage nicht vorliegt, wird diese aus vorhandenen Daten (meistens über mehrere Jahre gemittelte Messungen auf 10 m Höhe) ausgerechnet. Die Abbildung 1 zeigt die schematische Darstellung des logarithmischen vertikalen Geschwindigkeitsprofils und den Zusammenhang zwischen den Windgeschwindigkeitswerten auf unterschiedlichen Höhen.
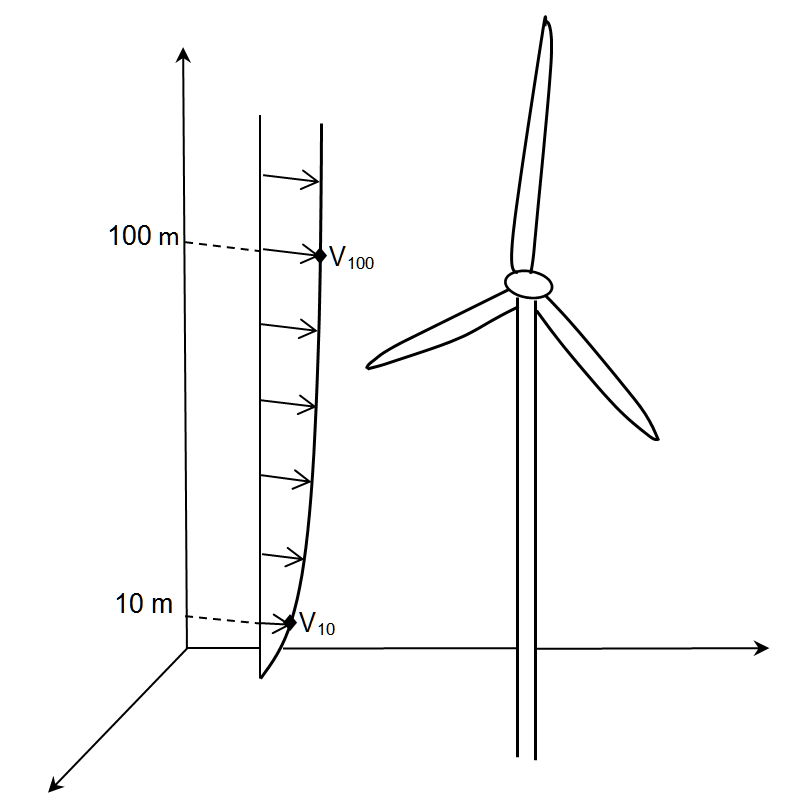
Abbildung 1: Schematische Darstellung des logarithmischen vertikalen Geschwindigkeitsprofils unter Annahme der Prandtl-Grenzschicht
Die Umrechnung kann nach verschiedenen Rechenalgorithmen erfolgen. Die einfachste Methode basiert auf der Annahme eines logarithmischen vertikalen Geschwindigkeitsprofils (Prandtl’sche Grenzschicht, siehe Abbildung 1). Ein komplexer Algorithmus berücksichtigt zusätzlich den Einfluss der atmosphärischen Schichtung. Dieser Einfluss hängt mit dem vertikalen Temperaturprofil der Luft in Bodennähe zusammen. Dabei wird zwischen 3 Kategorien unterschieden (siehe Abbildung 2). Bei labiler Schichtung ist die bodennahe Luft wärmer als die darüber liegende (typisch für Sommermonate bei starker Erwärmung des Bodens). Bei stabiler Schichtung ist die Lufttemperatur am Boden niedriger als in den darüber liegenden Schichten (typisch für Wintermonate, wenn der Boden stark abkühlt). Bei neutraler Schichtung liegt weder Erwärmung noch eine Abkühlung in der bodennahen Luftschicht vor. Um den Einfluss der atmosphärischen Schichtung zu berücksichtigen, werden unter anderem die Daten der Jahreszeit, der Sonnenposition und der Bewölkung benötigt. Da diese Daten charakteristisch für einen Ort sind, ist es ausreichend die Berechnungen in einem Bauteil 142 durchzuführen und anschließend für jede Windturbine eines Windparks zu übernehmen.
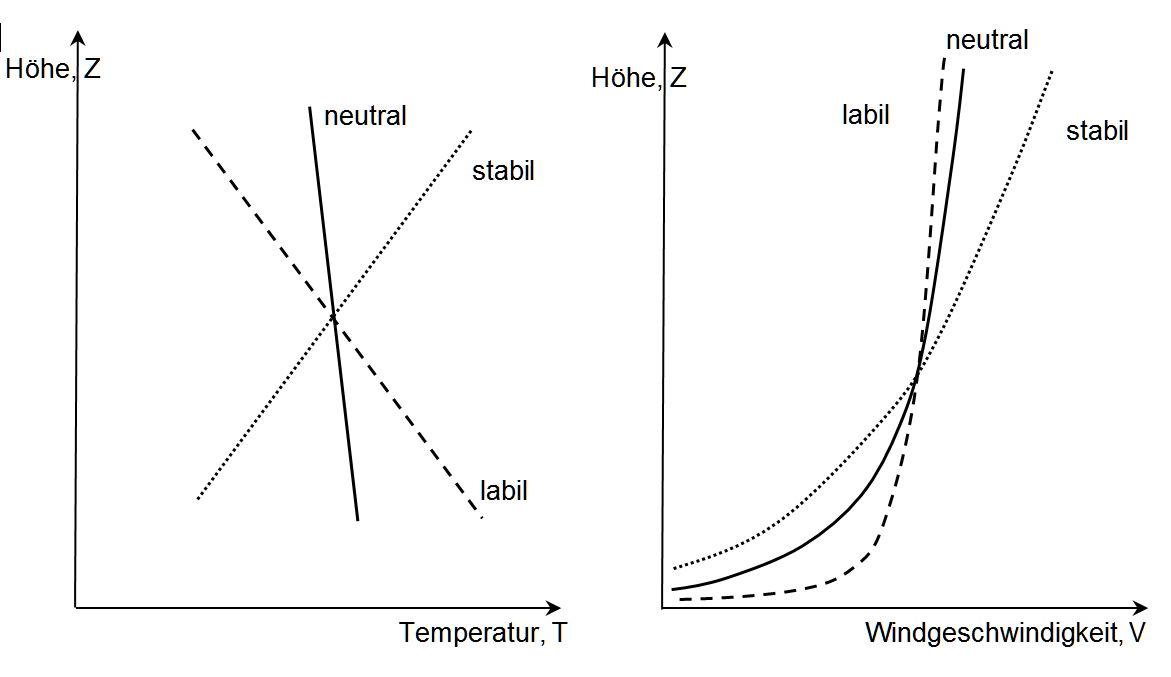
Abbildung 2: Das vertikale Temperaturprofil (links) und das entsprechende Windgeschwindigkeitsprofil (rechts) abhängig von der atmosphärische Stabilität
Die Umrechnung der Windgeschwindigkeit auf Nabenhöhe
Algorithmus 1: Umrechnung ohne Berücksichtigung der atmosphärischen Schichtung (oder für neutrale Schichtung) unter der Annahme, dass die beiden Höhen z1 (die Referenzhöhe, in der die entsprechende Windgeschwindigkeit v1 bekannt ist) und z2 (die Nabenhöhe) sich in der Prandtl-Grenzschicht (Abbildung 1) befinden.
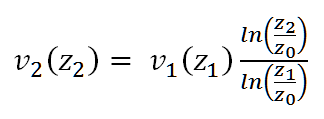
Dabei werden die Rauigkeitslänge z0, die Höhen z1 und z2 und die Geschwindigkeit v1 als Eingaben eingesetzt. Ergebnis ist die Geschwindigkeit v2.
Algorithmus 2: Verfeinerung des Algorithmus 1, Berücksichtigung der atmosphärischen Schichtung.
Zusätzliche Eingaben sind die Gesamtbedeckung in Achteln, Monat und Tageszeit, aus denen die Sonnenposition und die entsprechenden Zeitpunkte für den Sonnenaufgang und den Sonnenuntergang ermittelt werden. Die vorherige Formel wird um eine empirische Stabilitätsfunktion Ψ wie folgt erweitert
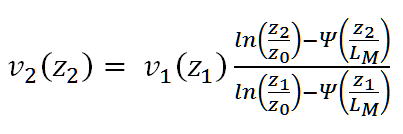
Die Stabilitätsfunktion Ψ hängt von der s.g. Monin-Obukhov-Länge LM ab und korrigiert die Geschwindigkeitsverteilung um die entsprechende Temperaturschichtung. Die genaue Form der Stabilitätsfunktion Ψ ist in [2] zu finden. Die Monin-Obukhov-Länge LM lässt sich aus der Bodenrauigkeitslänge z0 und der Ausbreitungsklasse nach Klug / Manier entsprechend der Tabelle 17 aus [3] bestimmen. Die Ausbreitungsklasse nach Klug / Manier ist wiederum von der Windgeschwindigkeit in 10 m Höhe, Gesamtbedeckung in Achtel und der Sonnenposition (Jahreszeit, Nachtstunden, Tagesstunden, Stunden vor und nach dem Sonnenaufgang / Sonnenuntergang) abhängig. Für die Bestimmung der Ausbreitungsklasse nach Klug / Manier wird der in [4] (Anhang A) beschriebene Algorithmus verwendet.
In [1] werden folgende Anhaltswerte für die Bodenrauigkeitslänge z0 empfohlen:
| z0 [m] | Geländetyp |
| 2 | Stadtkerne |
| 1.5 | Vorort, flache Bebauung |
| 0.3-1.6 | Wald |
| 0.1 | Heide mit wenigen Büschen und Bäumen |
| 0.03 | Ackerland |
| 0.0001-0.001 | Ruhige Wasserflächen |
Die Monin-Obukhov-Länge LM kann im Bauteil 142 entweder direkt vom Benutzer vorgegeben oder auf Basis [3]-[4] berechnet werden. Anschließend kann die Monin-Obukhov-Länge aus dem Bauteil 142 in den Bauteilen 143 für die Berechnung der Windgeschwindigkeit in Nabenhöhe nach [2] verwendet werden.
Tabelle 17 aus [3] für die Bestimmung der Monin-Obukhov-Länge LM abhängig von der Ausbreitungsklasse nach Klug/Manier und der Rauigkeitslänge z0 ist im Folgenden dargestellt.
| Ausbreitungsklasse |
Rauigkeitslänge z0 [m] |
||||||||
| nach Klug/Manier | 0.01 | 0.02 | 0.05 | 0.1 | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 |
| I (sehr stabil) | 7 | 9 | 13 | 17 | 24 | 40 | 65 | 90 | 118 |
| II (stabil) | 25 | 31 | 44 | 60 | 83 | 139 | 223 | 310 | 406 |
| III/1 (indifferent) | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 |
| III/2 (indifferent) | -25 | -32 | -45 | -60 | -81 | -130 | -196 | -260 | -326 |
| IV (labil) | -10 | -13 | -19 | -25 | -34 | -55 | -83 | -110 | -137 |
| V (sehr labil) | -4 | -5 | -7 | -10 | -14 | -22 | -34 | -45 | -56 |
Die geographischen Positionen des Ortes werden aus dem BT 117 (Sonne) übernommen. Das Gleiche betrifft die Angabe der Zeit bei der Berechnung mit Zeitreihen-Dialogen. Daraus werden die Sonnenposition und die Ausbreitungsklasse nach Klug / Manier nach [4] ermittelt.
Da im Bauteil 143 (Windturbine) die Leistungskennlinie des Herstellers sich auf die nach IEC 61400-12-1 normierte Windgeschwindigkeit bezieht, ist es erforderlich, die für die Normierung nach IEC 61400-12-1 benötigten Lufttemperatur und Luftdruck zu kennen. Diese Werte sind auch gleich für alle Windturbinen des Windparks und werden daher in einem BT 142 spezifiziert.
Referenzen
[1] Windkraftanlagen. Grundlagen, Entwurf, Planung und Betrieb. R. Gasch, J. Twele 8 Auflage
[2] VDI 3783 Blatt 8: Umweltmeteorologie Messwertgestützte Turbulenzparametrisierung für Ausbreitungsmodelle
[3] Technische Anleitung zur Reinhaltung der Luft – TA Luft 2002
[4] VDI 3782 Blatt 1: Umweltmeteorologie Atmosphärische Ausbreitungsmodelle. Gauß’sches Fahnenmodell für Pläne zur Luftreinhaltung
|
ISUN |
Index des Referenz-Solardatenbauteils (Bauteil 117) |
|
IWDATA |
Index für das aktuelle BT 142 für die Verwendung in BT 143 |
|
VWIND |
Windgeschwindigkeit |
|
AWIND |
Windrichtung (Süd ->Nord =0° (positiv in östlicher Richtung) |
|
HVWIND |
Höhenangabe für VWIND |
|
CLCOVE |
Gesamtbedeckung in Achteln |
|
VWIND10M |
Angabe der Windgeschwindigkeit in 10 m Höhe in m/s (wird bei der Berechnung der Monin-Obukhov-Länge benötigt) |
|
FLMO |
Behandlung der Monin-Obukhov-Länge =0: Berechnung entsprechend TA Luft, VDI 3782 Bl. 1 und VDI 3783 Bl. 8. aus geog. Position (ISUN), CLCOVE, VWIND10M, Z0 =1: Vorgabe von LMO verwenden |
|
LMO |
Monin-Obukhov-Länge |
|
PREF |
Referenz-Luftdruck (für die Umrechnung der aktuellen Luftdichte auf ISO-Normbedingungen) |
|
TREF |
Referenz-Lufttemperatur (für die Umrechnung der aktuellen Luftdichte auf ISO-Normbedingungen) |
|
Z0 |
Bodenrauigkeit-Länge |
|
RLMO |
Berechnete Monin-Obukhov-Länge |
|
DISPCAT |
Ausbreitungsklasse nach Klug-Manier (siehe dazu Tabelle zur Bestimmung der Monin-Obukhov-Länge) |
 |
Form 1 |
Klicken Sie hier >> Bauteil 142 Demo << um ein Beispiel zu laden.