Preheater Calculation according to Rabek-Method

New preheater model
 

1.  Problem description and motivation

The classical method used for calculation of component 10 (FRABEK =0) assumes that the influence of superheated steam on the heat transfer can be ignored.

 

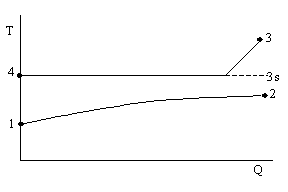
Fig 1: Q-T-Diagram (classical method)

 

  1:       inlet water

  2:       outlet water

  3:       inlet steam

  4:       outlet condensate

3s:       saturation temperature of the pressure P3

 

All relations use temperature  T_3s. for the calculation of temperature differences.

The following disadvantages occur from this:

• Terminal temperature differences (T3S-T2) less than 0.5 °C  (therefore, also terminal temperature differences) result in extreme high (k*A) values and simulate part-load conditions with high inaccuracies.
• For steam super heating in part-load the terminal temperature differences are not calculated correctly.

To cope up with such tasks earlier, desuperheaters had to be modelled as an additional component.

 

2.  Suggested solution

To solve this problem basically a partitioning of heating surface into desuperheating and condensation area is necessary, which can be shifted in case of part load. In (G. Rabek: Die Ermittlung der Betriebsverhältnisse von Speisewasservorwärmern bei verschiedenen Belastungen. Energie und Technik, 1963), a method was published which is using this idea. From this, the following aspects are used in Ebsilon:

• the model for desuperheater and condenser
• the k ratio calculation method

Not used are:

• the integration of the preheater into the component, because this extension is not necessary. Changes of this type may be done later.
• the method of calculation and the solving of equations.

The basis for the used model is the partition into a condenser area and (I) and a super heater area (II) (Fig. 2).

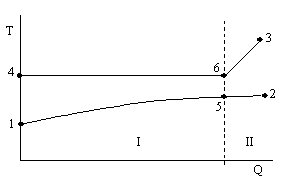
Fig 2: Q-T-Diagram (new model)

1:         inlet water

2:         outlet water

3:         inlet steam

4:         outlet condensate

5:         intermediate point water

6:         begin of condensation of steam

I:          condensation area

II:         desuperheater area

 

Following relations describe the heat transfer process exactly

Q = Q_I + Q_II                                                                                             (1)

Q = k_I A_I Dt_mI + k_II A_II Dt_mII                                                                    (2)

Q:        transferred heat

k:         k - ratio for areas I and II

A:        area

Dtm:    logarithmic temperature difference

 

Known from the energy balance of the steam side are the relation Q_I/Q_II as well as the logarithmic temperature difference, because all temperatures can be calculated.

 

From (2) follows

            Q = k_I A_I  Dt_mI (1 + Q_II/Q_I)                                                                     (3)

as well as

            Q_I/Q_II = (k_I A_I Dt_mI) / (k_II A_II Dt_mII)                                                          (4)

 

(4) modified leads to

            A_II/A_I = Q_II /Q_I Dt_mI/Dt_mII k_I/k_II                                                                (5)

The total area is A comprises of

            A = A_I + A_II = A_I (1 + A_II/A_I)                                                                  (6)

or

            A_I = A / (1 + A_II/A_I)                                                                                (7)

 

The transferred heat according to (2) can, therefore, be written as

            Q = (k_IA) / (1+A_II/A_I) (1+Q_II/Q_I) Dt_mI                                                    (8)

 

(k_I A) equals to the well known value WTKF; Q_II/Q_I results from the heat balance

Steam and A_II / A_I can be calculated from (5).

To be able use equation (8) for

            - k_I    as well as

            - k_I / k_II

relations for full and part load must be derived.

 

For development of these relations a terminology also according to Rabek is used.

            k_I / k_Iv = (1/a_1v+ 1/a_3v) / (1/a₁+ 1/a₃)                                                (9)

            a₁: a- ratio water (line 1)

            a₃: a- ratio steam (line 3)

            Index v: full-load

            with

            b= a_1v/ a_3v         and                                                                           (10)

            g1 = a1 / a1v         as well as                                                                (11)

            g₃= g₃/ a_3v                                                                                            (12)

            results in

            k_I/k_Iv = g₃(1+b) / (g₃/g₁+b)                                                                     (13)

The k - number ratio k_I / k_II can be formulated as follows.

            k_I/k_II = k_Iv/k_IIv k_I/k_Iv 1/(k_II/k_IIv)                                                                 (14)

With (10) and (11) follows

            k_Iv/k_IIv = (a1_IIv /a1_Iv) (1+b_II) / (1+b_I)                                                     (15)

The ratio of the a₁- numbers can be set to u1.

The following applies for the ratios k_I / k_IV and k_II / k_IIV

            k_I/k_Iv = g_1I(1+b_I) / (1+g_1I/ g_3Ib_I)                                                             (16)

            k_II/k_IIv = g_1II(1+b_II) / (1+g_1II/g_3IIb₂)                                                         (17)

With g1I »g1II (same medium) and g1II »g3II (single phase medium)

applies to

            k_I/k_II = (1+bII) / (1+bI) (1+bI) / (1+g1I/g3I bI)                                           (18)

The g- dependencies are taken from Rabek sources..

            g_1I= (m_1I/m_1vI)^0,8                                                                                   (19)

            g3I = (m_3I/m_3vI)^0,33                                                                                 (20)

With (18) to (20) the system can be solved completely.

 

3.  Calculation

Full load calculations (Load = 0, IFAL = 0) are based on the assumption of a Terminal Temperature Difference (which may be negative also), which is limited due to numerical reasons to -10 K. With assumption of this Terminal Temperature Difference all temperatures are calculated, A_II / A_I (5) as well as Q_II / Q_I are calculated. From the heat transfer relation (8) and the two balances for each fluids the mass flow m3 and kI x A can be determined.

For part load with given k_I·A  and m3 all temperatures are calculated. For this part load equations(15) as (18) - (20) are used.

The heat transfer area A_I (condenser) and A_II (super-heater) can be shifted with constant total area A dependent on the thermodynamic conditions..

 

4.  Application

To use the new model a control variable must be modified in the menu for definitions.

Part-load functions according to Rabek

 

1.  k-number - ratio

k/k₀ = (1/a₁₀+ 1/a₃₀) / (1/a₁+ 1/a₃) = (1 + (a₁₀/a₃₀)) / ((a₁₀/a₁) + (a₁₀/a₃₀) (a₃₀/a))

with

            a₁₀/a₃₀= b

            a₁/a₁₀= g₁   ;   a₃/a₃₀= g₃

 

k/k₀ = (1+b) / (1/g₁+ b/g₃)

k/k₀ = g₃(1 + b) / ((g₃/g₁) + b)                                                                          (21)

 

2.  Desuperheater/ Evaporator k-number

k_I/k_II = k_v/k_E = k_v0/k_E0  k_v/k_v0  1/(k_E/k_E0)

k_v0/k_E0 = (1/a_1E+ 1/a_3E) / (1/a_1v+ 1/a_3v) = a_1E/a_1v(1 + b_E) / (1 + b_v)                       (22)

(k_v/k_v0) (1/(k_E/k_E0) = g₁(1 + b_v) (1 + (g₁b_E/g₃)) / (1 + (g₁b_v/g₃)) g₁(1+b_E)

                                =  (1 + b_v) / (1 + (g₁b_v/g₃))                                                (23)

k_I/k_II = k_v/k_E = (1+b_E) / (1+b_v) (1+b_v) / (1+(g₁b_v/g₃))                                            (24)

 

3.  Typical values according to Rabek

g3 ~(m₃/m₀₃)^0,33    and   m₃/m₁ ~m₃₀/m₁₀

g₁ ~(m₁/m₀₁)^0,8

b_E~15

b_v~2

from (1)          k/k₀ = (m₃/m₃₀)^0,33   3/((m₃/m_v)^-0,5 + 2)                                                (25)

from (4)          k_I/k_II = k_v/k_E = 16/3 (1+2) / (1+ (m₃/m₃₀)^0,5  2)                                     (26)