

In simple cases, an optimization can be effected manually by varying the parameters or by means of an EbsScript. In more complex cases, particularly if there are multiple influencing variables, it is recommended to use the module EbsOptimize.
EbsOptimize offers two types of optimization algorithms:
EbsOptimize is activated via the menu command "Calculation" --> "Optimization". This command is only available if the corresponding flag is licensed. Then the optimizer dialog appears:
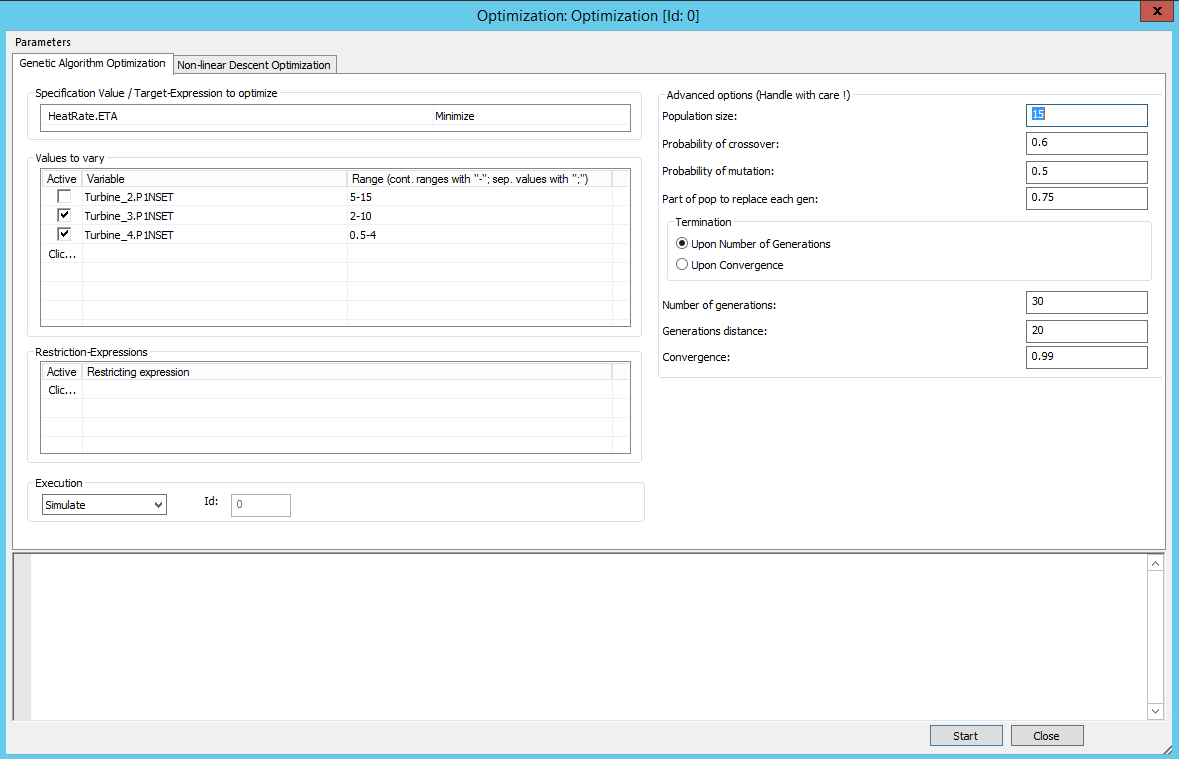
Regardless of the choice of optimization algorithm, the fundamental principle of the optimization in EBSILON®Professional can be described as follows: several specification values are selected as free parameters in an EBSILON model. A value range that the parameter may assume during the optimization calculation is specified for each of the free parameters. Furthermore, a target quantity is specified, which is to be optimized. This can be a simple result value or also a more complex mathematical expression.
Specification Value / Target Expression to optimize
Please click into the window for the optimization target. In the combo box, a simple result value can be selected as optimization target, or a more complex mathematical expression can be entered (in EbsScript syntax), which is to be minimized or maximized according to the setting on the right (combo box). In the example shown, the target is to minimize the heat rate.
Values to vary:
The variation parameters (influencing variables) can be selected after clicking on the button "Click to insert item", or any expression at will can be entered (in EbsScript syntax). The possible value range to be examined is to be entered for the selected variation parameters in each case.
Variation parameters can be edited with the context menu.
Restriction-Expression
In addition, restrictions can also be entered (in EbsScript syntax) in the case of boundary conditions ("Click to insert item"). The adherence to these boundary conditions is checked subsequent to each calculation run. Parameter sets which lead to a violation of the boundary conditions are discarded. It is advised to use these boundary conditions only for specifying restrictions for calculated values. Restrictions in the specification values should be entered in the value range of the variation parameters in order to avoid unnecessary calculations.
Button "Start"
Execution of the optimization calculation. Clicking the button "Start" activates the optimization calculation. Depending on the selected specifications, this calculation may take some time. The progress of the optimization calculation is displayed in the log shell.
Simulation / EbsScript
In an optimization calculation, usually multiple EBSILON simulations are executed. Alternatively, instead of simulations, it is also possible to execute an EbsScript with the specified ID in the individual EBSILON calculations. For instance, this may be useful if interim results emerge after a simulation that can be used in a second simulation.
EbsScript instead of simulation
If an EbsScript is executed instead of a simulation, the optimizer will expect a return value from the EbsScript. This allows the optimizer to evaluate whether the execution has been successful or not. The user has set this return value in the EbsScript with the command exit (return value). Here a return value of 0 is interpreted as a success, and any other number is interpreted as an error.
In the EbsScript at least one execution of the simulate function is expected to be done. The return code of the simulate function allows the user to set the return value of the EbsScript.
Example:
var src: CalculationResultEnum;
returncode: integer;
begin
src := simulate();
if (src >= calculationSuccessfulWithWarnings) then begin
returncode := -1;
end else begin
returncode := 0;
end;
exit (returncode);
end.
Log Output
In the output window (directly above the "Start" and "Close" buttons), log outputs are output during an optimization run, which allow the progress of the optimization calculation to be tracked. These outputs can also be output to a log file. See General Options-->Paths-->Optimizer Output-File
The optimization is based on an evolutionary (genetic) algorithm with a population size that remains constant (steady state). It is integrated in the calculation kernel of EBSILON®Professional. As this optimization method is probabilistic, each optimization run will have a different result. For numerous tasks in optimizing the operation, however, this does not pose a limitation. The crucial point is that the differences are on a small scale from the point of view of precision.
A value set (individual) consists of an assignment of values from the respective value range to the free parameters. A population, on the other hand, consists of a number of value sets. In one step, value sets are combined with each other (crossover); in addition, individual values of a value set can be changed easily (mutation). The selection procedure ensures that the best value sets will prevail.
The following parameters can be set for the sequence of the optimization according to the genetic algorithm:
Population size (usually 15)
To put it simply, the population size determines the range of an optimization. A population is generated arbitrarily. For instance, 20 output data sets are selected at random, from which their successors are also determined at random. The data set is changed slightly by means of mutation.
The higher the number of variables available, the bigger should be the population.
Probability of crossover (usually 0.6)
Crossover generally makes sense only in the case of more than one variable. It then takes into account the mutual influencing of several variables.
Probability of mutation (usually 0.5)
A Gaussian distribution is taken as the basis for the variation of individual value pairs. It can be damped with an increasing number of generations.
Part of population to replace each generation (usually 0.75)
This quantity determines which proportion (in %) of the best results is to be taken over for the following generation.
Criteria for termination
The optimization can be continued at will until the specified number of generations has been calculated or until the results coincide with the previous generation within the scope of the specified convergence range.
The second type of algorithms are non-linear descent methods. The procedure as well as the parameterization differ from the genetic algorithm. Due to the deterministic nature of the non-linear descent methods, these always yield the same results for the same input values, in contrast to the genetic algorithm.
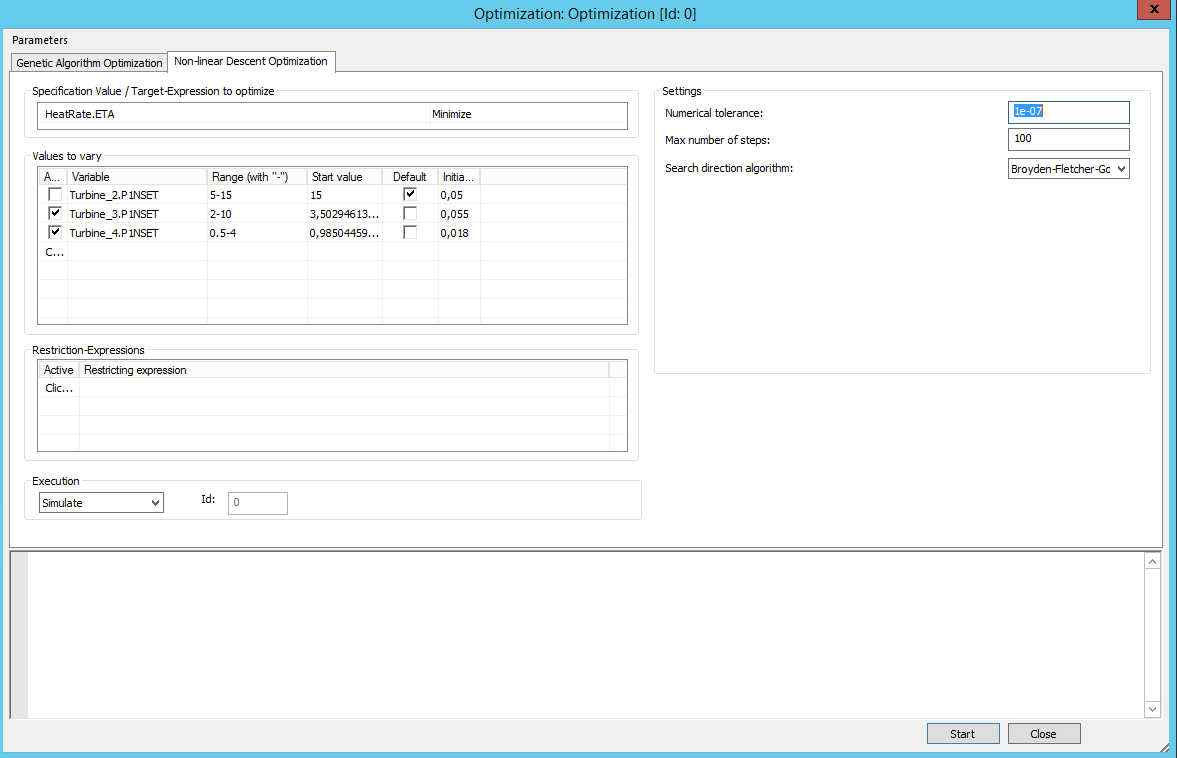
Start values
In the case of the descent methods, a start value within the scope of the parameters to be varied is required at all times. Beginning with this start value, the optimum is searched for step by step according to the respective algorithm. Obviously, the start value for the parameter must be within the correspondingly specified range of validity.
Initial increment
When searching for the optimum, in each step the respective partial derivatives of the target function are formed according to the parameters to be varied. As these derivatives can only be computed numerically, at least in the starting point for each parameter the value for the increment (parameter change for the calculation of the partial derivative) is required. The user can either manually specify this initial increment or rely on the default value. The default value is set depending on the specified range of validity of the respective parameter. In further steps, an automatic adjustment/refinement of the above-mentioned increments is performed by the optimizer depending on the behaviour of the target function.
Criteria for termination
The search for optimum is terminated when either the maximum number of steps is exceeded or the numerical tolerance is not reached. During the evaluation, the change of the objective function between the current and the previous optimization step is checked against the specified numerical tolerance.
In each step, the procedure calculates the derivative of the objective function according to all parameters. In the general case, this derivative is a vector: df/dx1, df/dx2, ..., df/dxn. Here is
The optimum is reached at a point where the derivative of the objective function is zero. Since numerically zero is not reached, the absolute value of the derivative - SQRT( df/dx1^2 + ... + df/dxn^2) - is checked against the specified numerical tolerance.
The tolerance is thus only used to decide whether the target function has a stationary point (df/dx=0).
Search direction algorithm
Various algorithms can be applied for the question in which direction the next step of the optimization calculation is made in the parameter space (or by how much which parameter value is modified). The most simple and most robust one here is the steepest descent method. With this method, the step is always made in the direction in which the target function changes the most. In spite of all advantages, this method has the lowest rate of convergence. Alternatively, the conjugate gradient method or two quasi-Newton methods:Davidon-Fletcher-Powell (DFP) or Broyden-Fletcher-Goldfarb-Shanno (BFGS) can be used. These methods have a better convergence behaviour. However, they were developed for the optimization tasks in which the parameters to be varied are not constrained in the scope (unconstrained optimization). Therefore these advanced algorithms have some difficulties when one or several parameters reach the limit of the range of validity during the optimization calculation. In contrast, the gradient descent is insensitive in its behaviour in such situations. Therefore also when choosing an advanced method (conjugate gradients, DFP, BFGS), the gradient descent is always used as a backup (should the method fail in an optimization step). The user will receive a corresponding warning in the log shell in the mentioned case.
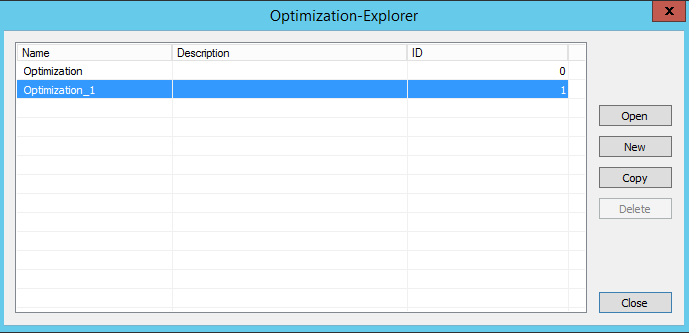
Similar to diagrams or EbsScript, several parameter sets within one EBSILON model (*.ebs file) are possible for the optimizer too. To save the existing parameter set or load a saved parameter set please click on the menu item “Parameters“ in the optimizer dialog. The optimizer parameter sets can be specified in an Optimization Explorer with name, description, and ID. The Optimization Explorer is started for each sub-item from the menu item “Parameters“ of the optimizer dialog.
EbsOptimize can also be activated from EbsScript.
An obsolete function "optimizeEasy" only initiates the optimization according to the genetic algorithm. Here the latest settings made in the EbsOptimize dialog are used. A modification of the settings from EbsScript is not possible.
Furthermore, there are two functions: "optimizeGA( {id:Integer}{, maxTimeInSeconds:Integer = 0} )" and "optimizeND( {id:Integer}{, maxTimeInSeconds:Integer = 0} )". In contrast to "optimizeEasy", these functions initiate the respective optimization algorithms (GA for genetic algorithm and ND for nonlinear descent methods) for the parameter set with the specified ID (Argument 1). Optionally, the runtime of the optimization calculation can be limited by Argument 2 of the function.