

In einfachen Fällen kann eine Optimierung durch Parametervariation manuell oder mit Hilfe eines EbsScripts durchgeführt werden. In komplexeren Fällen, insbesondere bei mehreren Einflussgrößen, bietet sich die Nutzung des Moduls EbsOptimize an.
EbsOptimize bietet 2 Arten von Optimierungsalgorithmen an:
Der Aufruf von EbsOptimize geschieht über den Menübefehl "Rechnen" --> "Optimierung". Dieser Befehl steht nur zur Verfügung, wenn das entsprechende Flag lizenziert ist. Es erscheint dann der Optimierer-Dialog:
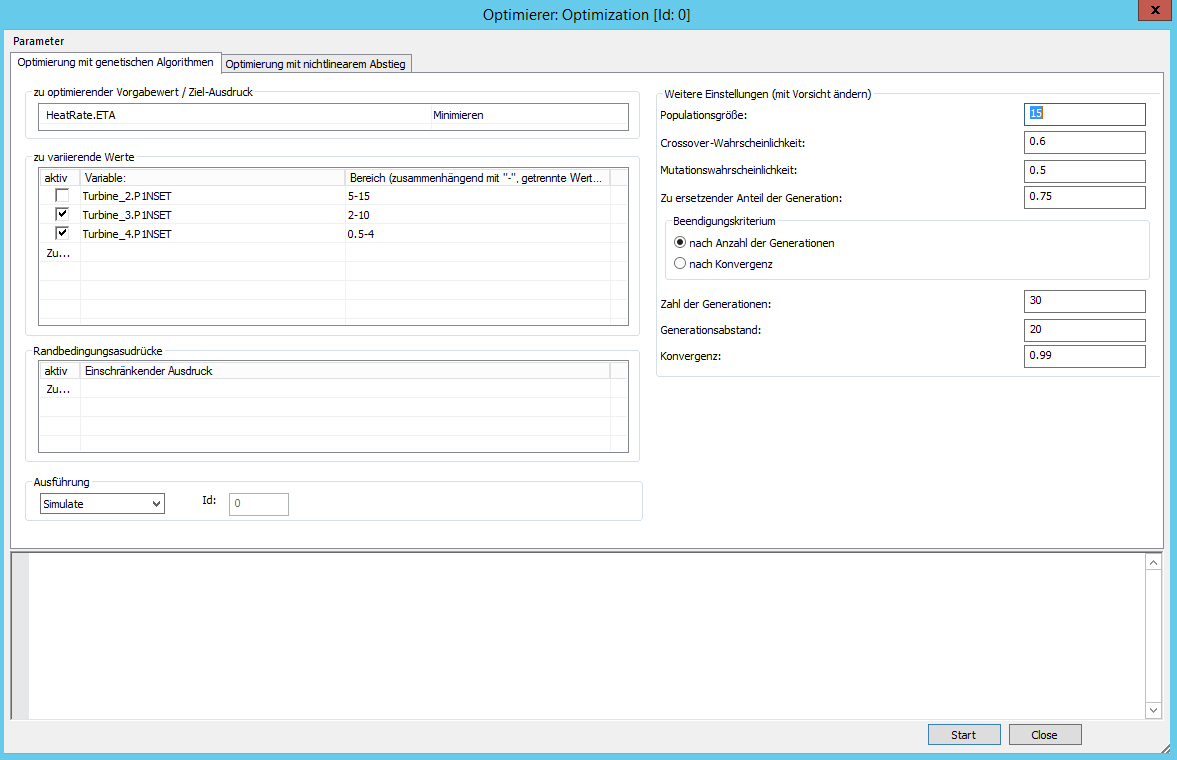
Unabhängig von der Wahl des Optimierungsalgorithmus lässt sich das Grundprinzip der Optimierung in EBSILON®Professional wie folgt beschreiben. In einem Ebsilon-Modell werden einige Spezifikationswerte als freie Parameter festgelegt. Zu jedem der freien Parameter wird ein Wertebereich angegeben, den der Parameter während der Optimierungsrechnung annehmen kann. Weiterhin wird eine Zielgröße angegeben, die optimiert werden soll. Dabei kann es sich um einen einfachen Ergebniswert handeln oder auch einen komplexeren mathematischen Ausdruck.
Zu optimierender Vorgabewert / Ziel-Ausdruck
Bitte in das Fenster Optimierungsziel klicken! In der Kombobox kann ein einfacher Ergebniswert als Optimierungsziel ausgewählt werden, bzw. kann ein komplexerer mathematischer Ausdruck (in EbsScript-Syntax) eingetragen werden, der entsprechend der Einstellung rechts (Kombobox) minimiert oder maximiert werden soll. Im dargestellten Beispiel ist das Ziel eine Minimierung des Wärmeverbrauchs.
Zu variierende Werte
Die Variationsparameter (Einflussgrößen) können nach Anklicken der Schaltfläche " Zum Einfügen bitte anklicken" ausgewählt werden, bzw. kann ein beliebiger Ausdruck (in EbsScript-Syntax) eingetragen werden. Für die ausgewählten Variationsparameter ist jeweils der mögliche Wertebereich einzutragen, der untersucht werden soll.
Variationsparameter können mit dem Kontextmenü bearbeitet werden.
Randbedingungsausdrücke
Zusätzlich können bei Randbedingungen noch Einschränkungen (in EbsScript-Syntax) eingegeben werden ("Zum Einfügen bitte anklicken") . Die Einhaltung dieser Randbedingungen wird im Anschluss an den einzelnen Rechenlauf geprüft. Parametersätze, die zu einer Verletzung der Randbedingungen führen, werden verworfen. Sinnvollerweise verwendet man diese Randbedingungen nur, um Einschränkungen bei berechneten Werten vorzugeben. Einschränkungen in den Vorgabewerten sollte man beim Wertebereich der Variationsparameter eintragen, um überflüssige Berechnungen zu vermeiden.
Knopf "Start"
Durchführung der Optimierungsrechnung. Durch Anklicken der Schaltfläche "Start" wird die Optimierungsrechnung angestoßen. Je nach Wahl der Vorgaben kann diese Berechnung längere Zeit in Anspruch nehmen. In der Log-Konsole wird der aktuelle Verlauf der Optimierungsrechnung angezeigt.
Simulation / EbsScript
Bei einer Optimierungsrechnung. werden normalerweise mehrere EBSILON Simulationen durchgeführt. Es besteht jedoch alternativ die Möglichkeit bei den einzelnen EBSILON-Rechnungen statt Simulation ein EbsScript mit der vorgegebenen Id auszuführen. Das kann z.B. nützlich sein, wenn nach einer Simulation Zwischenergebnisse entstehen, die in einer zweiten Simulation verwendet werden können. Ein solches EbsScript muss also mindestens einen simulate()-Aufruf enthalten. Der Rückgabewert des simulate()-Aufrufs muss für die Ermittlung des Exit-Codes genutzt werden.
EbsScript statt Simulation
Wenn statt Simulation ein EbsScript ausgeführt wird, erwartet der Optimierer vom EbsScript einen Rückgabewert. Damit beurteilt der Optimierer, ob die Ausführung erfolgreich war oder nicht. Diesen Rückgabewert muss im EbsScript mit dem Befehlsaufruf exit (Rückgabewert) gesetzt werden. Dabei wird ein Rückgabewert von 0 als Erfolg und jede andere Zahl als Fehler interpretiert.
Im EbsScript wird mindestens eine Ausführung der simulate-Funktion erwartet. Mit dem Rückgabewert der simulate-Funktion kann der Anwender den Rückgabewert des EbsScripts festlegen.
Beispiel:
var src:CalculationResultEnum;
returncode:integer;
begin
src := simulate();
if (src >= calculationSuccessfulWithWarnings) then begin
returncode := -1;
end else begin
returncode := 0;
end; exit (returncode);
end.
Logausgaben
Im Ausgabefenster (direkt über den Buttons "Start" und "Close") werden während eines Optimierungslaufs Logausgaben ausgegeben, die es erlauben, den Fortschritt der Optimierungsrechnung zu verfolgen. Diese Ausgaben können auch in eine Logdatei ausgegeben werden. Siehe dazu Allgemeine Einstellungen-->Pfade-->Optimierer-Ausgabedatei
Die Optimierung basiert auf einem evolutionären (genetischen) Algorithmus mit konstant bleibender Populationsgröße (steady state). Er ist im Rechenkern von EBSILON®Professional integriert. Da dieses Optimierungsverfahren probabilistisch ist, kommt jeder Optimierungslauf zu einem anderen Ergebnis. Für zahlreiche Aufgaben in der Betriebsoptimierung ist dieses jedoch keine Einschränkung. Entscheidend ist es, dass die Unterschiede in der aus der Genauigkeitssicht kleinen Größenordnung liegen.
Ein Wertesatz (Individuum) besteht aus einer Belegung der freien Parameter mit Werten aus dem jeweiligen Wertebereich. Eine Population wiederum aus einer Anzahl von Wertesätzen. In einem Schritt werden Wertesätze miteinander kombiniert (Cross-Over), zusätzlich können einzelne Werte eines Wertesatzes leicht geändert werden (Mutation). Durch Selektionsdruck wird sichergestellt, dass sich die besten Wertesätze durchsetzen.
Als Parameter für den Ablauf der Optimierung nach dem genetischen Algorithmus können eingestellt werden:
Populationsgröße (üblich 15)
Die Populationsgröße bestimmt, vereinfacht ausgedrückt, die Weite einer Optimierung. Eine Population wird zufällig erzeugt. Zum Beispiel werden 20 Ausgangsdatensätze zufällig gewählt, aus denen ebenfalls zufällig die Nachkommen erzeugt werden. Mittels Mutation wird der Datensatz leicht geändert.
Die Population sollte umso größer sein, je mehr Variablen vorhanden sind.
Crossover-Wahrscheinlichkeit (üblich 0.6)
Crossover ist generell nur bei mehr als einer Variablen sinnvoll. Es berücksichtigt dann die gegenseitige Beeinflussung von mehreren Variablen.
Mutationswahrscheinlichkeit (üblich 0.5)
Für die Variation einzelner Wertepaare wird eine Gaußverteilung zugrundegelegt. Diese kann mit zunehmender Generationszahl gedämpft werden.
Zu ersetzender Anteil der Generation (üblich 0.75)
Diese Größe bestimmt welcher Anteil (in %) von den besten Ergebnissen für die nächste Generation übernommen werden.
Beendigungskriterium
Die Optimierung kann wahlweise so lange durchgeführt werden, bis eine vorgegebene Zahl der Generationen durchgerechnet wurde oder bis die Ergebnisse im Vergleich zur vorherigen Generation im Rahmen des vorgegebenen Konvergenzbereichs übereinstimmen.
Bei der zweiten Art von Algorithmen handelt es sich um nichtlineare Abstiegsverfahren. Die Vorgehensweise sowie die Parametrierung unterscheidet sich dabei vom genetischen Algorithmus. Aufgrund der deterministischen Natur der nichtlinearen Abstiegsverfahren liefern diese, im Gegensatz zum genetischen Algorithmus, immer die gleichen Ergebnisse für die gleichen Eingabewerte.
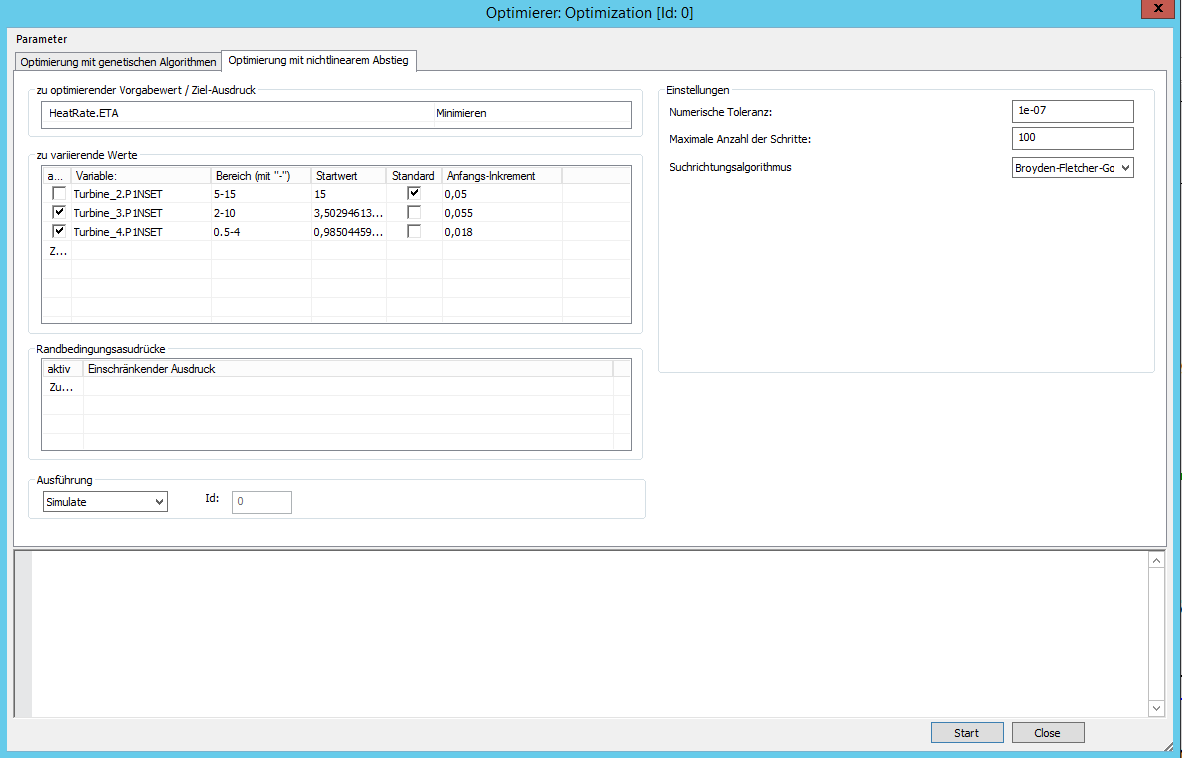
Startwerte
Bei den Abstiegsverfahren wird immer ein Startwert im Raum der zu variierenden Parameter benötigt. Ausgehend von diesem Startwert wird nach dem entsprechenden Algorithmus Schritt für Schritt das Optimum gesucht. Sinngemäß muss der Startwert für den Parameter in dem entsprechend angegebenen Gültigkeitsbereich liegen.
Anfangs-Inkrement
Auf der Suche nach Optimum werden bei jedem Schritt die jeweilige Partialableitungen der Zielfunktion nach den zu variierenden Parametern gebildet. Da diese Ableitungen nur numerisch gebildet werden können, wird zumindest im Startpunkt für jeden Parameter der Wert für den Inkrement (Parameteränderung für die Berechnung der Partialableitung) benötigt. Diesen Anfangs-Inkrement kann der Benutzer entweder manuell angeben oder sich auf den Standard-Wert verlassen. Der Standard-Wert wird in Abhängigkeit vom angegebenen Gültigkeitsbereichs des jeweiligen Parameter gebildet. Bei weiteren Schritten erfolgt eine automatische Anpassung / Verfeinerung der genannten Inkremente vom Optimierer abhängig vom Verhalten der Zielfunktion.
Beendigungskriterium
Die Suche nach Optimum wird beendet, wenn entweder die maximale Anzahl der Schritte überschritten oder die numerische Toleranz unterschritten wird. Bei der Auswertung wird die Änderung der Zielfunktion zwischen dem aktuellen und dem vorherigen Optimierungsschritt gegen die angegebene numerische Toleranz geprüft.
Das Verfahren rechnet in jedem Schritt die Ableitung der Zielfunktion nach allen Parametern. Diese Ableitung ist im Allgemeinfall ein Vektor: df/dx1, df/dx2, ..., df/dxn. Dabei ist
Das Optimum wird erreicht in einem Punkt, wo die Ableitung der Zielfunktion Null ist. Da numerisch Null nicht erreicht wird, wird der Absolutwert der Ableitung - SQRT( df/dx1^2 + ... + df/dxn^2) - gegen die angegebene numerische Toleranz geprüft.
Die Toleranz wird also nur benutzt, um zu entscheiden, ob die Zielfunktion einen stationären Punkt hat (df/dx=0).
Algorithmus für die Richtungssuche
Bei der Frage in welcher Richtung im Parameterraum der nächste Schritt der Optimierungsrechnung erfolgt (oder um wie viel welcher Parameterwert verändert wird), können verschiedene Algorithmen eingesetzt werden. Der einfachste und robusteste dabei ist das Verfahren der steilsten Gradienten. Bei diesem Verfahren wird der Schritt immer in die Richtung getan, in der sich die Zielfunktion am stärksten ändert. Trotz aller Vorteile hat dieses Verfahren die niedrigste Konvergenzrate. Alternativ kann das Verfahren der konjugierten Gradienten oder 2 Quasi-Newton-Verfahren: Davidon-Fletcher-Powell (DFP) oder Broyden-Fletcher-Goldfarb-Shanno (BFGS) eingesetzt. werden. Diese Verfahren haben ein besseres Konvergenzverhalten. Jedoch wurden sie für die Optimierungsaufgaben entwickelt, in denen die zu variierenden Parameter im Raum nicht begrenzt sind (zu engl. unconstrained optimization). Daher haben diese fortgeschrittenen Algorithmen ihre Schwierigkeiten, wenn ein oder mehrere Parameter während der Optimierungsrechnung an Rand des Gültigkeitsbereichs kommen. Dagegen verhält sich das Verfahren der steilsten Gradienten in solchen Situationen unempfindlich. Deswegen wird auch bei der Wahl eines fortgeschrittenen Verfahrens (konjugierte Gradienten, DFP, BFGS) immer als Sicherung (für den Fall des Scheiterns des Verfahrens bei einem Optimierungsschritt) das Verfahren der steilsten Gradienten verwendet. Der Benutzer wird diesbezüglich in der Log-Konsole gewarnt.
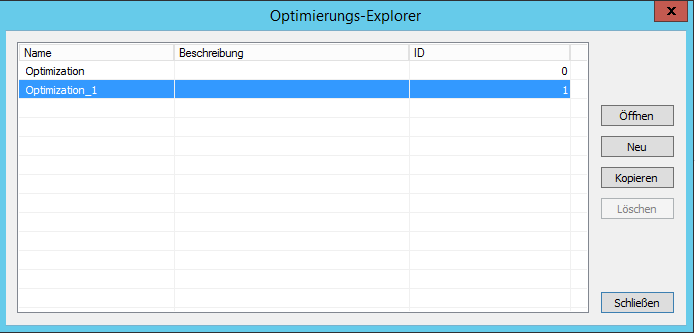
Wie bei Diagrammen oder EbsScript sind auch für den Optimierer mehrere Parametersätze innerhalb eines EBSILON Modells (*.ebs-Datei) möglich. Um den bestehenden Parametersatz zu speichern oder einen gespeicherten Parametersatz zu laden, klicken Sie bitte auf den Menü-Punkt "Parameter" im Optimierer-Dialog. Die Optimierer-Parametersätze können in einem Optimierungs-Explorer mit Namen, Beschreibung und ID spezifiziert werden. Der Optimierungs-Explorer wird gestartet beim Aufruf jedes Menü-Punktes "Parameter" des Optimierer-Dialogs.
EbsOptimize kann auch aus EbsScript aufgerufen werden.
Eine veraltete Funktion "optimizeEasy" stößt die Optimierungsrechnung nur nach genetischem Algorithmus an. Hierbei werden die zuletzt im EbsOptimize-Dialog vorgenommenen Einstellungen verwendet. Eine Änderung der Einstellungen aus EbsScript ist nicht möglich.
Weiterhin gibt es 2 Funktionen: "optimizeGA( {id:Integer}{, maxTimeInSeconds:Integer = 0} )" und "optimizeND( {id:Integer}{, maxTimeInSeconds:Integer = 0} )". Im Gegensatz zu "optimizeEasy" stoßen diese Funktionen die jeweilige Optimierungsalgorithmen an (GA für genetischen Algorithmus und ND für nichtlineare Abstiegsverfahren) für den Parametersatz mit der spezifizierten ID (Argument 1). Optional kann die Laufzeit der Optimierungsrechnung durch das Argument 2 der Funktion begrenzt werden.