基于 VDI 2048 形式化处理 Ebsilon 中的不等式

 

除了物理方程辅助条件（约束）外，在最小化误差平方和时还必须考虑不等式。例如，效率或蒸汽质量份数必须要小于 1。

这种不等式约束条件可以整合到方程（18）的迭代方案中，用于解决由方程（1）,（2）定义的最小值问题。

这里观察到，如果不等式 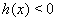 成立，则存在 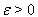，所以 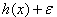= 0。通过引入松弛变量 y 作为辅助变量，不等式可以在形式化的框架内通过以下方式表示，即在辅助变量的定义方程的背景下，不等式可以通过方程  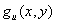的附加辅助条件来表示：

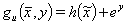 (27)

或

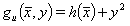 (28)

项 y² 和 ey 总是正的，所以只有在满足不等式约束条件 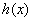 时，方程辅助（约束）条件  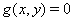才能得到满足。

由于 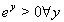，方程（27）严格执行 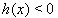，而对于 y=0 ，方程（28）也允许 h(x) = 0，，即正好是边界上的解。

 

迭代形式化假定辅助变量的定义方程是可逆的。由于

  

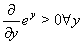
方程（27）与所述形式化无缝契合。这里方程（27）对应于 VDI 2048，表 2中的方程（39）。在根据方程（18）制定迭代程序时，不需要引入用于切换辅助条件（打开/关闭）的捕获范围。

方程式类型的约束条件。(28）违反了边界处的可逆性（仅），但可以通过算法中的案例区分来考虑到。例如，首先搜索允许范围内的最小值，约束条件为y>0，在第二步中用约束条件 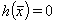 代替 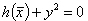，搜索边界上的最小值。最小的一个就是所需的解。