
EBSILON®Professional Online Documentation

在辅助(约束)条件(2)(见"问题的数学表述")下寻找最小值(1)的解,是相应拉格朗日函数 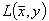 梯度消失的点。
梯度消失的点。
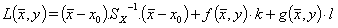 (3)
(3)
这里 k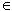
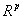 ,
, 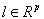 是所谓的拉格朗日乘数。在拉格朗日表述的背景下,这些都是根据局部最小值的存在条件,以及修正的估计值和辅助量共同来确定的:
是所谓的拉格朗日乘数。在拉格朗日表述的背景下,这些都是根据局部最小值的存在条件,以及修正的估计值和辅助量共同来确定的:
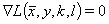
生成以下方程:
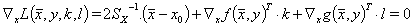 (4)
(4)
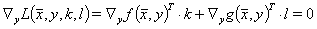 (5)
(5)
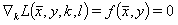 (6)
(6)
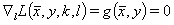 (7)
(7)
方程(4-7)代表了一个非线性方程组,用于估计值 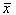 ,相应的辅助量 y 和拉格朗日乘数 k, l。通过线性化方程组,可以推导出一个迭代规则来改进原始值,以最终获得满足辅助(约束)条件的估计值。这种方法与 VDI 2048 提出的方法相一致。
,相应的辅助量 y 和拉格朗日乘数 k, l。通过线性化方程组,可以推导出一个迭代规则来改进原始值,以最终获得满足辅助(约束)条件的估计值。这种方法与 VDI 2048 提出的方法相一致。