原始数据分析和以平衡形式表示的辅助（约束）条件

 

在这里描述的方法中实施原始数据分析需要特别讨论。由于原始数据分析不是基于修正后的估计值，属于原始数据的辅助变量的值并不是预先知道的，必须进行确定。此外，必须考虑到辅助（约束）变量对违反辅助（约束）条件的置信区间的影响。

为了确定与原始数据 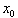 相关的辅助量 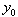，我们注意到，根据假设，p 个辅助量由 p 个方程  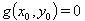定义。由于方程 g 通常是非线性的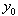， 必须在牛顿迭代的背景下确定，以计算零点：

设 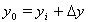。然后，线性化得到 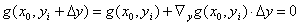。假设函数矩阵  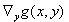在有解的情况下是可逆的，这就产生了用于确定与原始数据  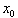相关的辅助量  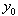的迭代规则：

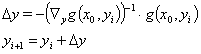 (23)

当迭代完成后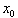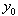，, 就是已知的。然后代入到 r 的物理辅助（约束）条件 f(x,y)，将产生原始数据分析对约束条件  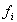的违反情况 

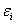
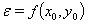                                (24)

在原始数据分析中，不仅要指定辅助（约束）条件的违反情况，而且还要分别指定其置信区间与方差。这些都是在计算辅助（约束）条件的误差时确定的，如同 VDI 2048，表 2，方程(61)中指定的那样：

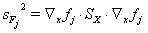
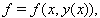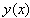正如在关于计算校正的协方差的段落中已经讨论过的一样，这里必须考虑  其中 由方程 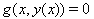 定义。因此，公式（21），(22）再次适用，所以在这里选择的公式的背景下，方程

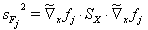                      (25)

将被使用，这里与方程（10）类似，定义方程

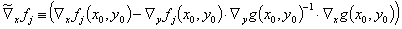                 (26)