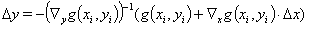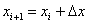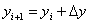为了推导迭代程序,线性化方程(4-7)。由于误差平方和的双线性结构和以及假定辅助变量 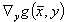 定义方程的导数矩阵可逆,可以从产生的方程中消除拉格朗日乘数。因此,迭代只发生在估计值的改进和辅助变量中。这也与 VDI 2048 中建议的方法一致。
定义方程的导数矩阵可逆,可以从产生的方程中消除拉格朗日乘数。因此,迭代只发生在估计值的改进和辅助变量中。这也与 VDI 2048 中建议的方法一致。
这最终是经典牛顿方法的一个变体,用于约束条件下进行数值最小化。
为了线性化方程(4-7),确定 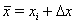 ,
, 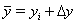 ,其中
,其中 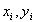 是第 i 个迭代步骤中的值。在最低阶中,将产生以下结果:
是第 i 个迭代步骤中的值。在最低阶中,将产生以下结果:
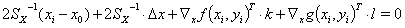 (4a)
(4a)
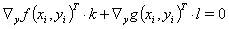 (5a)
(5a)
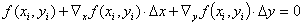 (6a)
(6a)
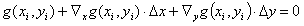 (7a)
(7a)
由于辅助变量的定义方程的可逆性,从方程(5a)中得到拉格朗日乘数之间的关联性
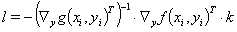 (8)
(8)
可以将结果(8)带入方程(4a)中,产生以下结果:
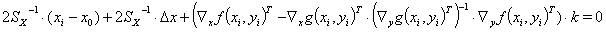 (9)
(9)
或者,由于 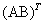 =
= 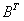
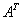 ,
, 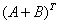 =
= 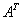 +
+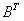 ,
, 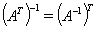
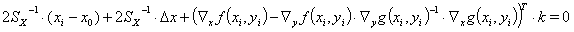 (9a)
(9a)
为了简化符号,这里的转换函数矩阵 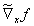 应定义为
应定义为
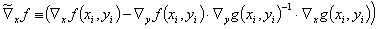 (10)
(10)
然后方程(9a)变成
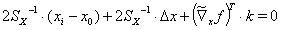 (11)
(11)
应该注意的是,对于带 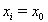 的第一个迭代步骤,方程(10)对应于 VDI 2048,表 1,方程(115),对导数矩阵进行了转换,以消除辅助变量。
的第一个迭代步骤,方程(10)对应于 VDI 2048,表 1,方程(115),对导数矩阵进行了转换,以消除辅助变量。
从方程(7a)可以看出,由于辅助变量定义方程的可逆性,辅助变量的修正改进可以通过测量值的修正来确定:
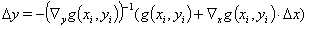 (12)
(12)
将方程(12)带入方程(6a),得到
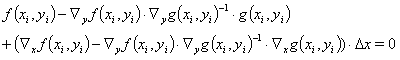 (12a)
(12a)
带入已经引入的转换函数矩阵 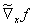 和相应定义的转换矛盾向量
和相应定义的转换矛盾向量
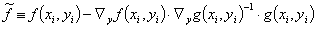 (13)
(13)
方程(12a)变成
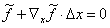 (14)
(14)
经过经过转换消除辅助变量后,方程(14)对应于 VDI 2048,表 1 中的方程(112)。可以从方程(11)和(14)中消除拉格朗日乘数 k,以定义准则中提出的修正 ∆X。
方程(11)的结果为
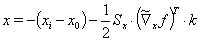 (15)
(15)
将方程(15)带入方程(14),确定拉格朗日乘数 k
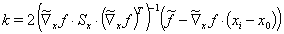 (16)
(16)
方程(16)可以再次用于方程(15),以最终确定修正 Dx:
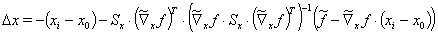 (17)
(17)
对于带 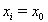 的第一个迭代步骤,这正好对应 VDI 2048,表 1,方程(120)给出的修正改进。如果没有方程(17)中对附加项
的第一个迭代步骤,这正好对应 VDI 2048,表 1,方程(120)给出的修正改进。如果没有方程(17)中对附加项 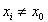 ,,这里描述的迭代程序将得到满足辅助(约束)条件的解,但不一定是误差平方和的最小值。这在附录 6.3 中用一个简单的例子说明。附加项确保能收敛到误差平方和的(局部)最小值。
,,这里描述的迭代程序将得到满足辅助(约束)条件的解,但不一定是误差平方和的最小值。这在附录 6.3 中用一个简单的例子说明。附加项确保能收敛到误差平方和的(局部)最小值。
综上所述,根据 VDI 2048 在辅助(约束)条件下最小化误差平方和,同时考虑到 Ebsilon 中应用的辅助(约束)变量,迭代程序由方程(10,13,17,12)给出:
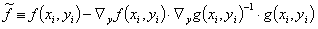
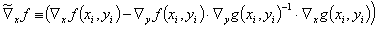
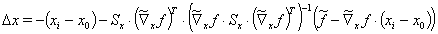 (18)
(18)