---

统计学基本术语

以下必须适用于随机变量 x 的分布函数：

 

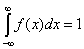                                                                                           (1)

 

x 的期望值被定义为

 

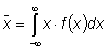                                                                                      (2)

 

以及方差为

 

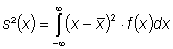                                                                      (3)

 

标准偏差由平方根产生
 

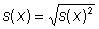                                                                                         (4)

 

如果不知道概率密度，可以从样本中获得均值和方差的期望真实估计

 

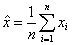                                                                                                   (5)

 

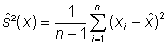                                                                           (6)

 

两个随机变量 x 和 y 之间存在随机独立性，如果

 

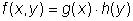                                                                                    (7)

 

是有效的。

 

这意味着 x 和 y 的共同概率密度等于单个概率密度的乘积。协方差可以理解为

 

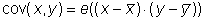                                                                   (8)

 

算子 e 代表了方程 （2） 意义上的期望值形成。协方差是衡量 x 和 y 的相互依赖性的度量，一个派生量是相关性系数。

 

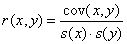                                                                                      (9)

 

可以证明，以下内容始终有效：

 

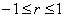                                                                                                   (10)

           

对于线性相关，适用

 

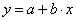                                                                                                 (11)

 

   

当 b 为正时：                      r(x,y) = 1

当 b 为负时：                      r(x,y) = -1

 

如果变量之间是相互独立的 ，则

 

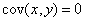
对于许多随机变量，建议使用矩阵符号来表示：

 

变量向量                                           转置的变量向量

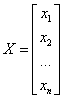
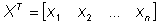                                                           (12)

 

协方差矩阵：

 

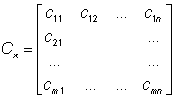                                                                          (13)

 

 

对角线元素是方差

 

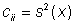                                                                                                   (14)

 

此外，对称性成立

 

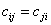                                                                                                         (15)

 

如果 E 表示构建预期值的算子，那么可以写成：

 

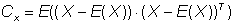                                                           (16)

 

误差传播规律源于以下观察结果。矢量 Y 是由 X 通过线性变换产生的

 

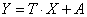                                                                                                (17)

 

以下内容适用于 Y 的预期值和协方差：

 

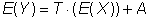                                                                                (18)

 

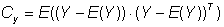                                                              (19)

 

有了 (17) 和 (18)，就得到：

 

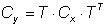                                                                                           (20)

 

假设预期值 E(X) 附近的 yi 可以用线性方式表示，可以得到以下结果

 

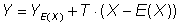                                                                         (21)

 

其中

 

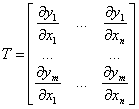                                                                                   (22)

 

如果将方程（22）代入方程（20），就可以得到误差传播规律。如果 x 是相互独立的，那么 Cx 只包含对角线元素，对于 yi 的方差来说，遵循

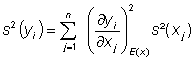                                                                   (23)

 

正态分布总体方差估计值的分布：

变量

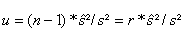                                                                      (24)

 

遵循自由度为 r 的 CHI^2 分布，预期值为

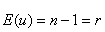                                                                                          (25)

 

以及

方差

 

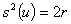                                                                                                 (26)

变量

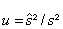                                                                                                   (27)

 

遵循一个特殊的 F 分布（有两个参数的费雪（Fisher）分布：自由度 r，无穷大），预期值为

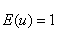                                                                                                    (28)

 

以及

方差

 

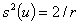                                                                                               (29)

 

如果将计算出的相对均方误差与分布函数的 95% 分位数联系起来，就可以得到一个拟合因子的评价标准，这个标准可以称为 CHI^2 -检测比率。

 

CHI^2 -检测比               <= 1 拟合度可靠性高

                                       >  1 测量数据的不一致性太高