Treatment of inequalities in Ebsilon in the context of the VDI 2048 formalism

 

In addition to the physical auxiliary conditions of the equations, also inequalities are to be considered when minimizing the error sum of squares. These result e.g. from the requirement that efficiencies or steam mass fractions are to be less than 1.

Such inequality auxiliary conditions can be integrated into the iteration scheme in equation (18) for the minimum value problem defined by equations (1,2).

 

Here we observe that if the inequality 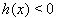applies, a 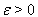exists, so that 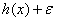= 0. By introducing a slack variable y as auxiliary variable, inequalities can thus be represented in the context of our formalism by means of additional auxiliary conditions of the equations 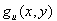in the context of the definition equations of the auxiliary variables:

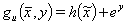 (27)

or

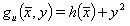 (28)

The terms y²  and e^y, respectively, are always positive, so that the auxiliary conditions of the equations 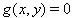 can only be achieved if the inequality conditions for 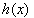are complied with.

Due to 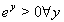, equation (27) strictly enforces 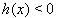, while for  y=0 equation (28) also allows h(x) = 0, i.e. solutions exactly on the boundary.

 

The iteration formalism assumes the invertibility of the definition equations of the auxiliary variables. Due to  

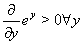  equation (27) integrates seamlessly into the described formalism. Here equation (27) corresponds to equation (39) in VDI 2048, Sheet 2. The introduction of snap ranges for switching the auxiliary conditions on and off is not required in the case of a formulation of the iteration procedure according to equation (18).

Auxiliary conditions of the type of equation (28) violate the invertibility (only) at the boundary, but can be considered in the algorithm by means of case-by-case analysis. E.g. by means of the restriction y > 0 you first search for minima within the feasible range and in a second step with the auxiliary condition 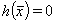instead of 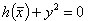you search for minima on the boundary. The least one is the desired solution.