The mathematical formulation of the problem

 

VDI 2048 carries out a Gaussian computation of adjustment. For this, a corrected data record of estimated values 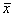is defined to a set of raw data 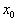in such a way that the error sum of squares calculated with the empirical covariance matrix 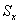becomes minimal;

           (1)

Here are 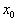,  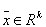. For the minimization, the laws of physics the measured values have to conform to are to be complied with as auxiliary conditions. Here these auxiliary conditions shall be formulated in the form

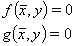                                      (2)

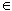
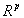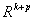
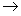
y  is a vector of auxiliary variables, the  p equations g: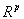are the definition equations of the auxiliary variables, and the equations f: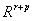0 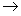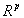are the r physical auxiliary conditions that have been defined by means of the p auxiliary variables.

As the equations g are to be the definition equations of the auxiliary variables, we assume that the equations 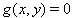 can be solved to y , i.e. that the p x p derivative matrix

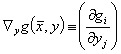
in an environment of the solution (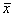,y) is invertible by  g(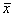,y)=0 .

The auxiliary variables do not directly enter into the calculation of the error sum of squares in equation (1). They are defined by the definition equations of the auxiliary quantities. Accordingly, no empirical covariances are specified for the auxiliary quantities but, as described in VDI 2048, covariances are calculated in the context of an error propagation from the empirical covariances of the raw data and the estimated values, respectively.