

The solutions of the search for the minimum (1) under the auxiliary conditions (2) (see “The mathematical formulation of the problem“) are the points where the gradient of the corresponding Lagrange function 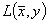 disappears:
disappears:
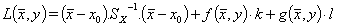 (3)
(3)
Here k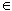
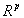 ,
,  are the so-called Lagrange multipliers. In the context of the Lagrange formalism, these are defined from the condition for the existence of a local minimum, together with the corrected estimated values and the auxiliary quantities:
are the so-called Lagrange multipliers. In the context of the Lagrange formalism, these are defined from the condition for the existence of a local minimum, together with the corrected estimated values and the auxiliary quantities:
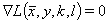
The following equations arise:
 (4)
(4)
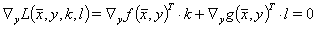 (5)
(5)
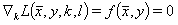 (6)
(6)
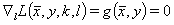 (7)
(7)
The equations (4 - 7) represent a non-linear equation system for the estimated values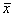 , the corresponding auxiliary quantities y as well as the Lagrange multipliers k, l. By means of a linearization it is possible to derive an iteration rule for the corrections of the raw data to finally receive the estimated values that comply with the auxiliary conditions. This approach is consistent with the procedure suggested by VDI 2048.
, the corresponding auxiliary quantities y as well as the Lagrange multipliers k, l. By means of a linearization it is possible to derive an iteration rule for the corrections of the raw data to finally receive the estimated values that comply with the auxiliary conditions. This approach is consistent with the procedure suggested by VDI 2048.