EBSILON®Professional Online Documentation
The execution of the raw data analysis in the context of the procedure described here requires special discussion. As the raw data analysis does not start with the corrected estimated values, the values of the auxiliary quantities that belong to the raw data are not known beforehand and have to be determined. Moreover, the influence of the auxiliary quantities on the confidence intervals of the violations of the auxiliary conditions is to be considered.
Concerning the definition of the auxiliary quantities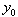 
that are attributed to the raw data 
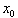, we remark that the p auxiliary quantities are defined by the p equations 
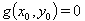according to our assumptions. As the equations g will usually be non-linear, the 
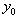will have to be determined in the context of a Newton iteration for calculating the zeroes:
Let be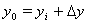 
. Then the linearization results in 
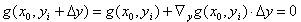. With the assumed invertibility of the functional matrix 
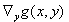in an environment of the solution of interest, this results in the iteration rule for determining the auxiliary quantities 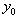attributed to the raw data :
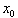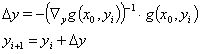(23)
When the iteration is finished, the 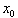, 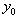are known. Inserting into the r physical auxiliary conditions f(x,y) will then yield the violations 
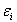of the auxiliary conditions 
for the raw data analysis
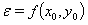(24)
In the context of the raw data analysis, not only the violations of the auxiliary conditions are to be specified, but also their confidence intervals and variances, respectively. These are to be determined in the context of a calculation of errors for the auxiliary conditions, as specified e.g. in VDI 2048 Sheet 2 equation (61):
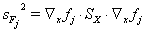
As already discussed in the paragraph on the calculation of the covariances of the corrections, it has to be considered here that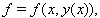 
wherein 
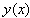is defined by the equations 
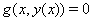. Thus equations (21,22) apply again, so that in the context of the formulation chosen here
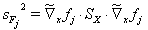(25)
is to be used, wherein similar to equation (10)
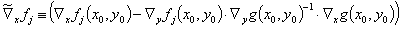(26)
is defined.