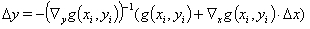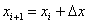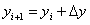The equations (4 - 7) are linearized for deriving an iteration procedure. Due to the bilinear structure of the error sum of squares and the assumed invertibility of the derivative matrix of the definition equations of the auxiliary variables 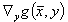 , the Lagrange multipliers can be eliminated from the arising equations. Thus the iteration occurs only in the corrections of the estimated values and in the auxiliary quantities. This again is consistent with the procedure suggested in VDI 2048.
, the Lagrange multipliers can be eliminated from the arising equations. Thus the iteration occurs only in the corrections of the estimated values and in the auxiliary quantities. This again is consistent with the procedure suggested in VDI 2048.
After all, this is a variant of the classical Newton procedure for numerical minimization under auxiliary conditions.
For the linearization of the equations (4 -7) we determine 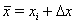 ,
, 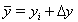 wherein
wherein 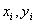 are the values in the i^th iteration step. In the lowest order, the following will result:
are the values in the i^th iteration step. In the lowest order, the following will result:
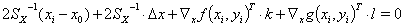 (4a)
(4a)
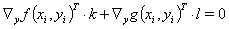 (5a)
(5a)
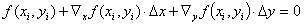 (6a)
(6a)
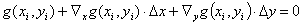 (7a)
(7a)
Due to the invertibility of the definition equations of the auxiliary variables, from equation (5a) we receive a correlation between the Lagrange multipliers
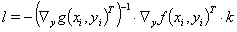 (8)
(8)
We can insert the result (8) in equation (4a) . So the following will result:
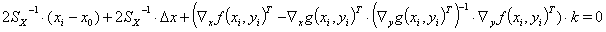 (9)
(9)
or due to 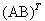 =
= 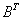
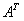 ,
, 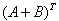 =
= 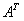 +
+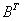 ,
, 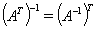
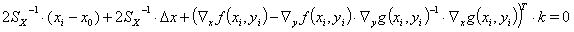 (9a)
(9a)
For simplifying the notation, here a transformed functional matrix 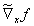 shall be defined by
shall be defined by
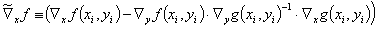 (10)
(10)
Then equation (9a) becomes
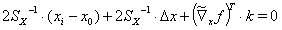 (11)
(11)
Please note that for the first iteration step with 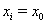 , equation (10) corresponds to equation (115) in VDI 2048, Sheet 1 with a derivative matrix transformed for eliminating the auxiliary variables.
, equation (10) corresponds to equation (115) in VDI 2048, Sheet 1 with a derivative matrix transformed for eliminating the auxiliary variables.
From equation (7a) again, the correction of the auxiliary variables can be determined from the correction of the measured values due to the invertibility of the definition equations of the auxiliary variables:
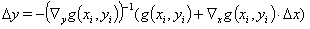 (12)
(12)
Inserting equation (12) into equation (6a) will result in
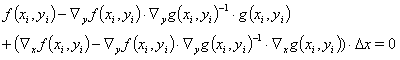 (12a)
(12a)
With the transformed functional matrix 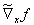 already introduced and an accordingly defined transformed vector of the contradictions
already introduced and an accordingly defined transformed vector of the contradictions
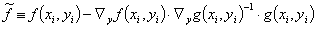 (13)
(13)
equation 12a becomes
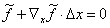 (14)
(14)
Equation (14) corresponds to equation (112) in VDI 2048 Sheet 1 after a transformation for eliminating the auxiliary variables. It is possible to eliminate the Lagrange multipliers k from the equations (11) and (14) to define the corrections ∆X as demonstrated in the guideline.
Equation (11) results in
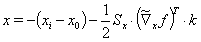 (15)
(15)
By inserting equation (15) into equation (14) the Lagrange multipliers k define themselves
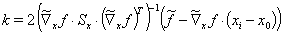 (16)
(16)
Equation (16) can again be used in equation (15) to finally determine the corrections Dx :
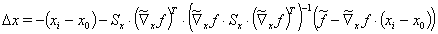 (17)
(17)
In the first iteration step with 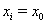 , this is precisely the correction specified in VDI 2048 Sheet 1 in equation (120). Without the terms additionally arising in equation (17) for
, this is precisely the correction specified in VDI 2048 Sheet 1 in equation (120). Without the terms additionally arising in equation (17) for 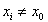 , the iteration procedure described here will lead to a result that complies with the auxiliary conditions, but not necessarily to the minimum of the error sum of squares. This is shown in Appendix 6.3 using a simple example. The additional terms ensure the convergence into a (local) minimum of the error sum of squares.
, the iteration procedure described here will lead to a result that complies with the auxiliary conditions, but not necessarily to the minimum of the error sum of squares. This is shown in Appendix 6.3 using a simple example. The additional terms ensure the convergence into a (local) minimum of the error sum of squares.
In summary, the iteration procedure according to VDI 2048 for minimizing the error sum of squares under auxiliary conditions and considering auxiliary variables implemented in Ebsilon is thus given by the equations (10, 13, 17, 12):
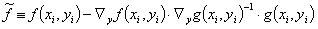
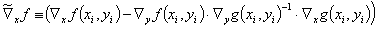
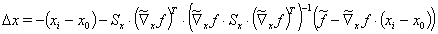 (18)
(18)