---

Fundamental terms of Statistics

The following must apply for the distribution function of a random variable x:

 

                                                                                           (1)

 

The expected value of x is defined as

 

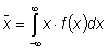                                                                                      (2)

 

and the variance as

 

                                                                      (3)

 

The standard deviation results from the square root
 

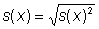                                                                                         (4)

 

If the probability densities are not known, then the unbiased estimation values for the mean value and the variance can be obtained from samples.

 

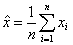                                                                                                   (5)

 

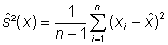                                                                           (6)

 

Stochastic independence exists between two random variables x and y, when

 

                                                                                    (7)

 

is valid.

 

This means that the common probability density of x and y is equal to the product of the individual probability densities. The covariance means

 

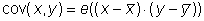                                                                   (8)

 

The operator e represents the expected value formation in the sense of equation (2). The covariance is a measure of the mutual dependency of x and y. A derived quantity is the correlation coefficient.

 

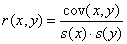                                                                                      (9)

 

It can be shown that the following is always valid:

 

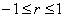                                                                                                   (10)

           

For a linear relationship          

 

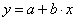                                                                                                 (11)

 

is valid:

when b is positive:                      r(x,y) = 1

when b is negative :                    r(x,y) = -1

 

If the variables are independent of each other, then

 

 

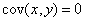
The matrix notation is recommended for may random variables:

 

Variable vector                                Transposed variable vector

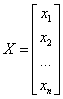
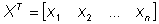                                                           (12)

 

Covariance matrix:

 

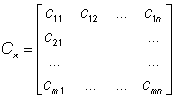                                                                          (13)

 

 

The diagonal elements are the variances

 

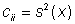                                                                                                   (14)

 

Further, this symmetry is also valid

 

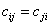                                                                                                         (15)

 

If E denotes the operator for the expected value building, then it can be written:

 

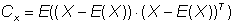                                                           (16)

 

The error propagation law arises from the following observation. The vector Y results from X through the linear transformation

 

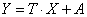                                                                                                (17)

 

The following applies to expected value and covariance:

 

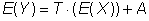                                                                                (18)

 

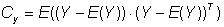                                                              (19)

 

With (17) and (18), it follows:

 

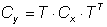                                                                                           (20)

 

Under the assumption, that the y_i can be displayed linearly around the expected value E(X) linear, it follows

 

                                                                         (21)

 

with

 

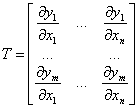                                                                                   (22)

 

If equation (22) is used in equation (20), then one reaches the error propagation law. If the x are independent of each other, then C_x contains only the diagonal elements, and it follows for the variances of y_i

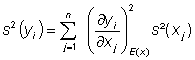                                                                   (23)

 

Distribution of the estimated value of the variance for a normal-distributed population:

The variable

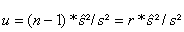                                                                      (24)

 

follows a CHI^2-distribution of the degree of freedom r with the expected value

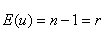                                                                                          (25)

 

and

the variance

 

                                                                                                 (26)

The variable

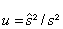                                                                                                   (27)

 

follows a special F-distribution (Fisher-distribution with two parameters: degree of freedom r and infinite) with the expected value

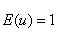                                                                                                    (28)

 

and

the variance

 

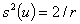                                                                                               (29)

 

If one refers the calculated relative mean square error to the 95 %-quantile of the distribution function, then one gets an evaluation criterion for the adaptation factor, which can be called as the CHI^2-test ratio.

 

CHI^2-test ratio   <= 1 Reliable adaptation

                                       >  1 too high contradictions in the measured data