Ensuring monotonic convergence

 

On Sheet 1, equation (145), VDI 2048 demands monotonic convergence as a quality criterion. This cannot be ensured beforehand by means of the iteration procedure. It cannot be ruled out that the calculated Newton step leads beyond the sought minimum. That would result in an oscillating, non-monotonic behaviour of the iteration. In order to prevent this and to ensure monotonic convergence, an automatic incrementation control is integrated into the algorithm.

For this, let  r(x,y) be the 2-standard of the violation of the auxiliary conditions:

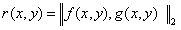       (29)

i.e. the length of the vector (f,g) in 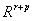. Thus in each iteration step, an incrementation control according to the “backtracking line search“ is carried out with two parameters

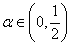 and 

1. Calculate D x,  Dy from xi, yi  according to equation 18

2. backtracking line search

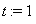
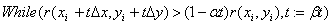
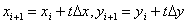
This procedure ensures the monotonic convergence of the iteration into a minimum of the error sum of squares complying with the auxiliary conditions.