

Measurement values can depend stochastically on one another. The covariance matrix is used to define the correlations between the measurement values. Correlation coefficients are used as input, which can take up values between -1 and +1. A positive value indicates that a change in a measurement value cause a change in another measurement value in the same direction. A negative value indicates: If one value decreases, the other value increases, or vice versa.
It is important to distinguish between three types of correlations:
Both the first two types of correlations must be specified (mostly programmed or modelled). The correlations resulting from the model are the result of the validation calculation.
Explicit correlations of measurement values must be taken into account only when their measurements are not independent of one another (e.g. the same measurement apparatus). These correlations can be overlaid on random deviations, so that the correlation coefficient to be entered is accordingly to be set as less than 1.
Implicit correlations result from the fact that no temperatures, but instead specific enthalpies are used as variables for the solution algorithm. For instance, if one pressure and two temperature measurement points are present on a line, the temperatures are converted in specific enthalpy by using the same pressure. A deviation in the pressure measurement thus has the same effect on both the enthalpy values, which results in an implicit correlation. A special case of an implicit correlation results from the uncertainties in the material value tables. Here, it is assumed as per equation 102 of the guideline VDI 2048 Sheet 1, that unknown systematic deviations arising because of the uncertainties of the material value tables are correlated, if the values of the call parameters lie close to each other.
The third type of correlations between the calculated values (validated measured values and result quantities) arises from the connections in the model, which leads to a coupling via the set process-technical equations via the error propagation law. Thus, in a power plant, there is certainly a correlation between the feed water quantity and the generator power, even when the measurements are totally independent of one another.
Correlations between the different measurement points are considered only when doing an calculation as per VDI 2048. In case of a simple quick-validation, only the diagonals of the covariance matrix are occupied (see Validation Methods). It is recommended to do a comparison according to VDI 2048 when using this method, in order to gain clarity about the quantitative effect of ignoring the correlations on the results. This should be associated with checking the weightage with the Chi^2-test ratio.
The correlations are entered via the dialog "Covariance-Matrix", which is called from the menu "Calculate" à "Correlations":

All the correlation relationships can be entered in these tables. When you click the field "Click to insert item…" in the "Explicit correlations" table, a selection list opens, which displays all the measured values of the model. Select one of these. In the second column, select a measured value correlated with the first one. In the third column specify the correlation coefficient, which must be between –1.0 and 1.0. The symmetric occupation of the covariance matrix is realized through programming. The confirmation for maintaining the condition 105 of the guideline VDI 2048 Sheet 1 (matrix positive semi-definite) results during the calculation.
Implicit correlations can be insert in the "Implicit correlations"-table.
To modify a correlation relationship, click in the corresponding field.
To delete a correlation relation, highlight the corresponding entry by clicking anywhere in the corresponding row, and then press the "Delete" key.
When you close this dialog, all your changes are saved in the model and are used when the validation calculation is done.
Implicit correlations must be entered only between a temperature and its related pressure measurement point. If two temperature measurement points are correlated with the same pressure measurement point, the program automatically takes the correlation of both the related specific enthalpy values into account. However, this mechanism is restricted to only two temperature measurement points. You can proceed as follows, if more than two temperature measurement points are correlated with the same pressure point:
For implicit correlations, the entered correlation coefficient is irrelevant, because this is determined automatically in the calculation. The calculation also takes place automatically for considering the uncertainties in the material tables, as far as this is set in the Validation Parameters. But if the automatic consideration of the uncertainties in the material tables is not set, the correlation coefficient entered here is used.
Result values (validated measured values and other result quantities), which are connected with one another as per the model, are accordingly correlated. In case of a model with 500 pipes, this results in more than 1 million correlation coefficients. With a minimum for the absolute value of the correlation coefficient, which can be specified, only those correlated measurement values are put together for each measured value, whose absolute correlation coefficients exceed the specified minimum.
This list also contains the respective deviation criteria in accordance with equation 141 VDI 2048 sheet 1 and is called by clicking the component measured value with the right mouse button. (Example: last list in the retrofitting example "Calculated correlations of the improvements"). In the results screen (selection with the left mouse button), the index for the measurement value is present on the strongest correlation and the own deviation criterion.
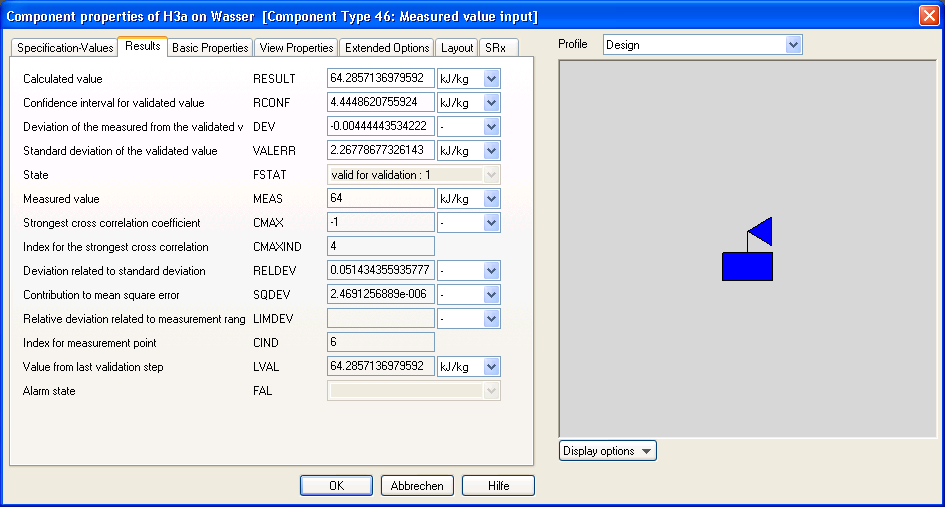
After the validation calculation, whose call is described in the next section, the measurement value screen also contains further calculated quantities along with the validated values.
The value CMAXIND contains an index identifying the measurement point, for which there is the strongest correlation as per the equation 129 of the guideline VDI 2048 sheet 1. The value of the correlation can be found under CMAX. CIND is the index of the measurement point itself.
This figure displays the results of the measurement points with the index as 14. The measurement point 14 is correlated the strongest with the measurement point 16, whereby the correlation coefficient is almost 1.