General Validation Results

The general results can be viewed on the tab "Results" under "Extras"à "Model Options".

There are two entries present at this point: "General" and "Validation".

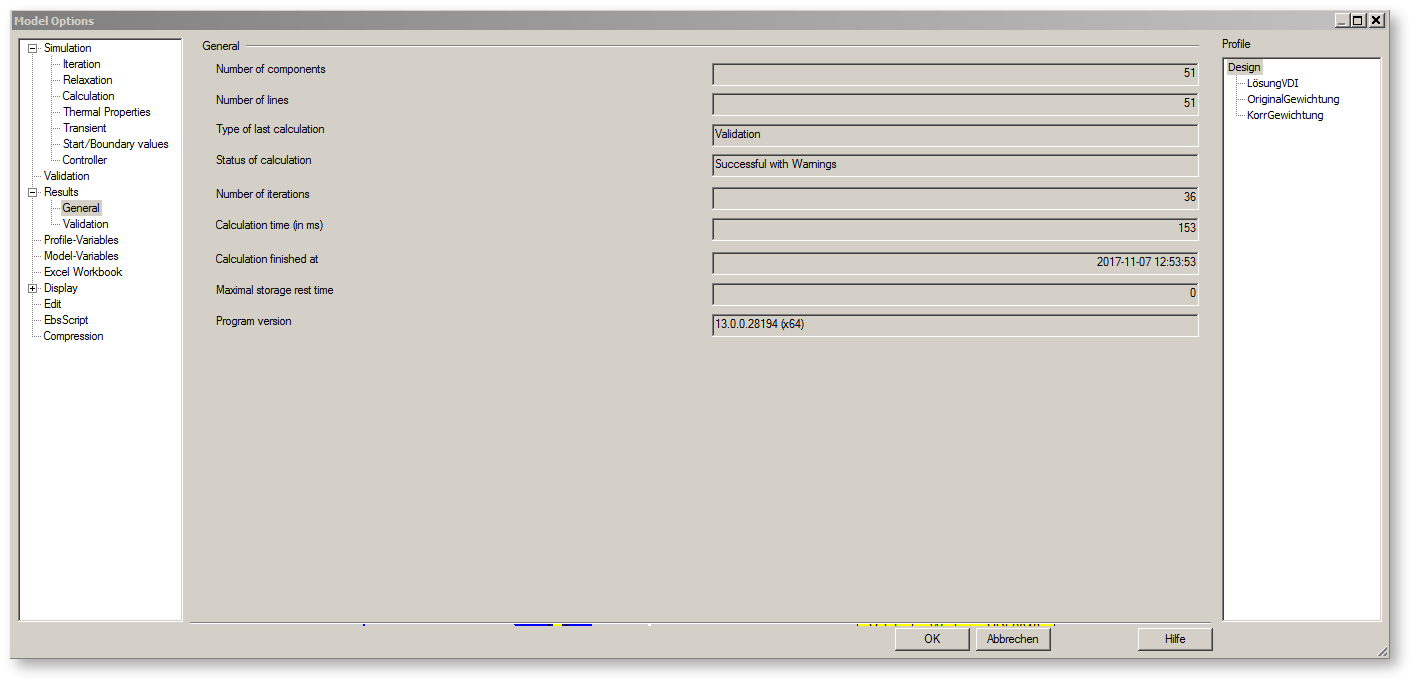
The entry "General" is relevant both for simulation as well as for validation and contains general information about the calculated model, type and status of the calculation and specifications about the time and number of iteration steps.

The result values relevant for the validation are

Mean square error

• This value is a measure of how strongly the measured values deviate from the validated values. These are error square totals, standardized to the number of the degree of freedom according to equation 140 VDI 2048 Sheet 1.

Number of degrees of freedom

• This value specifies the number of redundant measurement points, which are considered in the calculation. It is the same as the number of the non-trivial auxiliary conditions.

Chi^2-test ratio (with reference to mean square error divided by the value of the Fisher-distribution.)

• This value is defined by equation 140 of the guideline VDI 2048 Sheet 1, but both the sides of the condition are referred to the value of the Fisher-distribution. If the Chi^2-test ratio is greater than 1, i.e. if the referred mean square error is greater than the 95%-quantile if the F-distribution, then one or more of the set confidence intervals are doubtful with a probability of 95%, or else model errors are present. The measurement values to be studied violate the condition 141 of the guideline VDI 2048 Sheet 1 and are indicated in the result screens of the measurement values (RELDEV).
  
  Note: 
  The Chi² test ratio is a favoured measure for the consistency of a validation calculation. For each measured value (component 46) its contribution to Chi² is shown as
  result value CHICONTR to facilitate finding the cause of values being too high.
  
• In addition to the Chi^2-test ratio under "Model options” --> "Results” --> "Validation” in case of a validation as per VDI 2048 the relative error square sum is also shown. This is the product of the Chi^2-test ratio and the value of the Fisher-distribution corresponding to the number of the degrees of freedom.

Related sum of square errors

• This value is a measure of how strongly the measured values deviate from the validated ones. It is the error square sum, standardized to the number of the degrees of freedom according to equation. 140 VDI 2048 Sheet 1.

Number of validation steps

• Number of runs, which were necessary for achieving the convergence criterion.

 

The characteristics can also be shown in the text fields in the model. Expressions in the text fields, which are enclosed in braces { }, are used by EBSILON^®Professional for the display. The result values can thereby be accessed through the following expressions:

{@calcoptions.res.type}	Calculation type (1=Simulation, 2=Validation, 3=Optimization)
{@calcoptions.res.status}	Calculation status (0=successful, 1=warnings, 2=not converged, 3=not converged with warnings, 4=error in calculation, 5=error before calculation, 6=general error)
{@calcoptions.res.sqval}	Mean square error
{@calcoptions.res.freigr}	Number of degrees of freedom
{@calcoptions.res.iter}	Number of iteration steps
{@calcoptions.res.time}	Computing time (in milliseconds)
{@calcoptions.res.chi2}	Chi²-test ratio
{@calcoptions.res.valiter}	Number of validation steps
{@calcoptions.res.sumsqerr}	Related sum of square errors
{@calcoptions.res.tolsumsqerr}	Maximum tolerable related sum of square errors
{@calcoptions.res.mintolsumsqerr}	Minimum tolerable related sum of square errors
{@calcoptions.res.valiter}	Number of validation steps

 

To be able to estimate the quality of a reconciliation calculation according to VDI 2048, the relative error sum of squares sumsqerr calculated out of the model is compared to the value of the
95%-quantile of the F-distribution at the corresponding number of degrees of freedom which, according to VDI 2048, represents an upper limit for the plausibility of the confidence intervals.
This value is called tolsumsqerr, the ratio

sumsqerr / tolsumsqerr is called the Chi² test ratio chi2.

If it becomes greater than 1, there are measuring points in the model whose accuracy has been overrated. Their confidence interval must be widened accordingly.

There is also a lower limit for the plausibility of the confidence intervals, as well the 5%-Quantile of the F-distribution minsumsqerr and the corresponding ratio

sumsqerr / minsumsqerr  as chi2min

If this value becomes smaller than 1, measured values are more accurate than assumed. In this case, the confidence intervals can be decreased.