根据拉贝克方法进行的加热器计算

新加热器模型
 

1.  问题描述和动机

用于计算组件 10（FRABEK = 0）的经典方法假设过热蒸汽对传热的影响可以被忽略。

 

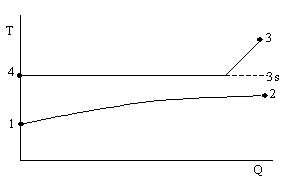
图 1：Q-T-图（经典方法）

 

  1:       进水口

  2:       出水口

  3:       蒸汽进口

  4:       凝结水出口

3s:       压力 P3 的饱和温度

 

所有的计算关系都使用温度 T3 来计算温差。

这种模式有以下缺点：

• 终端温差（T3S - T2）小于 0.5 °C 会导致极高的（k*A）值，并且模拟部分负荷条件时的误差很大。
• 在部分负荷时蒸汽过热的情况下，终端温差的计算并不正确。

2.  建议的解决方案

为了在原则上解决这些问题，必须将加热表面划分为减温区和冷凝区，在部分负荷情况下可以根据热力学条件进行移位。Rabek 在书（G. Rabek; Die Ermittlung der Betriebsverhältnisse von Speisewasservorwärmern bei verschieden Belastungen, Energie und Technik, 1963（不同负荷下给水加热器运行条件的确定, 能源与技术, 1963年））中，发表了一种基于这个思路的计算方法。Ebsilon 中应用了书中的以下几个方面：

• 减温器和冷凝器的模型
• K 比率计算方法

没应用的是：

• 将加热器整合到组件中，因为这种扩展目前没有必要。这类修改可能以后会实施。
• 计算方法和方程的解法。

所用模型的基础是将冷凝区域（I）和过热区域（II）分割开来（图 2）。

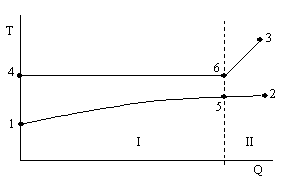
图 2：Q-T 图（新模型）

1:         进水口

2:         出水口

3:         蒸汽进口

4:         凝结水出口

5:         水中间点

6:         蒸汽开始冷凝

I:          冷凝区

II:         减温区

 

以下关系准确描述了传热过程

Q = Q_I + Q_II                                                                                             (1)

Q = k_I A_I Dt_mI + k_II A_II Dt_mII                                                                    (2)

Q:        传递的热量

k:         I 和 II 的 k-比率

A:        面积

Dtm:    对数温差

 

从蒸汽侧的能量平衡中可以得知 QI / QII 的关系，以及对数温度差。所有的温度都可以计算出来。

 

从 (2) 中可以得出

            Q = k_I A_I  Dt_mI (1 + Q_II/Q_I)                                                                     (3)

以及

            Q_I/Q_II = (k_I A_I Dt_mI) / (k_II A_II Dt_mII)                                                          (4)

 

(4) 修改后得到

            A_II/A_I = Q_II /Q_I Dt_mI/Dt_mII k_I/k_II                                                                (5)

总面积为 A，包括

            A = A_I + A_II = A_I (1 + A_II/A_I)                                                                  (6)

或

            A_I = A / (1 + A_II/A_I)                                                                                (7)

 

根据（2），传递的热量可以写为

            Q = (k_IA) / (1+A_II/A_I) (1+Q_II/Q_I) Dt_mI                                                    (8)

 

(k_I A) 代表已知量 WTKF; Q_II/Q_I 来自热平衡。

蒸汽和 A_II / A_I 可以从 (5) 中确定。

为了能够使用方程 (8) 来计算

            - k_I    以及

            - k_I / k_II

必须得出全负荷和部分负荷的关系。

 

为了得到这些关系，再次使用拉贝克术语。

            k_I / k_Iv = (1/a_1v+ 1/a_3v) / (1/a₁+ 1/a₃)                                                (9)

            a₁: a-比率 水（管道 1）

            a₃: a-比率 蒸汽（管道 3）

            指数 v：满负荷

            其中

            b= a_1v/ a_3v         和                                                                               (10)

            g1 = a1 / a1v         以及                                                                       (11)

            g₃= g₃/ a_3v                                                                                            (12)

           结果是

            k_I/k_Iv = g₃(1+b) / (g₃/g₁+b)                                                                     (13)

k - 数比率 k_I / k_II 可以表述如下。

            k_I/k_II = k_Iv/k_IIv k_I/k_Iv 1/(k_II/k_IIv)                                                                 (14)

其中 (10) 和 (11) 得到

            k_Iv/k_IIv = (a1_IIv /a1_Iv) (1+b_II) / (1+b_I)                                                     (15)

a₁- 数的比率可以设置为 u1。

以下适用于比率 k_I / k_IV 和 k_II / k_IIV

            k_I/k_Iv = g_1I(1+b_I) / (1+g_1I/ g_3Ib_I)                                                             (16)

            k_II/k_IIv = g_1II(1+b_II) / (1+g_1II/g_3IIb₂)                                                         (17)

其中 g1I »g1II（同一介质）和 g1II »g3II（单相介质）

适用于

            k_I/k_II = (1+bII) / (1+bI) (1+bI) / (1+g1I/g3I bI)                                           (18)

g- 依赖性取自 Rabek。

            g_1I= (m_1I/m_1vI)^0,8                                                                                   (19)

            g3I = (m_3I/m_3vI)^0,33                                                                                 (20)

通过 (18) 到 (20)，系统得解。

 

3.  计算

满负荷计算（Load = 0，IFAL = 0）是基于终端温差的假设（也可能是负的），由于数值原因，终端温差被限制在 -10K。通过指定这个终端温差，所有的温度都被计算出来。AII / AI (5)以及 QII / QI 被计算出来。根据传热关系（8）和每种流体的两个平衡，可以确定质量流量 m3 和 kI x A。

对于给定的 k_I·A 和 m3 的部分负荷，使用方程（15）和（18）-（20），所有的温度都被计算出来。

传热面积 A_I（冷凝器）和 A_II（过热器）在总面积 A 不变的情况下，可以根据热力学条件进行转移。

 

4.  应用

为了使用新模型，必须在定义菜单中修改一个控制变量。

根据 Rabek 的部分负荷函数

 

1.  K-数 - 比率

k/k₀ = (1/a₁₀+ 1/a₃₀) / (1/a₁+ 1/a₃) = (1 + (a₁₀/a₃₀)) / ((a₁₀/a₁) + (a₁₀/a₃₀) (a₃₀/a))

其中

            a₁₀/a₃₀= b

            a₁/a₁₀= g₁   ;   a₃/a₃₀= g₃

 

k/k₀ = (1+b) / (1/g₁+ b/g₃)

k/k₀ = g₃(1 + b) / ((g₃/g₁) + b)                                                                          (21)

 

2.  减温器/蒸发器的 k-数

k_I/k_II = k_v/k_E = k_v0/k_E0  k_v/k_v0  1/(k_E/k_E0)

k_v0/k_E0 = (1/a_1E+ 1/a_3E) / (1/a_1v+ 1/a_3v) = a_1E/a_1v(1 + b_E) / (1 + b_v)                       (22)

(k_v/k_v0) (1/(k_E/k_E0) = g₁(1 + b_v) (1 + (g₁b_E/g₃)) / (1 + (g₁b_v/g₃)) g₁(1+b_E)

                                =  (1 + b_v) / (1 + (g₁b_v/g₃))                                                (23)

k_I/k_II = k_v/k_E = (1+b_E) / (1+b_v) (1+b_v) / (1+(g₁b_v/g₃))                                            (24)

 

3.  根据 Rabek 的典型值

g3 ~(m₃/m₀₃)^0,33    and   m₃/m₁ ~m₃₀/m₁₀

g₁ ~(m₁/m₀₁)^0,8

b_E~15

b_v~2

从 (1)          k/k₀ = (m₃/m₃₀)^0,33   3/((m₃/m_v)^-0,5 + 2)                                                (25)

从 (4)          k_I/k_II = k_v/k_E = 16/3 (1+2) / (1+ (m₃/m₃₀)^0,5  2)                                     (26)