

|
管道连接 |
|
|
该组件允许指定和计算一个或几个风力发电机的相关风况数据(组件 143)。
风力发电机组的输出功率 P 、轮毂高度上不受干扰风速 v1 和功率系数 cP 之间的关系如下:
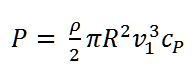
对于现代风力发电机,轮毂高度通常在 100 米或更高。由于处于规划阶段的电厂无法获得轮毂高度的未受干扰的风速 v1 测量值,因此是根据现有的数据(主要是 10 米高度的测量值,平均数为几年)进行计算的。图 1 显示了对数垂直速度曲线的示意图和不同的高度与风速值之间的相关性。
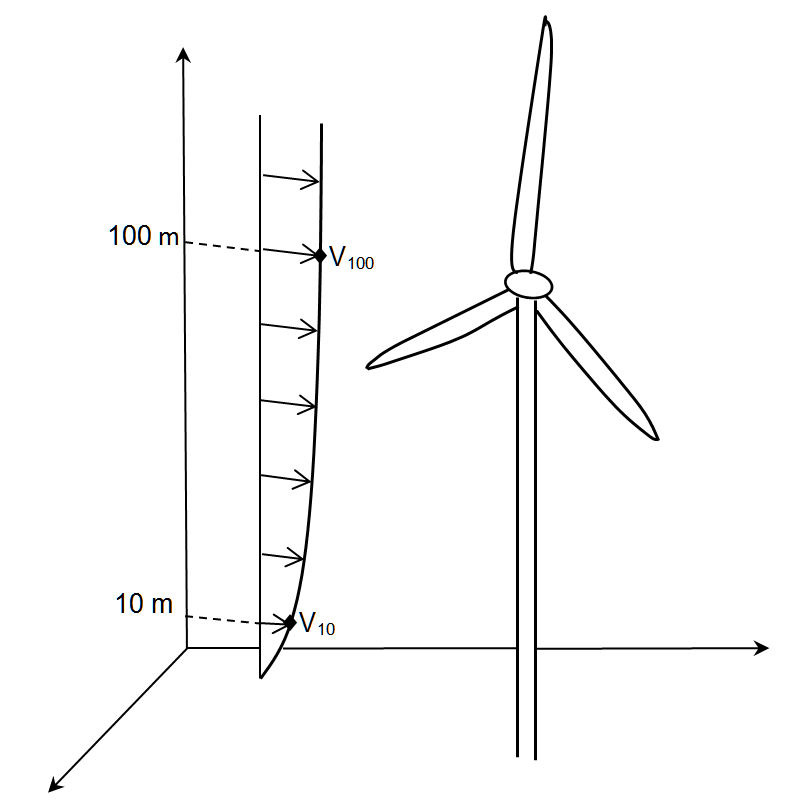
图 1:假设普朗特尔(Prandtl)边界层的对数垂直速度曲线示意图
轮毂高度的风速计算可以根据各种计算算法进行。最简单的方法是基于对数垂直风速曲线的假设(普朗特尔边界层,见图 1)。复杂的算法另外考虑了大气稳定性的影响。这种影响与地面附近空气的垂直温度曲线有关。这里区分了三类情况(见图 2)。在不稳定层的情况下,靠近地面的空气比上面的空气要暖和(典型的夏季月份,地面被强烈加热)。在稳定层的情况下,地面的空气温度低于上面的层(典型的冬季月份,地面明显降温)。在中性分层的情况下,靠近地面的空气层既没有升温也没有降温。为了考虑大气稳定性的影响,需要季节的数据、太阳的位置和云层覆盖数据等。由于这些数据是一个地点的特征,因此只需在一个组件 142 中进行计算,然后将其用于风电场的每台风机。
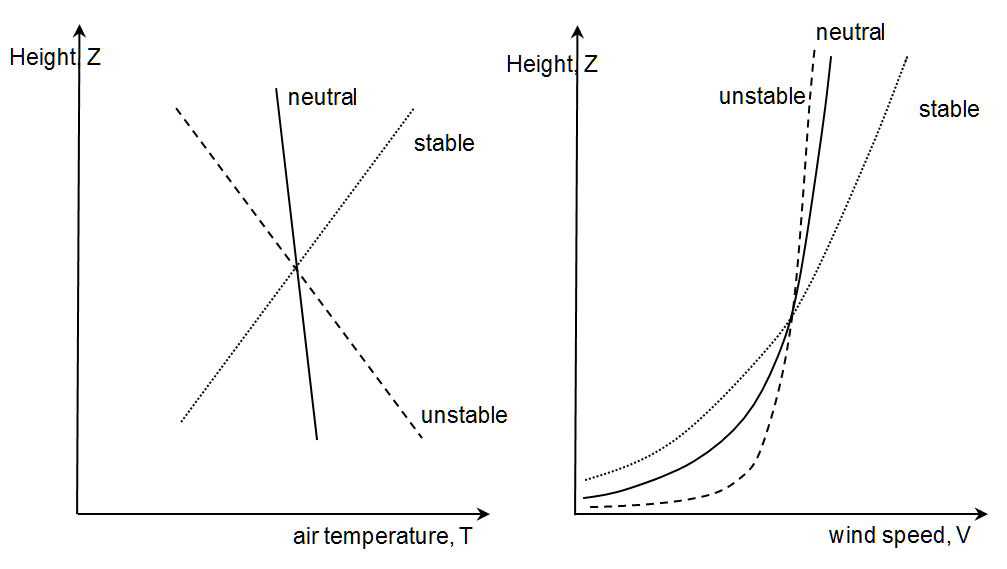
图 2:取决于大气稳定性的垂直温度曲线(左)和相应的风速曲线(右)
轮毂高度的风速计算
算法1:假设两个高度 z1(已知相应风速 v1 的参考高度)和 z2(轮毂高度)位于边界层中,不考虑大气稳定性(或中性分层)的计算(图 1)。
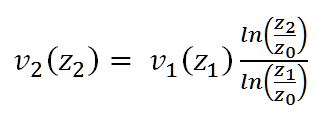
这里用粗糙长度 z0, 高度 z1 和 z2, 以及风速 v1 作为输入。其结果是风速 v2。
算法 2:算法 1 的改进,考虑了大气的稳定性。
额外的输入是以八分量、月和一天中的时间为单位的总云量,从中确定太阳的位置和相应的日出和日落时间。前面的公式由一个经验稳定性函数 Ψ 扩展如下:
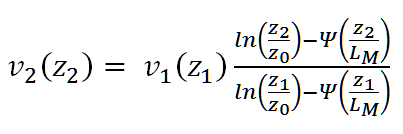
稳定性函数 Ψ 取决于所谓的莫宁-奥布霍夫(Monin-Obukhov)长度 LM,并通过相应的温度分层对风速分布进行修正。稳定性函数 Ψ 的精确形式可以在[2]中找到。莫宁-奥布霍夫长度 LM 可以根据地面粗糙度长度 z0 和 Klug/Manier 的分散类别来确定,根据[3]中的表 17。Klug/Manier 的分散类别又取决于 10 米高度的风速、八分量的总云量和太阳的位置(季节、夜间小时、白天小时、日出/日落前后小时)。根据 Klug/Manier,使用[3](附录A)中描述的算法来确定分散类别。
[1] 建议粗糙度长度 z0 的数值如下:
| z0 [米] | 地区类型 |
| 2 | 城市中心 |
| 1.5 | 郊区 |
| 0.3-1.6 | 森林 |
| 0.1 | 灌木和树木稀少的荒野 |
| 0.03 | 农田 |
| 0.0001-0.001 | 安静的水面 |
在组件 142 中,莫宁-奥布霍夫长度 LM 可以由用户直接指定,也可以在 [3]-[4] 的基础上计算。然后,组件142中的莫宁-奥布霍夫长度可用于组件 143,来根据 [2] 计算轮毂高度的风速。
根据 Klug/Manier 的分散类别和粗糙度长度 z0 ,用于确定莫宁-奥布霍夫长度 LM 的 [3] 中表格 17 如下
| 显示类别 |
粗燥度长度 z0 [米] |
||||||||
| 根据 Klug/Manier | 0.01 | 0.02 | 0.05 | 0.1 | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 |
| I (非常稳定) | 7 | 9 | 13 | 17 | 24 | 40 | 65 | 90 | 118 |
| II (稳定) | 25 | 31 | 44 | 60 | 83 | 139 | 223 | 310 | 406 |
| III/1 (中性) | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 |
| III/2 (中性) | -25 | -32 | -45 | -60 | -81 | -130 | -196 | -260 | -326 |
| IV (不稳定) | -10 | -13 | -19 | -25 | -34 | -55 | -83 | -110 | -137 |
| V (非常不稳定) | -4 | -5 | -7 | -10 | -14 | -22 | -34 | -45 | -56 |
地点的地理位置是从组件 117(太阳)接管的。这同样适用于使用时间序列对话框计算时的时间规格。由此根据 [4],太阳的位置和根据 Klug/Manier 的分散类别被确定。
由于在组件 143(风力发电机)中,制造商的功率特征是指根据 IEC 61400-12-1 规范化的风速,因此有必要知道根据 IEC 61400-12-1 规范化所需的空气温度和空气压力。这些数值对风电场的所有风机也都是一样的,因此它们在一个组件 142 中指定。
参考文献
[1] 风力发电机。基本原理、设计、规划和操作。R. Gasch, J. Twele 第 8 版(德语)。(Windkraftanlagen. Grundlagen, Entwurf, Planung und Betrieb. R. Gasch, J. Twele 8 Auflage (in German))
[2] VDI 3783 第 8 页: 环境气象学--由测量数据支持的分散模型的湍流参数(VDI 3783 Blatt 8: Environmental meteorology – Turbulence parameters for dispersion models supported by measurement data (In German: Umweltmeteorologie Messwertgestützte Turbulenzparametrisierung für Ausbreitungsmodelle))
[3] 《空气质量控制技术指南》--TA Luft 2002(德语)。(Technische Anleitung zur Reinhaltung der Luft – TA Luft 2002 (In German))
[4] VDI 3782 第 1 页: 用于空气质量管理计划的高斯烟羽模型(VDI 3782 Blatt 1: Environmental meteorology - Atmospheric dispersion models Gaussian plume modelfor air quality management (In German: Umweltmeteorologie Atmosphärische Ausbreitungsmodelle. Gauß’sches Fahnenmodell für Pläne zur Luftreinhaltung))
|
ISUN |
太阳能数据参数的指数标号(组件 117) |
|
IWDATA |
风况数据参数的指数标号(当前组件 142,用于在组件 143 中使用) |
|
VWIND |
风速 |
|
AWIND |
风向(从南到北=0°,东向为正) |
|
HVWIND |
VWIND 的高度规格 |
|
CLCOVE |
云层覆盖率,单位:oktas |
|
VWIND10M |
10 米高度的风速 |
|
FLMO |
莫宁-奥布霍夫(Monin-Obukhov)长度处理 =0: 根据 TA Luft, VDI 3782 Bl. 1 和 VDI 3783 Bl. 8 计算,从地理位置(ISUN)、CLCOVE、VWIND10M、Z0 计算 =1: 由 LMO 直接指定 |
|
LMO |
莫宁-奥布霍夫(Monin-Obukhov)长度 |
|
PREF |
参考空气压力 |
|
TREF |
参考空气温度 |
|
Z0 |
粗糙长度 |
|
RLMO |
计算出的莫宁-奥布霍夫长度 |
|
DISPCAT |
根据 Klug-Manier 的分散类别(见上面的莫宁-奥布霍夫长度表) |
 |
显示选项 1 |
点击 >> 组件 142 示例 << 加载示例。